I tried something different now. While it's not as beautiful as ztanz, it's not too far away of that in my opinion:
First, I tried to do a logistic growth Mset. Not too interesting. The graph already made that to be expected.
Then I found out, that certain logistic growths simplify to 1+tanh(z) - still not interesting, but the connection to tanh(z) made me even more curious about the results. - It now seems like tanh(z) is in a way the base of any logistic growth.
Then I thought: Hmmm: this thing actually looks like an integral. It's how many individuals exist per timestep.
So, my next idea was, to take the differential of tanh(z) which is sech²(z). - It's basically how many individuals become added in that certain time-step.
So that's what I'm rendering right now. - The anti-buddhabrot version for now.
It looks very nice and promising. Still quite noisy though. 1/sin(iz)² - I just renormed it a little bit so that the integral over the total set gives 1 but that shouldn't change too much. In theory, that curve now could be used as a probabillity function, at least over the reals

So, the actual formula I'm using is

with a being any positive real - they will always produce 1 as an integral. The specific value of a, I chose, was

, as that made it more symmetric... (2/sqrt(2) = sqrt(2))
Probably, you could directly use sech²(z) for nice results, too. The image shouldn't vary too much...
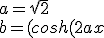+cos(2 a y))^2<br />c=\sin(a y) \sinh(a x)<br />d=\cos(a y) \cosh(a x)<br /><br />xnew=2 a (d^2-c^2)/b+x0<br />ynew=-{4 a c d\over b}+y0)
Oh, btw, I also tried the exiting orbit version. It looked nice as well but cleared up very slowly...
There surely are good reasons for using the gaussean normal distribution but the sech(x)² shares the property of the simple integral and on the imaginaryaxis it's pretty much like a cyclic version of the normal distribution... Looking at the general normal distrubution with sigma and µ, I think it would be very trivial to add that to the sech distribution aswell...
EDIT: Ok, found. It's actually called Logistic distribution (d'uh)
http://en.wikipedia.org/wiki/Logistic_distributionEDIT:
Argh! As usual: Errors make beauty. I missed an h, turning sinh to sin. Now I have to check, wether it still looks as nice, without the error...
EDIT:
Lucky: It changed shape quite a bit, but it still looks interesting

(Hyper short rendertime 'till now - just a few secs... But it already looks reasonable) - certain features still are more or less unaltered, actually...
If you want to look at the error, just use the above mentioned formulae but change the line
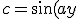 \sinh(a x))
to
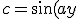 \sin(a x))


















