Tglad
Fractal Molossus
 
Posts: 703

|
 |
« on: October 09, 2010, 03:34:38 AM » |
|
Hi everyone, I decided it would be a good idea to try and categorise 3d fractals. I know there are types, such as menger sponge, but what are the different possibilities and can they be grouped? So I made a list of all the symmetric fractals of a 3x3x3 cube, there are 81 fractals, then I tried naming and grouping them, what do you think of the names and groups? You can change and correct them here https://docs.google.com/document/edit?id=1bz0d4RZ9sg_MKJ-3CsIrLxbYUtYOTjKrGLqhsvq3nxE&authkey=COPg2ho&hl=en#[The cefm codes stand for the eight corner cubes (c), twelve edge cubes (e), six face cubes (f) and single middle cube (m). And the trinary number (such as 1201) is whether each cube (cefm) is either outside the set (0), inside the set (2) or is recursed (moved to the middle and scaled by 3).] |
|
|
« Last Edit: October 09, 2010, 03:40:43 AM by Tglad »
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #1 on: October 09, 2010, 10:36:41 PM » |
|
Nice initiative. This also make me ask how to give a name to a (an hybrid) fractal? I think that, for the realm of 3D fractals, the shortest name would be the generating algorithm (or a representation of it). Reminds me a little bit the story of carbon-based compounds naming  . Is the "ternary code" a representation of the generating algorithm? |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #2 on: October 10, 2010, 02:34:23 AM » |
|
Thanks knighty, yes the ternary code defines how it was generated, its described a little better in the link. What I want to do is to group the fractals and so name each class based on the way it self connects. For example, a tree fractal may look like the mandelbrot set, or a tree or a fern, but it just classed as 'tree'. A bit like topology where a cup and a donut are both just toruses. So each hybrid would also fit into one of these classes. An interesting fractal in the list is 0111, below. I call it a shell and it is like branching planes. Its shape seems naturally stiff, and with some thought it looks like it encases a tree shape, it would also hold water. Any animal that is tree-like in its topology could protect itself in a 'shell' fractal.. but not necessarily this particular one  |
|
|
« Last Edit: October 10, 2010, 02:45:04 AM by Tglad »
|
 Logged
Logged
|
|
|
|
|
Thunderwave
Guest
|
 |
« Reply #3 on: October 10, 2010, 04:33:30 AM » |
|
That's my favorite Fractal. I did hand drawings of this (2d), also with apophysis, and Photoshop. I was going to do this with Mandelbulb3D as well but you beat me to it. It's just a julia set pushed down on the x-axis right, or was that the y-axis?
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
|
Thunderwave
Guest
|
 |
« Reply #5 on: October 10, 2010, 08:51:33 PM » |
|
NICE!  Can I get the code to that? Please!  I'll give you credit, I just want to mess with it and see what I can get it to look like my other ones like this. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
matsoljare
|
 |
« Reply #6 on: October 10, 2010, 09:13:49 PM » |
|
Where are there high resolution versions of the other ones on the chart? And what about the asymmetrical cubes?
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #7 on: October 10, 2010, 09:25:57 PM » |
|
NICE!  Can I get the code to that? Please!  I'll give you credit, I just want to mess with it and see what I can get it to look like my other ones like this. I'm sorry. I didn't save that code. It will be difficult to remind because it was a year ago. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Thunderwave
Guest
|
 |
« Reply #8 on: October 10, 2010, 09:42:38 PM » |
|
NICE!  Can I get the code to that? Please!  I'll give you credit, I just want to mess with it and see what I can get it to look like my other ones like this. I'm sorry. I didn't save that code. It will be difficult to remind because it was a year ago. No problem, it just means I need to try and find it. Thanks anyways. |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #9 on: October 11, 2010, 01:43:11 AM » |
|
Nice render Buddhi, I hadn't ever seen that fractal before. It definitely isn't a tree, and it isn't a sponge, it is in its own class of fractals, which seem to be rarely seen in fractal renders. There is one example in http://en.wikipedia.org/wiki/List_of_fractals_by_Hausdorff_dimension the 3d greek cross fractal which is also a 'shell' (let me know if there's a better name). A good natural example is cracks in rocks. 2d cracks are trees, but 3d cracks are not, they're usually fractal planes. The tree is actually the rock which is cracked. A walnut is a 'tree' since the main lump is composed of 2 lumps, which are composed of many lumps. So the nutshell is a 'shell' as it encases a tree, and holds water. The containing volume of the seashell below is a spiral which is a unary tree with each child segment rotated and connected by the tubes. So the seashell itself encases a 'tree' fractal, so is a 'shell' fractal. |
|
|
« Last Edit: October 11, 2010, 01:55:33 AM by Tglad »
|
 Logged
Logged
|
|
|
|
|
Thunderwave
Guest
|
 |
« Reply #10 on: October 11, 2010, 04:08:39 AM » |
|
It's a 3D version of these styles( Vicsek fractal maybe) that I have produced: Though my way was by crossing lines. The bottom one was by Apophysis which was done by shifting a julia set down the axis.  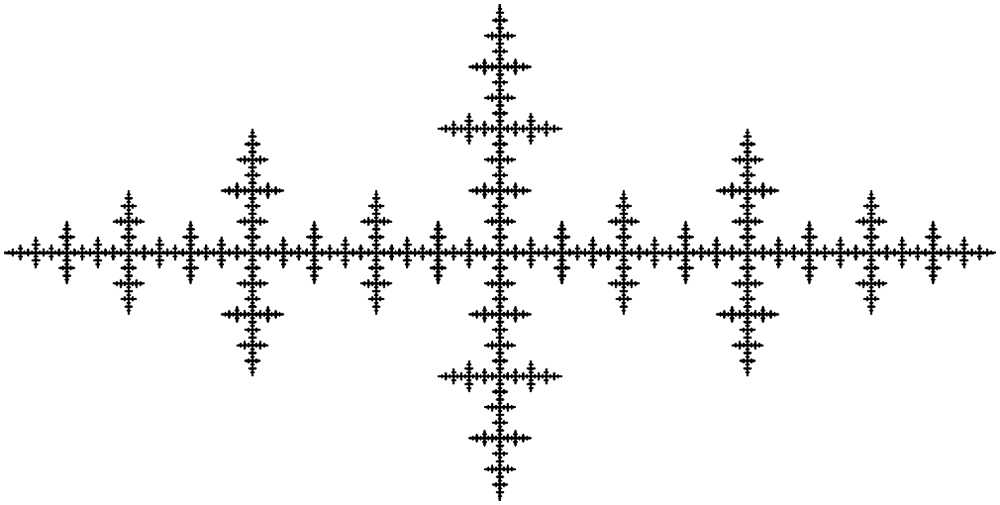 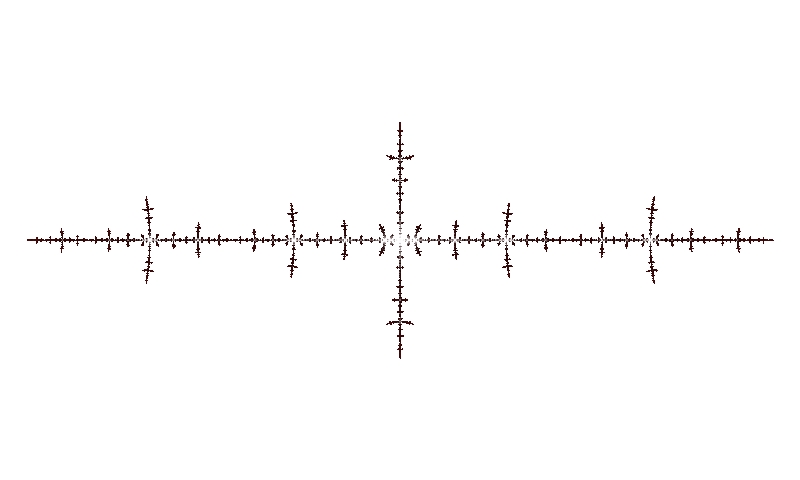 |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #11 on: October 12, 2010, 02:20:19 AM » |
|
@matsoljare- on the link you can copy and paste the images outside the table and enlarge them, only low quality 320x320 though. I only looked at symmetrical to get an idea of the basic flavours of fractal you get from rules on edge,corner,faces and middle, keeps it simple.
@thunderwave- nice image will you post your 3d version on the gallery?
So back to classes of fractal, there is another class you can see from the table (#39, 53, 77) which is almost never seen in fractal renders, it is the 'foam' fractal which is like lots of bubbles, or a solid with fractal air pockets in it. So it doesn't absorb water like a sponge, it doesn't hold water like a shell, but is airtight.
Like the other classes, the thin version has no volume (like soap foam), the normal version has volume (like pumice stone maybe) and the fat version it solid but containing fractal dots (cantor dust) inside; the air pockets have radius 0.
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #12 on: October 12, 2010, 03:00:35 AM » |
|
So here it is, my categorisation of fractals  Each image is a single example for each class. How does the vocabulary sound? I think it covers all 81 types in the 3x3x3 table and covers those in http://en.wikipedia.org/wiki/List_of_fractals_by_Hausdorff_dimension, so you can help me proof it by giving me a fractal and I'll see if it fits  |
|
|
|
« Last Edit: October 12, 2010, 03:02:10 AM by Tglad »
|
 Logged
Logged
|
|
|
|
|
Thunderwave
Guest
|
 |
« Reply #13 on: October 12, 2010, 07:06:39 AM » |
|
@thunderwave- nice image will you post your 3d version on the gallery?
This is the same as those pictures and the hand drawn version; I just gave a more interesting perspective on it, made with M3D.  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Prokofiev
|
 |
« Reply #14 on: October 12, 2010, 03:19:53 PM » |
|
Hello Tom, Interresting work.  Correct me if i'm wrong : We have here the Menger sponge (=1100) and the Cantor dust (=1000), right ? With your classification, the Hausdorff dimension is easy to calculate: 1) If cefm includes a "2" then dimH = 3. (It cannot be considered as fractal, by the way). 2) otherwise : dimH = log (8c+12e+6f+m)/ log(3) |
|
|
|
|
 Logged
Logged
|
Sincerely,
Alexis
|
|
|
|


















