Categorising fractals

[Tglad]

Hi Prokofiev, thanks.
 100% correct about the sponge and the dust. Also nice work on the fractal dimension! So thin foam (1110) would have fractal dimension 2.97 about.
 Yes if includes 2 the dimension is 3, and so its volume isn't fractal, but its surface still is. So much like we coloquially call the mandelbrot set a fractal, I'm ok with calling these fractals, even though only part (the boundary) is fractal.
@thunderwave- nice fractal, that comes under 'thin tree'

An even more unusual and bizarre class emerges from the initial table, the fractal 1111. 0 means empty space that things can pass through, 2 means solid volume with a rigid shape, 1 means recurse and represents border points on the final fractal, e.g. a thin tree has no solid, just border points.
So 1111 is like a sea of border points. Like a solid it contains no gaps and has a known volume (27m^3) in this case; but it contains no solid, so nothing that is defined as rigid, like space, solids could move around in it. So to me it seems like a good description of liquid!
(This view works on the assumption that we can 'bend' the fractal freely as long as the measures of the shape don't change; the length of lines, the area of surfaces, the shape of solids etc.)

Such fractals exist elsewhere, all the space filling curves are seas of border points. I call them 'partial solids'.

[Thunderwave]

@thunderwave- nice fractal, that comes under 'thin tree'

Thanks Tglad!
You inspired another fractal from me type I call: "snowflake, fern, tree".

[Prokofiev]

An even more unusual and bizarre class emerges from the initial table, the fractal 1111. 0 means empty space that things can pass through, 2 means solid volume with a rigid shape, 1 means recurse and represents border points on the final fractal, e.g. a thin tree has no solid, just border points.
So 1111 is like a sea of border points. Like a solid it contains no gaps and has a known volume (27m^3) in this case; but it contains no solid, so nothing that is defined as rigid, like space, solids could move around in it. So to me it seems like a good description of liquid!
(This view works on the assumption that we can 'bend' the fractal freely as long as the measures of the shape don't change; the length of lines, the area of surfaces, the shape of solids etc.)

Tom, I don't think 1111 is different from 2222, They both lead to a simple cubic volume.
And if "1" means "recurse", then "1 represents border points on the final fractal" works only if the final fractal has no volume. I think

Other results concerning, this time, volume:
- If cefm contains no zero => volume= 1
- If cefm contains no "2" => volume=0 (except for 1111)
- if cefm contains only "0" and "2" => volume = (8c+12e+6f+m)/27  for the positions of the "2"s
- Who will come up with the right formula for the volume of a fractal containing "0", "1" and "2"s ?

[Prokofiev]

- Who will come up with the right formula for the volume of a fractal containing "0", "1" and "2"s ?

the formula for the volume of a 3x3x3 "cefm set" is :

volume = n_2 / (27 - n_1)

where n_k = 8c_k+12e_k+6f_k+m_k ,
and c_k = 1 if there is a "k" in position "c", otherwise c_k = 0.
In other words, n_k is the number of "k-cubes" (cubes of type k)

Why ? This derives from the fact that:
- the volume of a "1-cube" is 1/27 of the whole set
- the volume of a "2-cube" is 1/27
so v = n_2/27 + v*n_1/27

Some examples, maybe ?
Full solid cube 2222, made of 27 "2-cubes" => n_2 = 27 and n_1=0 => v = 1
Menger Sponge 1100, made of 20 "1-cubes" => n_2 = 0 and n_1 =20 => v= 0
or the composite sponge 1022 (see attached image)=> n_1 = 8 and n_2 = 7 => v=0.3684

note : the volume of the 1111 set cannot be calculated that way, because of the division by zero. (still, its volume is 1)

[Tglad]

Hey that's awesome Alexis, I think I'll add those formulas to the google doc.
I agree that 1111 is a dense volume, but of what? It isn't 2 which we define as a dense volume of rigid solid, or 0 which is a volume of empty space. The inverse of 2222 is 0000 whereas the inverse of 1111 is itself, it is not the opposite of empty, a class of its own I think.
We could equally define 0 as yellow and 2 as red, 1111 is not the same as a volume of red.
The boundary of a 4d object has a volume of border points so it can happen... but I certainly find it all quite puzzling  

@thunderwave, that is a thin sponge, or thin tree if you consider the overlaps to be circumstantial.

So here's a question, which classes of fractal are in this picture? (answer in the gallery   )

[Prokofiev]

Actually, Tom, I think you should try to define your categories precisely in terms of topology. I think it is a good approach.
Here are some basic ideas:
- Connected / disconnected set (totally or not)
- Holes / infinity of holes
- Branches / no branches
- "1 or 2-dimensionnal topology" (Ugly, i am not a specialist of topology, my idea is "tree" or "shell"-like structure). I think, by the way, that a totally disconnected set can be seen as a "0-dimensional topology".
- volume =0 or > 0
and think those criteria also for  
- its boundary and
- its complementary

for example:
- Cluster = disconnected (totally or not?)
- Tree => 1-dimensionnal topology + no holes + branches
- Sponge => 2-D topology + holes + complementary connected
- Shell => 2-D topology + no holes (=> complementary necessairily connected)
- Foam => 2-D topology + holes + complementary disconnected (totally?) => The opposite of the "Cluster"
We could add :
- "Lace" => 1-dimensionnal topology + holes + branches (like the newton fractal)
- "Path" => 1-dimensional topology + no holes + no branches (like the Koch curve)

From "thin" to "fat":
- "Thin" => volume=0
- "Fat" => volume of complementary = 0

That's a nice Topic. I think we could find help somewhere. Surely this thing has been studied before. I'll have a look.

[Rrrola]

I've seen ALL of those types in Mandelboxes with different scales, but couldn't find the 1D ones...

...until I tried partial Julias (update: z_n+1 = z_n + k*z₀, where k=0 for Julia, k=1 for original Mandelbox) and found the missing 1D ferns.
scale=-1.77, k=0.623:

[Tglad]

Nice find! To be clear with my words, the initial table are _types_ of fractal, the 5x5 table are of _classes_ of fractal, with one example fractal type in each.
So sierpinski tetrahedron, menger sponge and 2d newton are different types of fractal, but they are all in the 'thin sponge' class.

I also noticed many classes of fractal in the mandelbox, you're right I don't recall seeing thin trees... yet! It would be interesting to see how many exist in the basic mandelbox formula (where scale and minR can be chosen).

Alexis, I don't know much about topology either, but I have tried looking up fractal categories, and compared to euclidean geometry categorisation is very sparse.. there are type names (menger sponge etc) and methods (escape time, IFS etc) but not much more than that... at least not that I found.

A nice thing about these classes is you don't care about the exact shape, so you can describe the real world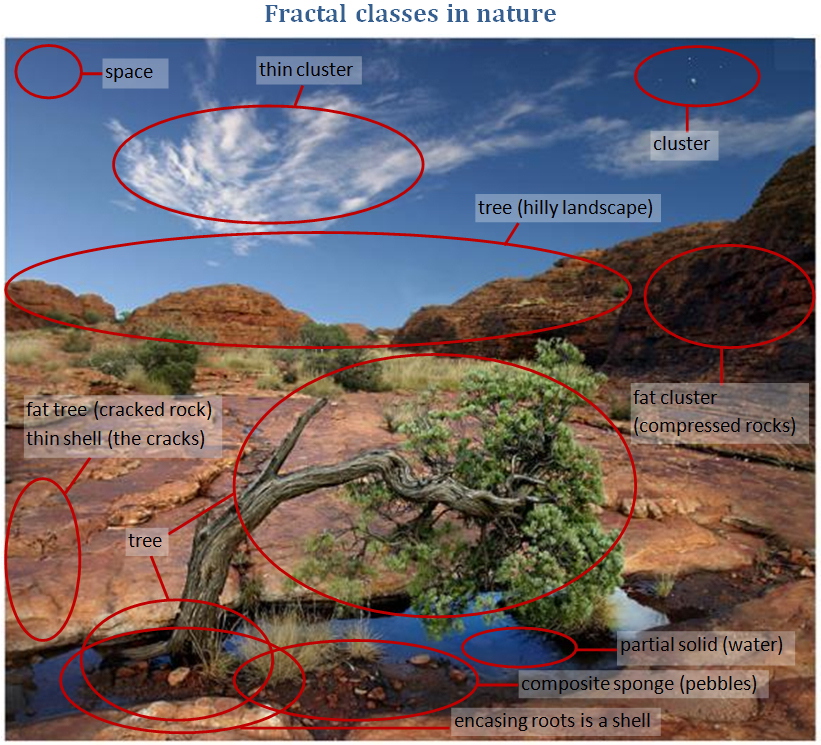


OK, clouds don't look like 3d cantor dust, but if you use a random version and make it denser by removing slices that are smaller, then you get something which varies in density and made of negligeable sized points (water droplets), which describes the structure of clouds well.

The top right is moon and stars, this is a perfect example of a cluster, a few very large spheres (e.g. betelgeuse), many smaller stars, and even more planets, moons, asteroids, rocks etc.

I classified the hills as a tree... this is because the big lump (the world) has smaller lumps on it (big hills) which each have many smaller lumps on them etc. So it is a (normal) tree but with short, wide branches. For a similar reason a solid koch snowflake is a tree, and so a koch curve is a 2d tree border.

[Thunderwave]

So am I getting this right:
Our lungs could be considered a sponge and a shell, like veins (shell or tree or sponge, or all) and the Skin (Sponge or Shell)?  I think so many overlap, like the fern could be a tree.

[Tglad]

A fern fractal (the type) is a tree (the class).
A fern plant is also a tree (the class)
Lungs are complicated things, but I think they are a type of shell, since the bit that isn't lung (the air) is in the shape of a tree.
Veins are trees... ok the viens connect to arteries to form a loop but this only happens once at the largest scale, it isn't fractal loops, so its a tree.
Skin doesn't have a fractal description that I can think of.

[Thunderwave]

A fern fractal (the type) is a tree (the class).
A fern plant is also a tree (the class)
Lungs are complicated things, but I think they are a type of shell, since the bit that isn't lung (the air) is in the shape of a tree.
Veins are trees... ok the viens connect to arteries to form a loop but this only happens once at the largest scale, it isn't fractal loops, so its a tree.
Skin doesn't have a fractal description that I can think of.

Thanks that clarifies a lot for me!

[Tglad]

It took a while but was fun to do, the fractal table with real examples-

hi res https://sites.google.com/site/mandelbox/classes-of-fractal

Can you see the fractal in each image?

[Thunderwave]

Awesome job Tglad!!  I see the fractal in most.  I had to zoom to see the others.

[Tglad]

Now that I have a table of classes we can see how popular different classes of fractal are.
If I google image search '3d fractal', this is how many I find on the first few pages:

	thin	composite	normal	extended	fat
cluster	3	0	2	0	1
tree	3	5	14	0	0
sponge	12	0	0	0	0
shell	0	0	0	0	0
foam	0	0	0	0	0

Partial solid: 0

So we rarely see anything but trees or thin sponges.

Admittedly clusters, foams and 'fat' fractals are perhaps less interesting to render but it looks like shell fractals could be a big uncharted area of interesting shapes.

[Thunderwave]

...it looks like shell fractals could be a big uncharted area of interesting shapes.

Perhaps people already live in a shell....  teehee...   I know I do.

I like the idea of exploring shells though.  Exactly how does one create them?  like this:
?