I posted this material when commenting on an error in the handling of terms
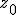
(the initialisation term) and c (the fixed term) in the Mandelbrot/Julia iteration formula given in an
UltraFractal-related thread recently, but as I've seen the error repeated elsewhere I think it's worth a separate thread here...
The same iteration formula is used to determine membership of the Mandelbrot Set and all Julia sets and is usually written in this form (see for example p.161 of The Beauty of Fractals):
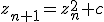
Each point in the complex plane is a 'candidate' for set membership and the iteration formula is applied repeatedly to determine whether it is or is not a set member. If the iterate remains bounded (modulus less than or equal to 2), the point is a member of the set, otherwise (modulus greater than 2) it is not a member.
However, for each set, different initialisation criteria are applied before starting the iteration sequence.
For the Mandelbrot Set:
- c is set to the coordinates of each candidate point.
-
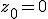
for all candidate points. Hence from the iteration formula, the iteration sequence is
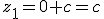
,
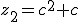
,
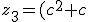^2 + c)
, and so on counting from iteration 1.
For Julia sets:
- A fixed point is chosen from the complex plane. This choice establishes the 'identity' of the Julia set to be calculated.
- c is set to the coordinates of the chosen point and remains fixed for all candidate points and across all iterations for each candidate point.
-
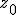
is set to the coordinates of each candidate point.
The consequences of these distinct initialisation criteria are that:
- There is only one Mandelbrot Set.
- There is an infinity of Julia sets, resulting from the free choice of fixed point.
When drawing the sets on a pixel grid, the complex coordinate
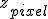
of each pixel is used during initialisation:
- For the Mandelbrot Set,
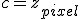
- For Julia sets,
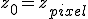
Sometimes, descriptions of how the sets are generated fail to clearly or correctly address some aspect of the above. For example:
- They might clearly state the iteration formula but fail to state the initialisation criteria for
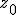
.
- They might treat
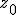
as the fixed term in the iteration formula, whereas the fixed term is actually c and
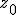
is the initialisation term for the iteration sequence.
Some additional points:
- All the above relates to the quadratic Mandelbrot Set and counterpart Julia sets. Other Mandelbrot sets are possible and are generated using different iteration formulae; in all cases, the
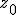
term for the M-Set is initialised to a critical point of the iteration function (which is simply an alternative way to represent the iteration formula). Critical points are where the derivative of the iteration function is zero. For the quadratic M-Set, the iteration function is
 = z^2 + c)
and the derivative is
 = 2z)
. Solving for
 = 2z = 0 )
yields only one critical point (z = 0); other functions may have several critical points, in which case a distinct M-Set can be drawn for each critical point.
- Any practical program for drawing the set will need to apply an iteration limit to prevent an infinite loop for points inside the set. Programs typically allow the iteration limit to be adjusted; to improve the fidelity of the rendering, it will need to be increased when zoomed deep and for certain areas of the fractal.
John.


















