So while the Mandelbrot Formula will add the starting point for each iteration, the Julia Formula will add the same constant regardless where you started off.
The fixed term
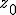
in the Mandelbrot set formula isn't correct. The same iteration formula is used to determine membership of the Mandelbrot Set and all Julia sets and is usually written in this form (see for example p.161 of The Beauty of Fractals):
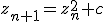
That's equivalent to your Julia formula, but uses a different convention for the subscript numbering.
Each point in the complex plane is a 'candidate' for set membership and the iteration formula is applied repeatedly to determine whether it is or is not a set member. If the iterate remains bounded (modulus less than or equal to 2), the point is a member of the set. However for each set, different initialisation criteria are applied before starting the iteration sequence.
For the Mandelbrot Set:
- c is set to the coordinates of each candidate point.
-
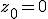
for all candidate points. Hence from the iteration formula
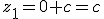
,
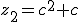
,
^2 + c)
, and so on. So your comment that the starting point is added for each iteration is correct, but it's the result of application of the c term rather than the
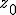
term.
For Julia sets:
- A fixed point is chosen from the complex plane. This choice establishes the 'identity' of the Julia set to be calculated.
- c is set to the coordinates of the chosen point and remains fixed for all candidate points (as you commented) and across all iterations for each candidate point.
-
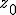
is set to the coordinates of each candidate point.
The consequences of these distinct initialisation criteria are that:
- There is only one Mandelbrot Set.
- There is an infinity of Julia sets, resulting from the free choice of fixed point. As Alef commented, when deeply zoomed in the Mandelbrot Set, small differences in choice of c are likely to result in Julia sets that are visually indistinguishable.
When drawing the sets using a pixel grid, the complex coordinate
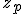
of each pixel is used during initialisation:
- For the Mandelbrot Set,
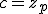
.
- For Julia sets,
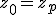
.
Sometimes, descriptions of how the sets are generated fail to clearly address some aspect of the above, e.g. they might clearly state the iteration formula but fail to state the initialisation criteria for
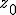
.
John.


















