END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

I missed this lecture in this serie on the continuum concept.

<a href="http://www.youtube.com/v/Y3&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/Y3&rel=1&fs=1&hd=1</a>

<a href="http://www.youtube.com/v/Y3-wqjV6z5E&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/Y3-wqjV6z5E&rel=1&fs=1&hd=1</a>

It is relevant here because the eventual structure for extending the natural / rational numbers is based on a process of modulo or clock arithmetics based on polynomials/ polynumbers. Polynumbers are a fundamental capstone rank array in the Grassmann general sense. In this process we can label the so called complex arithmetics, the finite arithmetics, the arithmetics that require or etc.

Underpinning these processes is the general method and analysis that is Hermanns extending or extensive magnitudes.

I have already mentioned that Hermann does not subscribe to the Dedekind cut or to infinitesimals. His concept is based on extensive and intensive qualities of magnitudes. §7 which I am retranslating touches upon this label or handle for the doctrine of the extending / extensive magnitude.

It should be noted that Newton did not subscribe to infinitesimals despite what you may have heard. If you actually read the Astrological principles as foreworded by Cotes you will read his distancing his method from that of those on the continent, that of Leibniz and Cauchy and others. Newton always used the principle of exhaustion.nhis Fluxions are minuscule assigned values . Thus they always remain Archimedian and pragmatic.

Commentary
On §7

I have at last completed a reworking of this section. If anyone else would care to translate this section and post it I would appreciate it.

This section is perhaps the real heart of Grassmanns Method of analysis and synthesis. Everything leads up to this section which is the foundation of the Ausdehnungslehre.

This is a dance of ideas and notions tracked by labels and label definitions explicit or Implicit.. The reader is by now induced into a trance of new ideas and new relationships , excitedly waiting in anticipation for the great event, or totally confused and alienated!

The great event is the splitting, the hewing and hacking into 4 parts of the thought patterns that underpin the doctrine of the thought patterns. From this one is anticipating a revolution in productivity and thought process in setting describing and solving problems in 3 d space.

Commentary
The Quantum and the bestimmter Kraft begabten Punkt or the exemplar of intensive magnitude.

Clearly intensive magnitude concepts go back to antiquity, but it seems Leubniz and Kant and Hegel are the western proponents of such a concept.

However rather than wade through their weighty tomes it is enough to realise that in section 7 Hermann gives his own , Hegelian inspired take on the subject of intensive and extensive magnitude. The essential point is that in a very few admittedly tersely worded sentences ( especially in the German) he evokes the metaphor of a step rise, or stair step.

Contrast that with the metaphor of an extending line segment and yo get a picture of quantum as the stair step and continuous extension as the line segment.

Quantum as the intensive magnitude can in fact have Any value. In that regard it is continuous and expressible by a line segment. But while a line segment extends beyond its bounds, that being the nature of extension, a stair step is bounded and cannot get beyond a climax.

The climax however is bestimmter which I take to mean assignable, or appointed. Thus Hermann attempts to convey a physical representation or a pragmatic notion of an intensive magnitude. Fix the boundary but vary the density within that boundary. This is a measure of intensity or density that is quantised, yet continuous!

 Ŵhen we consider the Planck constants and the Planck lengths and even the Dedekind cut we have to acknowledge as Hermann says that these concepts are cut continuous ones, like the cutting of of limbs he suggests in the German.

The Ausdehnungsgröße concept allows this quantum concept to be explored in the context of a contiguous combinatorial environment and to be represented spaciometrically by line segmented figures. Thus intensive magnitude can be explored geometrically for new insights. Quanta no longer have to be represented by discrete blocky diagrams but can be explored by Ausdehnungsgröße as combinatorial objects.

This was new and to Hermann a huge advantage of his method .

Mach, Planch, Dirac and others all were heavily influenced by this approach to seemingly discrete or intensive phenomena . Whether they understood and applied Hermann properly is a question for research. I doubt it though , because of course intensive magnitude is not a unique idea to Hermann. His method of dealing with it by Ausdehnungs Größe rather than continuous or real numbers sliced at some assigned value seems to be his though.

Norman again on the Dedekind cut. Compare with Hermanns concept in §7
<a href="http://www.youtube.com/v/4DNlEq0ZrTo&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/4DNlEq0ZrTo&rel=1&fs=1&hd=1</a>

<a href="http://www.youtube.com/v/4DNlEq0ZrTo&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/4DNlEq0ZrTo&rel=1&fs=1&hd=1</a>

Commentary

Rather than pander to the idea that mathematics might be truth, Hermann lags out the psychology of its construction. Thus being limited to space and time for extension, we have to recognise all else a formal works of the imagination. Thus it is important that those theoretical formalisms cohere with the definitions. It is also vital that they are inter communicant with some real confrontational experiences. Only in that process can we dare to say they may be true, but not necessarily the Truth. Especially when the vast majority of what we want to measure is of the intensive magnitudes.

The great impact of Newtons ideals were due to his  careful alignment of them. Following Glilro he starts with undeniable abolutes( although we can now refute the Jovian system description) and by a chain of relations and analogies brought the independence down to earth, to common weights and measures proceedings.

So carefully did he arrange this labelling and proportionately relate them that they survive today As a coherent set of principlesl but they are only man made , not divined from god ?

In particular the imagination to use line segments to represent essentially potential associated with a point. In fact it was something some people were unconsciously doing, but not thinking straight. Hermann points it out as a part of the normal realisation process of thinking in joined up figures.

As a consequence of this distinction examine

AB + BC = AC

This is a combinatorial magnitude, consisting of 2 primitive magnitudes..

Or it is a script written in a certain pattern on a computer screen .

Leaving aside the identification of what it is ( simply, the reader must decide choose aor accept its semantic status) let us contextualise it in Hermanns discovery story. Then A,B,C are points in the plane ( arbitrary). They are glossed as intensive indicators of relative position, but that is not gone into. It is demanded of you to accept them as points of position. The point is given the power or attribute to indicate a spatial position. This is a bestimmte Kraft begabte Punkt!

But then we immediately set that aside , if we ever realised it, because the author hurries us on to an extensive magnitude: the line segment that connects those points. AB is thus an extensive magnitude , and we are happy with that , even if we do not understand or every way stand it!

The three extensive magnitudes are in fact quantised, and the end points set the quanta limits for a line . segment . We are directed to enumerate, evaluate or denote a quantity called the length of this extensive magnitude. In fact we are asked to do this so often that we think that that is what this extensive magnitude Is ! We rarely recognise that we are evaluating an extensive magnitude, because no one thinks it important enough to discuss. It is pushed aside as" elementary", " clear", " trivial" , "obvious" and many many other subjective directions away from what one is Actually doing.

Thus when Hermann directs us to evaluate the direction of AB and the length of AB and to hold them fast and of equal importance , it is not the result of these evaluations he is addressing, but the process of evaluation itself.

If you recall the Wolfram Alpha language you will see just how fundamental this observation and process is. Without this drive to build calculating machines, very much enhanced by the work of Leibniz , and the polynomial or polynumber concept, we would not have ended up with Turing once and for all , presumably, tackling this supposed elementary process.

I could say Hermann tackled it before him, but that would be unjust. Nevertheless Kant,Leibniz,Hegel and Grassmann laid the foundations for the work of Turing, and the work of many others. I would include Hamilton, but his conception is particular and as he acknowledged, an instance of the more general conception of the Ausdehnungslehre.

So now we have the three extensive magnitudes, each having length and direction hovering about them . How do we proceed?

Arithmetically we could add the lengths . We obtain a numbered dimension that supposedly reorients an extension. However, in space it is representing the triangle form.. As an extension this is bounded in the form. The form has a bounded extension we identify as say " area" , but that is not what the three lengths add up to. .

We choose to identify this sum as the perimeter of the form. It is a finite extension with a variation in direction, which forms a closed "loop". That description is itself, precisely an extensive magnitude, Ausdehnungsgröße. The number or numeral 10 say , even 10cm says nothing about this magnitude. In fact it obscures it behind one form: the ruler or measuring stick!

Thus the first realisation is our notational practices are defective! On top of that they are misleading. If I say the circumference of a circle is 3.142 times the radius, I imply that I can straighten out the curve and equate it to a straight line! This I assure you we cannot do physically , nor can we do it formally. This is why Hermann points out that geometry confronts our thinking process, and so cannot be a formal thought reeified system!

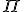
Clearing that up was crucial to his understanding of the Ausdehnungs Größe. But in fact he was only echoing what Eudoxus wrote 2300 years ago: there are different kinds of magnitudes and the ratio ought to be between homogenous magnitudes! Instead we seek as a ratio between non homogenous magnitudes. Is it any wonder that the ratio is transcendental? That word simply means we humans cannot fathom it. God alone can make a curved line straight, for only God can change its essential conceived nature.

Do not be fooled by a piece of string. Rather realise we assign properties and attributes to space like objects at our own convenience. The better we account for the spaces essential nature the better the attributional model we build. Thus using intensive magnitudes as tally marks where an extensive magnitude is required as a lineal combination, is going to lead to conceptual ifficulties in the end,

Now we have ABC as an extensive magnitude, which can be separated into line segment extensive magnitudes. There is a combinatorial reationship that is very very fundamental between these 3 extensive magnitudes

AB + BC = AC

This is not an arithmetic combination, or as Hermann labels it an algebraic combination. Right there he is at odds with the modern notion of Algrbra! In fact that is the issue. His label is pertinent to his time. Algebraic meant symbolic arithmetic, not the many and varied meanings we give it today based on the writings of Hamilton nd Boole.

The statement is a combinatorial expression. Hermann was blessed with the combinatorial teachings his father had penned nd introduced into the Stettin high school system. This paper really does need to be read to understand where Hermann is coming from,

The combination of these 2 extensive magnitudes can be labelled by a third extensive magnitude. However to be a combined extensive a gnitude the 2 parts must be contiguous, so that one can say the combination is indeed an extension from the smaller into the greater.

What if they are not contiguous? No problem, they are dealt with under the discrete doctrine of the thought Patterns and as such they are dealt with as discrete tallie and discrete combinations.

The realm of the continuous provided Hermann with the neglected field of study , the continuos( contiguous) combinatorial magnitudes. These he recognised or denoted as the true or obvious candidates for the label extensive magnitude. To do so he had to identify the continuous uniform magnitude as the continuos algebraic.

Because, he claims every magnitude in that pattern is uniform we can quantise it by a uniform quantum. In so king we can study the quantum, because it is indistinguishable from the entire whole. This is one of the characteristics of an intenive magnitude, it is scale free, uniform and indistinguishable. To istinguish it we have to impose formal quantum . As quanta they are bounded, and cannot extend beyond their bound no matter how contiguous they are!

A little thought will clarify why that condition is imposed by Hermann on intensive magnitude. He does attempt to closely explain it, but my translation may not be clear enough to get that across.

Extensive magnitudes on the other hand grow out of each other. Because they are not uniform in boundary or other characteristics the contiguity is important. For Hermann the concept is tht one segmented part actually extends out of a prior one. So for example. Crystal grows in this manner, and reveals it was thought a Truro aspect of nature: extensive growth of magnitude in any direction with any intensity. The everyway varying magnitude!

Due to the Hegelian logic, Hermann can hold these things together in a combinatorial resolution. Aristotelians would be going absolutely crazy trying to pull them apart!

It is not that Hermann does not pull them apart, because he cn and dies. Rather it is that he can go beyond the snalys to the synthesis and flip between the 2. This is the power of the Hrgelian toolbox.

So finally AC is an extensive magnitude, but it is now Aldo a labell Gordon a combinatory extensive magnitude which is dissectable ( zergliedern) into 2 subordinate ( untergeordnet) extensive magnitudes.

The labelling and the ordering does not stop at this simplest form. We can expand this formula into a vast endless array of such combinations. This is the Reihe that Hemann perceives, and it is fractal.

I have been able to use the expression rank array because today, after do long a time and after Caylry and others pioneering work in establishing a notational system or them, and Clifgord work in establishing the dot nd cross pouch notation from both Grassmann and Hamiltons less apprehensible notation involving the notation we have some familiarity with a rank array. In addition Gauss elimination method crystallises some of the notion of rank. Hermann clearly had these notions in mind as he wrote which is why his original work still resonates today. Back in his day such a system was perhaps only apprehensible by LaGrange LaPlace , Gauss and Euler, but it is their summand notstion tht obscures it fom moden eyes.

The counterpoint to the extensive magnitude is the intensive magnitude( continuous), but what Grassmann points out is the duality tht exists in the notation, resulting in many insights transferring back and forth between the 2 types of magnitude. The two processes are inter communicant!

Finally the notation makes clear what is intensive and what is extensive.
Thus e is an intensive or extensive bound magnitude 5 e is a continuous intensive magnitude.e₅ is the 5th Differring part of a 5 part extensive magnitude which will be
e_I as I runs from 1 to 5.

We can reduce an extensive magnitude to n intensive one by constraining the e_I to being uniform.

There is a lot more besides this, not the least being the product notions associated with extensive magnitudes, which dawned on Hermann, according to the story,when he was looking at geometrical or trigonometrically ormulae fir te area of a rectangle/ parallelogram.,

The final part is the Schwrnkunglehre part, where he finds out about a third kind of product, the roots of unity products of Cotes and De Moivre, as expounded upon by Euler.

Whatever he came across he reworked in line with his growing confidence in his Ausdehnungs Größe concept and his growin apprehension of the intenive and extensive magnitudes and their role in describing or modelling the kinematics of the real " world" .

I want to apply the Ausdehnungslehre or rather the Formenlehre to some physicl phenomena, as Ampère attempted to do. But here is a taster of the standard application to circuits, in which you may experience some confusion as to what the use of vectors is and what the graphs are doing. In fact the mixed ptiduct of this thread is relevant to this description, which I hope will become apparent by and by.

<a href="http://www.youtube.com/v/LEWKHvuRsUk&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/LEWKHvuRsUk&rel=1&fs=1&hd=1</a>
<a href="http://www.youtube.com/v/LEWKHvuRsUk&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/LEWKHvuRsUk&rel=1&fs=1&hd=1</a>

However if you first get clear in your mind what an extensive magnitude is and what an intensive magnitude is , then you might orient yourself to this kind of application( which by the way I think is misleading anyway! But that is beside the point)