Der Ort der Hamilton schen Quaternionen in der Ausdehnungslehre

[jehovajah]

It is worth drawing attention to that the step rise was a label associated with Intensive magnitude particularly. Now the label is being used to denote particular systems at differing levels or stage kinds or step rise types. What is going on?

Simply the intensive magnitude at each stage is of a different kind. So a point on a line is different to a point in a plane, and likewise a point in space. The intensivity of this magnitude is increasing, but extension of this magnitude is not . Hermann called it the empty or emptying magnitude as far as extensivity goes.

To ignore the intensive magnitudes is to diminish the potential of these magnitudes. In particular, when I refer to a circular or spherical intensive magnitude I include within its intensivity its Rotation. Thus a point in space is invested with many crucial but invisible dynamic potentials which physicists may draw upon.

[jehovajah]

Homogenous coordinate systems that  Norman introduces in his universal hyperbolic series, are another construction of these extending magnitude systems, and Norman introduces another for spherical and elliptical geometries in that series.

The Riemann  projection of the complex plane onto the sphere is another extensible magnitude system, and Gauss use of the unit sphere to specify curvature and tangent planes, bundles etc is another application.

In each of Normans presentations he is careful to define or label the different magnitudes. He also utilises the row or column flexibly as he requires it to specify what he wants to distinguish.

Extensive magnitudes doctrine concentrates on the continuos or contiguous extending magnitudes, but Norman has also done work in the discrete magnitudes to bring everything into line in his thinking.

[jehovajah]

Commentary

The simplest rule is identified as direction, or interpreted as direction in space. Actually the word used is Gleicheit. The thing or entity that has the like quality.

So hermanns all encompassing rule that binds together and governs all particular variations  is direction.

Actually this is hard to fathom without realising he is meditating on the line segment label and it's relationship to the endless line notion.

We usually call this a I dimensional space. We could call it an einfach or simplest space which is directly translatable as a "one type " space.

We do not even get to consider the linguistic origin of this notion, the linguistic label, because as mathematicians , early on we are indoctrinated with the idea that the straight line is the simplest line that we can "draw" or rather draw upon for insight and geometrical construction.

In fact Euclid never said that. Very much in line with Hetmanns approach he isolates the straight line as having unusual specific properties in line with the ideas of indicators or seemeia, usually translated as" point", but as we have seen that is an interpretation of an intensive magnitude experience.( according to Hetmann).

I have translated the Greek Isos as " dual" for a number of years now, because of meditating on the idea of a point for most of my life! In that regard a "good" line is made up of dual points, not just the points on the beginning and end. And a line is any scratch or dragged mark! So Euclid identified a good line as one particular sort amongst any number of sorts of drawn lines including curved , crazy and scribbled lines.

I proposed that the progenitor of these notions was in fact the circular line, and that the dual point was the intersection of 2 circular arcs. In this proposal the easiest line to draw is a circle not a straight line.mthis is because mechanically it is easier to draw a circle than to create a ruler or a piece of twine to reify the concept of a straight line.

In any case Hermann has adopted the common belief that a straight line is the simplest mathematical/ geometrical magnitude and drawn his all encompassing rule of direction from this premise.

Needless to say I do not agree with this characterisation, but the general rule he formalises is a very clever and serviceable one. It in fact allows for any all encompassing rule that is one type. Of all the possible one types, including spiral arc segments the circle is profoundly the most useful and magical ! It marks a conception that defines a plane from 2 intersecting spheres. It can be elaborated more, but I do not have time now.

Hermanns all encompassing rule therefore is : any variation whatsoever must maintain the initial direction. This is what he is indicating with a,b,c. These extensive magnitude variations whatever they may be all have the same direction by this rule.

There are issues with this assertion of a rule of direction, which I will wait to see how Hermann sorts them out.

[jehovajah]

I have corrected some typos in the course of grappling with §11, and updated the commentary.

The point is that Hermann is formally expositing an n- directional system accountable by the doctrine of extending magnitudes.
The problem of language labels looms large. It is clear and important to realise that Hermann relies upon clear language descriptors to distinguish each notion. Thus each label or handle is specified to a task or distinction. So extending magnitudes are not the same as extending an algebraic system from a binomial to a trinomial to a 4 term etc system. In fact coordinate systems as an accounting method were ill explored prior to Hermann. This mix up was due to making geometry a formal system.mthat blocked any further insight into formal systems and their development.

It is clear that Hermann identified direction as his fundamental Rule/Law governing each elemental extensive magnitude. The exemplar of such an elemental is in his system a straight line segment. Thus every variation in a line segment obeys a fundamental " law" for that specific line segment: vary only in the direction of that line segment!

As builders of systems that gives us endless possible directions to choose from, not just 3!

So why was 3 so important ? Well it was not, but orthogonality in circles is very useful and universal. However an orthogonal pair of diameters is not so easy to construct. Thus when Thales theorem, so called, was discovered in the far history of Egypt and Mesopotamia and the Indus Valkey civilisations it was a big deal.

I say it was not important only in the context of formal systems. In geometrical and spaciometric construction systems it is one of the fundamental postulates, aitema, that a student has to demonstrate to get accepted onto a Pythagorean scholarship. Thales theorem for right angles is a construction all Stoikeia students have to demonstrate along with about 4 others.

However, in space there is no direction that is the foundation of all others. We do not even have language to identify uch a concept properly. In fact arbitrary or whimsical is the only way we can describe any such protagonist!. But as soon as we choose one we become locked into an system that is constrained by orthogonal constructions. 3 dimensions is not an absolute general property of space, but it has to be realised in any and every system we may adopt. So any n dimensionl or rather n- directional system( and the distinction is important) must be able to generate an orthogonal system within its structure.

This is not the same as saying that there are only 3 directions in real space, or that space is 3 dimnsional. It is precisely saying any n directionl space can construct 3 orthogonal directions arbitrarily.

This is crucial o the topic of this thread. Rotation can be understood as transforming from one 3 directional orthogonal system to any differing 3 directional orthogonal system. But further still rotation can be understood as transforming from one n-directional  system to any other n- directional system.

We cannot apprehend rotation , formally, if we change the structure or step of the system.

Hermann uses 2nd and 3rd step or stage or level to denote the Intrnivity of the system. The intensivity is the Account Tally of the system. It directly accounts for how many stages one has to go through to identify a singular or unique element of the system called a Point or a reference Point. The concept of a point is thereby assigned n Intensity magnitude. It occupies no extensive magnitude, rather it characterises the intrinsic nature of the extensive space. It denotes how much processing we have to do to apprehend this singular " point".

In terms of intensive magnitude , this concept is a very interesting interpretation.Nto look at a colour and distinguish its intensity requires several layers of subconscious processing, never mind the unconscious processing that underpins those layers! Thus layers , levels or stages in a processing activity well model the experience of an intensive magnitude. The fact is these processing layers may occur in parall, rather than sequentially only interacting at a given " point" ( or arbitrary point) in the processes to give the final outcome or evaluation/ experience.

In addition to parallel processing add incredible " speed" of execution and you may apprehend why our computers have become excellent models of our own subliminal processing resulting in qualitative experiences.

Nevertheless to model these intensive experiences by extensive magnitudes can lead to interpretative confusion. Hermann resolves this by denoting direction as one interpretation of the rule / law of Varying!

As I pointed out earlier, one is held in a hypnogogic state where word salads come at you with hardly ant semantic referent, hardly any meaning in a specific concrete object. Thus when supplied with a concrete idea, or st least a familiar one , the mind clings on to it for dear life! In so doing it forgets the more general vague motion which it replaced by it. However, when certain boundaries arise because of the specific nature one has accepted the vague notions once again become serviceable as a means of hopping over the boundar into an analogous interpretation. Thus , using extensive magnitudes to model intensive ones does not confine us to the limitations of Spaciometry. We may have an n- directional structure, but in terms of intensivity that models an n- process level one! An n- process level is a terminology that also misleads in terms of the previous discussion, for there are  n-paralll processess allied with n-serial processes at each parallel, and do on!

The Potential Point therefore is very important to applying the Method beyond  spatial considerations. At the same time n-directional extensive magnitudes enable us to deal with spatial attributes in the best and most appropriate way for any and every situation involving spatial extension. However, because Hermann did not initially decompose direction into orientation and translation, it appears to us that rotation is not discussed in the system other than in a mysterious way called imaginary.

In fact rotation no longer needs to be imaginary or even as a result of an all encompassing rule of direction.  It can be introduced plainly and clearly as circular arc segments. Because of notation the " imaginary " label appears in most treatments of rotation even using line segments as a method. This is because early adopters of Hetmanns method Frnkly could not Fathom it! Gibbs wrote as much to a colleague, explaining that he did not understand Grasdmanns Multiple Algebra calculus, nor did he care for Hamiltons Quaternionic one. Neither did Paili.Clifford probably was best placed to expound upon it but he died young. Consequently the imaginary labs remain confusingly, where a simple arc segment would suffice. The superscript notation this invokes hides the simple extension atound the circle.

But we have seen this intimated by Hermann in the Vorrede.

[jehovajah]

The goal I have been striking for seems suddenly in reach.
http://www.fractalforums.com/complex-numbers/the-theory-of-stretchy-thingys/150/

Because arc segments are multi directional we cannot use direction as the all encompasding rule . Instead we could use a fixed quantity called the diameter. Normaly we use the radius nowadays and we use an arc segment called the radian ( Halbmesser ) . But the diameter is more practical when using a circular disc . The rule is that all varyings maintain the disc diameter. With that rule we create independent discs a plenty!

The varyings thus extend continuously round the disc perimeter!

 Jumping way ahead: how do these relate to products??

 Every geometrical product involves a rotation of the line segments of its perimeter. Thus the circle and the angle measures are excellent models for products, the use of exponents and logarithms thus encapsulates the process of producting and is well modelled by circular arc extensions.

Details like the quarter arc and the trig ratios are the fine tuning for this system and represent transformation relations between the various systems .

No product therefore has any meaning without rotation . Regarding multples, they borrow from this formal basis to make notatiional savings.

[jehovajah]

Let a be an extensive magnitude.

Define  a+ a+ a+ a to be a varying of  a if it is a line segment.

Define  a. a. a. a to be a varying of  a if it is a circular arc segment.

Then define 4 . a to be the varying in a line gathered together label.
Define  a⁴ ti be the varying in a circular arc gathered together  label.

But 4. a is now in the form of a circular arc variation.

If we write 4 as (4/ a). a  by the notation we can write that as  a ^{1+(4/ a)}

 That is , we can write it as a circular arc varying.

The quantity 4/ a would have to be defined as some rational variation of a circular arc extensive magnitude.

This not only looks like Hermanns quotient label, the exponent looks like Napiers proportion.

The  a is not a vector or a versor it is an extensive magnitude. The bold type is to highlight the notion of a nagnitude as opposed to a tally mark.  Thus 2 is a tally mark but  2 is an extensive magnitude.

When I see  2 I expect to see some object in space that is extensive at 2 of a unit extensive object .  When I see  1² I expect to see a unit arc magnitude extended around a circle at 2 of the unit extensive arc.

The tally count or mark 2 is totally subjective. The extensive magnitudes are objective.

So 4/ a is a ratio which can be treated like a fraction, but the outcome is a proportion of magnitude.

[jehovajah]

Commentary

The introduction of ruled varyings is crucial, both psychologically and developmentally . By imposing the simplest rules or identifying the simplest rules in behaviour we thinkingly connect to space as a magnitudinal entity that varies.

We can believe the varyings are random or whimsical and arbitrary, but ultimately we accept they have thinkable patterns, that is thought patterns, and this is where the doctrine of thought forms or rather thought patterns began its intriguing mesmerising progress to now.

The varyings are ruled by simple rules, complex rules, combined rules, whatever rules we impose or identify. One of the fundamental thought patterns is Everything Flows! Panta Rhei . Consequently we crave certainty and rigidity.

The separation between real and formal expertises accommodates these 2 contradictory states. Real expertises are empirical and ever changing, formal systems are inductive, adduced and then deducted, forming rigid patterns of thought that constantly need to play catch up to real experiences.

The trick is to keep these thought pattern rules as universal as possible. In that way they apply to most changing situations. The real defined goal for thought patterns is Invariance.

So how can a rule governing varying be Invariant!? The answer is what is really meant by being as simple as possible. A simple or one type rule has to apply across many complex situations and behaviours. Thus the simplicity is not in the rule itself but in its easy apprehension in a wide range of experiences..

The simple rule : matter is neither created or destroyed, has many additional terms and caveats and special cases and special pleadings , which it has acquired over the course of its enunciation, adoption and application. The rule is not simple. It is now quite complex.

It may be stated simply but then that is not accurate. As another example: water boils at 100°c is another rule of thumb. When the caveats are added it becomes a highly complex exponential rule!

It is these more complex formulations based on these do called simple rules that attract the name Invariant. What is usually meant is the algebraic or symbolic formulation remins unchanged in almost all circumstances.

How can that happen? By progressively reacting the formula down from its full statement to some " simplified" version of it that applies to the situation at hand. Hermanns method is all about applying these sorts of principles via the form of labelling he adopts. Because he tends to drop down from general rules he is able to see symmetries which are and would be missed by other Mathematicians and physicists and philosophers.

I have jumped ahead to the rules governing the circular arc segments, particularly because I had a defective understanding of the enticement Hermann puts in the Vorrede. Now the expositional rules come more clearly into view, and my mind races!

The notation or labelling I have sketched out in he previous post shows how these rules may be masked as definitions governing the notational devices and transformations. In particular certain manipulations, like going from in line to superscript notations make distinctions that appear in the geometrical magnitude they annotate.

The extensive magnitude in a circular arc behaves in an Analogous way to that in a straight line segment but the notation is different to emphasise as an aide memoir that the extending magnitudes, and there gatherings form different end results geometrically.

Thus  a. a is  a² an arc "length" twice as long as that of  a while  a+ a is a line segment length twice as long as that of  a. We must use r _a, the radius of the circle with the arc segment  a if we want to establish trigonometric transformations relating the 2 types of extensive magnitudes. As we do that the full complexity of these patterns begin to impress on our thought process, recogniseable and indelible patterns that enable physical dynmic behaviours to be modelled by these extending / extensive magnitudes and their established labelling rules.

[jehovajah]

I hope everyone knows by now that I am not a big fan of the number concept.,in that respect I am more extreme than. Norman
<a href="http://www.youtube.com/v/jlnBo3APRlU&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/jlnBo3APRlU&rel=1&fs=1&hd=1</a>
<a href="http://www.youtube.com/v/jlnBo3APRlU&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/jlnBo3APRlU&rel=1&fs=1&hd=1</a>

The Arithmoi and extensive magnitudes, as well as discrete entities labelled by tally marks really do not require a number concept. A structured array is fundamentally all that is needed. The Abacus is a device that illustrates this principle, but it is not the only possible accounting device used or invented in ancient times. Many sophisticated accounting devices hae been found and misunderstood by western researchers including the TaiJitu, the precursor to LaoTzus YinYang astronomical calculator , and the Antikhyterra device.

Modern computers digital and or analogue follow in a long train of accounting arrays.

[jehovajah]

One of my secret desires is to read how Napier constructed his " Artificial Numbers"  later he renamed them logarithms .

http://www.17centurymaths.com/contents/napier/constructiobookone.pdf

Babbages polynomial engine relied on extensive circular arc segments

http://youtu.be/-qx7tYWZP70
<a href="http://www.youtube.com/v/-qx7tYWZP70&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/-qx7tYWZP70&rel=1&fs=1&hd=1</a>

[jehovajah]

Watch these videos with the thought pattern " a product is the sum of simpler or primitive products".

<a href="http://www.youtube.com/v/64gIN&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/64gIN&rel=1&fs=1&hd=1</a>
<a href="http://www.youtube.com/v/64gIN_mPOrw&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/64gIN_mPOrw&rel=1&fs=1&hd=1</a>

Note also how a "parallelogram" represents a product primitive in this method.  The spatial distribution could be set out in a rectangular block , but the lattice multiplication method shows the advantage of spatially distributing it as a parallelogram.

With this method Napier did the millions of calculations he used to tabulate or Cannonise his Artificial numbers.

[jehovajah]

Here we see Napiers artificial numbers used to represent intensive magnitude, that is pitch, rather than extensive magnitude. The keys are arranged extensively because they have to be, but they are referencing the intensive magnitude rather than representing it, thus they can be equally spaced, where the intensive magnitudes themselves are not.

<a href="http://www.youtube.com/v/CekOr1pPg58&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/CekOr1pPg58&rel=1&fs=1&hd=1</a>
<a href="http://www.youtube.com/v/CekOr1pPg58&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/CekOr1pPg58&rel=1&fs=1&hd=1</a>

Our number system , the decimal and binary ones as examples share this spatiali&ntensity mix or layout. What we call a number 234 for example , is a spatial sequence of intensive valuations . We call it the place value system. Thus we distribute value in space( a geometrical device) and then ignore the spatial continuum we are using. We can instruct but we cannot ever write it down because our place value rules do not allow us to!

Extensive and intensive magnitudes do not have that issue, but rather they exhibit a different set of issues , for example tabulation is problematic.

Clearly we can use and choose whatever representations best suit our needs, and flexibly interchange between them . But. Oh no Dawg, that ain't allowed!  so we just sit and whine?

Archimedes just pragmatically solved the trisecting of an angle problem by neusis. But Oh no , that was against the rules! Then he solved it using a spiral , and perhaps several other solutions too. Yet until recently students were told it could not be solved! Now after a lot of back peddling mathematicians are more guarded in their expressions. Numbers clog up the brain with endless counting, magnitude is the brain friendly solution. I can see that is finite by constructing it. I can see 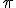is finite by drawing a circle with unit diameter. I can roll a unit diameter disc and mark off a line segment in a unique one to one correspondence with the circumference. By analogy I can use one to represent the other as extensive magnitudes in my thought patterning.

What is the problem? Certain autistic traits in mathematicians!

[jehovajah]

Change of basis in the " linear" algebra setting is the analogous process to change of base in the logarithmic or exponent setting. This represents or labes also the application of the combinatorial extensive magnitude to the algebraic intensive magnitude, as Grassmann labels things.

Why that is is due to Napier. His logarithm of Sines has been a fascination of mine because I used log and sine tables in my primary education. Ratios and fraction were always a puzzle without the historical background, and similarly sine tabulations and sine ratios were an uneasy mix. The link of course is the decimal expansion of the ratio analogised as a fraction.

Later in physics the period formula for a pendulum became a confusion. How could the formula define time when it involved time in the gravitational acceleration! Only later, much later while perusing Dimensional analysis did I find that all these measures were in fact ratios set to a quants defined as Monas, that is 1, the unit for that metric / dimensional quantity. Only now have I learned that dimension as a metric is used synonymously with extensive. I knew that the Latin means a cut away measure, but of course only extensive magnitudes can be cut into quanta. A Dimension in Dimensional analysis labels a quantum or Metron that is cut from a magnitude that can vary.

Well looking back into some 19th century geometry texts I was pleased to find the trigonometric line segments for sine , cosine  and of course the endless line for tangent. This was in the context of my Newtonian research into the unit disc and sphere, so called. De Moivre and Cotes were privy to Newtons discoveries regarding this geometry, which led to works of unequalled importance until Euler.

The trig line segment is therefore that open secret where particularly for sine an extensive magnitude is represented in the tabulations as a numerical sequence in the decimal system. The decimal sequence could be expanded to as many decimal places as represent able in some calculating device.

Thus the decimal expansion has always underpinned the labelling of a ratio of extensive magnitudes. They were always understood to be approximations or incommensurables. The move to make a "real" number " has thus always been flawed. Worse still it has obscured the richer extensive and intensive magnitude experiences that until then informed mathematicians about the space in which they have their very existence.

So Napier took a sine line segment and multiplied it by 10⁷. He was using his bones to perform the calculations, as well as the prostapharaesis method . He thus had 2 methods of checking his answer as correct to 14 decimal places. Also, by using the sine sine tables of his day, some had up to 30 or so decimal places, he had a third method of checking.

Many of his calculations were " new" results in that he was interpolating by the difference methods of his day for the appropriate reference digits( that is in minutes, seconds etc of arc.) thus what he sought to do was decrease the arc measure in whole units of equal valuation, that is by 1 unit at a time, while reducing the proportion by a binomial expansion of his base or initial sine line segment. Because what he was doing we now understand as creating from his initial sine line segment a geometrical progression of sine line segments , hissing line segments were not going to reduce by a unit, as his arc segment was constrained by him to do.

In attempting to keep these changes as uniform as possible he did nearly 10 million calculations on his own to create his cannon or table. I think, as he worked through, he realised the fabulous importance of the binomial expansion in indicating where he should be on the arc segment, and the impossibility of keeping the sine line segment difference uniform if he kept the arc segment differences uniform..

In any case he did something that Burgi did not, despite using the reducing sine line segment, he made the characteristic of a logarithm very clear for the same figures in a product that differed by powers of 10.

It s Brigg who, working with Napier just before he died , was able to show him the generality of his discovery. It did not need to be tied to the sine line segment base. In fact his distinction in the characteristic meant that the following part or the mantissa was invariant for a given string in the decimal system!  By this I mean the mantissa for 4  is the same for 40,; the mantissa for 797 is the same for 79700 etc.

The logs based on the sine line segment do not show this uniformity as well as the base 10 system, where it is optimal, but it was clear enough for Napier to make the characteristic an important aspect of his training avoiding the confusion that Burgi had within his tables( using a colour code). However it is Burgi who made clear the connection between an arithmetic and a geometric progression, which is how we understand exponential ion as reference tools today.
http://www.maa.org/publications/periodicals/convergence/logarithms-the-early-history-of-a-familiar-function-joost-b-rgi-introduces-logarithms

[jehovajah]

In group theory we have had to rethink the motion of duality , using Isomorphism and mapping to capture an analogous notion . In addition practices like commutativity and associativity have also had to BR rethought. Surprisingly it seems tha Hermann did not expect some of these familiar rules to change for extensive magnitudes.

Initially one can observe that these attributes of so called number are defined for number as a factorisation of number into number. However once extensive magnitude and intensive magnitude is introduced one really has to check if products are dual.

The Euclidean process of checking involved placing one product onto another to see if they fit! Thus orientation and translation were ignored, and both obckd are manipulated by neusis into a position wher we can judge whether they fit or not.

Then there are the transformed shapes. These have to be dealt with by a smaller Magnitude that fits into both exactly, and then the count shows duality of count or not. Associativity and commutativity  are properties of the tally marks in a count .

The disregard of extensive differences in order to keep associativity and commutativity reduces the information content of the labels. Some of that information is vital, and do we must redefine duality, associativity and commutativity for extensive magnitudes and extensive processes.

[jehovajah]

In trying to understand unabhängig, usually conveying independence, I expressed it this way.
2/3 is independent of 4/6, we can readily see it is different. But they are Analogous, so we can express one as a multiple of the other .  This means at one level dependence is captured by the notion of analogy. However specifically I could say (2/3)x is a family of such multiples where x symbolises a rational tally counter , and in that precise sense only 4/6 is dependent on 2/3. However it would be more accurate to say z4/6 is a dependant of the family (2/3)x.

Considering the plane : I could use x,y to represent 2 independent , arbitrary extensive magnitudes. Their independence is assured because they do not point in the identical direction( or for this discussion, their direct contra direction). Thus nx and my will be each a family of dependent extensive magnitudes in the precise sense explained above , where n,m are rational tally counters.

Now my point is that any combination of these 2 families of extensive magnitudes could be used to define or identify every extensive magnitude in their common plane. Each of those extensive magnitudes must necessarily be independent of each other, and the "referencing" pair or as we say the basis elements. Dependence requires that the dependants of a family of line segments precisely match the dependants of the other family of line segments.

Here is the point: to say that these families are dependent on the basis families is perverse. The families are merely referenced by the basis families, to which they are wholly independent. You may see this simply by choosing 2 different families as basis elements. The directions do not alter, merely how one references them alters.

I hope that is clear enough , and explanatory of why the idea of a 3 dimensional space is perverse. We live in an n- directional space which fortunately we can reference by at least 3 independent families of extensive magnitudes, that is by a 3 axis system where no 3 axis directions lie in the same plane. Any such axis system can form a basis for referencing all other independent axis directions. Here I use axis in the familiar sense of both extensive contra directions emanating from a point called "0" on a straight line, and maintaining that straight line orientation.

[jehovajah]

In this Grassmann framework, , that is in his construction of the familiar axes, we have to remember that work needs to be done to carefully transform what we have been taught as coordinate geometry to its presentation Grassmann style.

So I am thinking in particular of parallel families of lines. Norman does this by distinguishing a point from a vector, and then using a point and a vector to identify a particular family of vrctors( extending magnitudes) in the second step / stage system that we identify with the plane.

Here we see why Hermann exposited that intensive magnitudes , like potential points can be represented by extensive/ extending magnitudes. Norman simply changes brackets to indicate what is an intensive magnitude and what is an extensive magnitude.

(a,b) + m<x,y> where m is a rational tally marker and a,b,x,y are extensive magnitudes. a,b,x,y are thought of as fixed extensions, specified by a specific tally mark and the specified unit elements for the second stage/ rank/ grade system.however the m is thought to range through all the tally markers thus delineating the whole family of that extensive magnitude. The formula consists of a combination of 2 entities a point and a vector family, solely distinguished by the brackets and the expressed rules of thought for thre differentiated extensive magnitudes.

These kinds of formulae reference the underpinning pair of extensive magnitude families that reference every direction in the plane.

Your head may be hurting doing this kind of tautological self rereferencing but that is how it has been constructed. To make it less painful we leave out the underlying details, but we must not forget them. To slip into alternative explanatory statements , without cross referencing will lead to mixups and deviations from the construction. While these may be fortuitous and open up new viewpoints they may equally mislead and hide the freedom Hermann laboured so hard to reveal to us. It is not a freedom in space, but rather a freedom thought and construction of formal representations.