I was playing around with variants of the
arithmetic-geometric mean, and I ran into some fractals, described below. I'm not sure if they're new or not.
Given numbers w, x, ..., z, their Lehmer mean is defined as
=\frac{w^p+x^p+\cdots +z^p}{w^{p-1}+x^{p-1}+\cdots +z^{p-1}})
.
This definition only makes sense as a kind of "mean" if the arguments are positive, but let's allow complex arguments...
Given n numbers a, b, ..., d, define sequences a
k, b
k, ..., d
k by
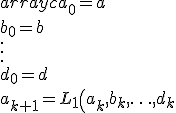 \\ b_{k+1}=L_2\left(a_k,b_k,\ldots ,d_k\right) \\ \vdots \\ d_{k+1}=L_n\left(a_k,b_k,\ldots ,d_k\right)\end{array})
When these n sequences all converge to the same limit (which always seems to happen), call this limit L*:
=\lim_{k\to \infty } \, a_k=\lim_{k\to \infty } \, b_k=\cdots =\lim_{k\to \infty } \, d_k)
.
The function L* so defined appears to be meromorphic, with fractal structure.
Consider the simple case
=L^*(1,z))
.
Here's a contour plot over the complex plane of the log of the absolute value of f
2:
Numerically, the ringed lighter-colored circles appear to be simple poles. So, this function f
2 has a single large pole at -1, with two "smaller subpoles", each of which have two "smaller subpoles" of their own, and so on, approaching a Cantor set. Not sure what happens right at the limit points. The function appears to have no zeros.
Here's a plot of
=L^*(1,1,z))
, with a zoomed-in view on the right:
Here are f
4, f
5, and a zoom of f
5:
Here's one where the fixed arguments are asymmetrically arranged:
Some analysis:
The Lehmer means are rational (quotient of two polynomials) functions of their arguments. Therefore any finite composition of them will also be a rational function. The poles appear wherever a denominator becomes zero at some iteration. (Very large values cause Lehmer means to become very large.)
In the f
2(z) = L*(1,z) case above, the degree of the denominators approximately doubles at every iteration, so twice as many poles are added at each step. For this reason, the bifurcating fractal structure of the poles is maybe not surprising.
The poles appear at algebraic points because the denominators are polynomials and the fixed argument (1) is algebraic. Here the locations of the first few poles of f
2 are labeled:
Here's an oblique view of |f
2(z)|:
I've looked numerically at the power series for f
2, but haven't been able to recognize the coefficients. The coefficients are rational if you expand at z = 1. The numerical residues of the poles appear to be algebraic multiples of f
2(0). I've also numerically looked for a differential equation that f
2 satisfies, but haven't found anything simple...
October 06, 2006, 06:14:46 PM
Dilber MC Theme by HarzeM