compiling Kalles Fraktaler with mingw

[gerrit]

Try again posting example image...
http://www.fractalforums.com/index.php?action=gallery;sa=view;id=20577

[claude]

One more result: using the average of normal and diagonal central differences does improve a bit over just central. See example.
So the squared length of the gradient of map m at point x,y is taken to be the mean:

(de-quoting so the formulas appear)

with




(end of quote)

Thanks for the formulas, its very clear.

I (hopefully) fixed your image link, you need the bbcode variant under the image on the gallery page: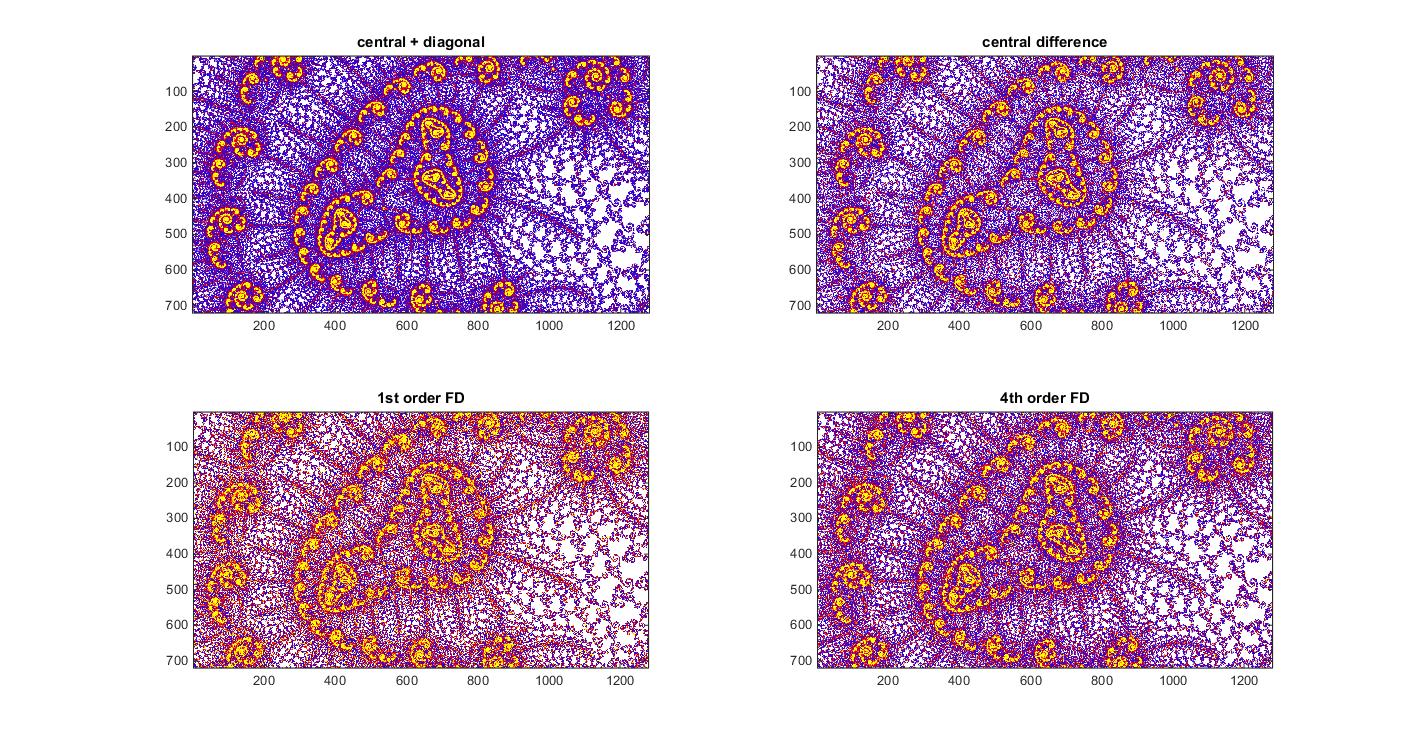


Top left sub-image does look a lot better, but it changes the overall tint of the image a lot too with that palette, so maybe I make the central differences a checkbox in the colouring dialog, the default would have to be disabled for backward compatibility.

[gerrit]

Top left sub-image does look a lot better, but it changes the overall tint of the image a lot too with that palette, so maybe I make the central differences a checkbox in the colouring dialog, the default would have to be disabled for backward compatibility.

I wouldn't take these images too seriously except to demonstrate gradient computation. MATLAB does some scaling, so if one image has a different maximum even on one pixel it will scale the color map giving a different overall tint.

FYI I loaded the .kfb file, extracted the "counts". Then pass counts through a transfer function with p for example 0.5 or 2 (whatever looks cool). Then compute , then pass z through another transfer function (or a power, whatever looks nice). This is probably not exactly what KF does, I stole the ideas from your  pseudo-de.c code (thanks!).

[claude]

Ok. I implemented it (with no transfer function before differencing, and using log(1+||g||) instead of the log(1/sqrt(1+||g||^2)) stuff, which I think mostly just adds a scaling factor).
For the averaging of the directions I tried l2 norm (like your equations) and l1 norm (sum of abs, as used by KF for the original forward difference method), they seem visually very similar https://en.wikipedia.org/wiki/Norm_(mathematics)#p-norm

Personally I don't like the results though.  Ignoring the overall colour shift in the attached (seems tweaking the IterDiv setting to match one part doesn't fix all parts...), there are several points of note:

1. the 2x2 forward difference has a smoother transition from flat to boundary
2. thin axis-aligned features have a "flat" interior with linear halo on either side (see lower right hand side)
3. isolated high points have a square halo around them (visible in the yellow on orange in the middle of the lower half)
4. the 3x3 central difference higher iteration parts looks fatter and blockier (the other has finer details)

Point 2 above is the real deal-breaker for me.  But having already written the code, I may as well keep it in case someone else prefers it, so it'll probably be in the next release anyway.  Meanwhile I'm rendering a higher resolution version of the attached, to see how it looks with AA, maybe I'll be won over.

EDIT here's a version with 4x4 supersampling for antialiasing - I think both methods look about equal, though I slightly prefer the bottom (central derivative) version: https://mathr.co.uk/mandelbrot/2017-09-22_forward-vs-central-differences-4x4aa.png 3.7MB

[gerrit]

I agree this simple solution does not seem to deliver, it looks better at a few spots, but much worse in others. Fractal functions perhaps do not obey the usual rules of numerical methods.

I'm guessing the unwanted "holes" arise when we have, say, m(x-1)=10, m(x)=1000, m(x+1) = 10. In that case the central difference will give zero, but the 1st order forward difference will be more "correct".  Perhaps some method could be devised to switch when required.

It reminds me of the switching method used in regularization, which also boils down to somehow defining the norm of the gradient of a function which is non-smooth at certain places.

For example slide 41 in
http://www.unige.ch/math/hairer60/pres/ASCHER%20bbtime.pdf

Great that you actually implemented this, maybe it can be made to work somehow. It is a bit of a problem that you have to oversample by such large amounts to get it to look nice, esp. when making movies.

[gerrit]

EDIT here's a version with 4x4 supersampling for antialiasing - I think both methods look about equal, though I slightly prefer the bottom (central derivative) version: https://mathr.co.uk/mandelbrot/2017-09-22_forward-vs-central-differences-4x4aa.png 3.7MB

Thanks for the amendmend. I guess it shows not to draw conclusions from a single data point. I've mainly tried 2X2 oversampling, as that is required for any coloring method. It would be great if it could work for DE too.

Did you include the diagonal central differences? That seems right as it uses all 8 neighbours of the pixel under consideration but, perhaps problematically, not the actual pixel.

Looking forward to the new build. (And perhaps windows compile manual? Cygwin based perhaps? (If you give a finger he takes the whole hand, as the Dutch say.))

[claude]

Compiling on Windows is not my expertise, sorry - I have no Windows machines to try with - I cross compile from Debian.  Maybe I should try a Windows virtual machine, I heard Microsoft makes available free (as in beer) versions for testing purposes?  Or maybe you could try a Debian virtual machine, the build instructions for that OS are up to date.

I included the diagonals in the central differencing.  This is the current code, where double p[3][3] contains the neighbourhood of the pixel:

Code:

switch (m_nDifferences)
{
case Differences_Central3x3:
	{
		// gerrit's central difference formula
		double gx = (p[2][1] - p[0][1]) * 0.5;
		double gy = (p[1][2] - p[1][0]) * 0.5;
		double g1 = (p[2][2] - p[0][0]) * 0.35355339059327373; // 1/(2 sqrt(2))
		double g2 = (p[2][0] - p[2][0]) * 0.35355339059327373;
		double g = sqrt(0.5 * (gx*gx + gy*gy + g1*g1 + g2*g2));
		iter = g * 2.8284271247461903;
	}
	break;
case Differences_Forward3x3:
	{
		// forward differencing in 8 directions from the target point
		double gx0 = (p[0][1] - p[1][1]);
		double gx2 = (p[2][1] - p[1][1]);
		double gy0 = (p[1][0] - p[1][1]);
		double gy2 = (p[1][2] - p[1][1]);
		double gu0 = (p[0][0] - p[1][1]) * 0.7071067811865475; // 1/sqrt(2)
		double gu2 = (p[2][2] - p[1][1]) * 0.7071067811865475;
		double gv0 = (p[2][0] - p[1][1]) * 0.7071067811865475;
		double gv2 = (p[0][2] - p[1][1]) * 0.7071067811865475;
		double g = sqrt(0.25 * (gx0*gx0 + gx2*gx2 + gy0*gy0 + gy2*gy2 + gu0*gu0 + gu2*gu2 + gv0*gv0 + gv2*gv2));
		iter = g * 2.8284271247461903;
	}
	break;
case Differences_Diagonal2x2:
	{
		// forward differencing in 2 diagonals of a 2x2 substencil
		double gu = (p[0][0] - p[1][1]) * 0.7071067811865475; // 1/sqrt(2)
		double gv = (p[0][1] - p[1][0]) * 0.7071067811865475;
		double g = sqrt(gu * gu + gv * gv);
		iter = g * 2.8284271247461903;
	}
	break;
case Differences_Traditional:
	{
		// traditional method reverse engineered from original code
		double gx = (p[0][1] - p[1][1]) * 1.414;
		double gy = (p[1][0] - p[1][1]) * 1.414;
		double gu = (p[0][0] - p[1][1]);
		double gv = (p[0][2] - p[1][1]);
		double g = fabs(gx) + fabs(gy) + fabs(gu) + fabs(gv);
		iter = g;
	}
	break;
}

A comparison is attached, without any supersampling/AA.  Clockwise from top left: Traditional, Forward 3x3, Central 3x3, Diagonal 2x2

[gerrit]

I tried in MATLAB and seems the choice is between Forward3X3 and Central3X3.
Below two image examples. To me Central3X3 looks better in the first, but Forward3X3 looks better in the second.

[gerrit]

I ran some more tests comparing Central 3X3 with Forward 3X3. I rendered DE

at 1920X1080 with AA up to 9X9 (KF 2.12.2 crashed when trying to render at

19200X10800). Results are here:

http://persianney.com/fractal/de/

[claude]

(KF 2.12.2 crashed when trying to render at 19200X10800).

The theoretical maximum image size for the 64bit version at 16x9 aspect ratio is 35664x20061, this hard limit is 2 GiB of bitmap data.  The 32bit version will be limited further to 4GiB memory per process, by the size of the iteration array (8 bytes per pixel, bitmap is 3 bytes per pixel, plus at least 16 bytes per reference iteration).  On my desktop (with 8GiB ram and 8GiB swap (page file)) I had no problems with a 19200x10800 test render, other than some slowness due to swapping / paging.

But there is no error checking, so if bitmap creation fails (for example due to out of memory) KF crashes
I added this to the bugs list so I remember to fix it.

[gerrit]

The theoretical maximum image size for the 64bit version at 16x9 aspect ratio is 35664x20061, this hard limit is 2 GiB of bitmap data.  The 32bit version will be limited further to 4GiB memory per process, by the size of the iteration array (8 bytes per pixel, bitmap is 3 bytes per pixel, plus at least 16 bytes per reference iteration).  On my desktop (with 8GiB ram and 8GiB swap (page file)) I had no problems with a 19200x10800 test render, other than some slowness due to swapping / paging.

But there is no error checking, so if bitmap creation fails (for example due to out of memory) KF crashes
I added this to the bugs list so I remember to fix it.

FYI it crashes after finishing the first reference orbit (even at zoom=1). 64 bit, 32G of RAM, MSWin7/10. Kalle's binary does not crash.

BTW it (all versions) hangs if you accidentally zoom in on the period 1 bulb. 

[gerrit]

FYI it crashes after finishing the first reference orbit (even at zoom=1). 64 bit, 32G of RAM, MSWin7/10. Kalle's binary does not crash.

Correction: Kalle's binary goes into infinite loop at Ref:2 hogging 1 cpu,which is not an improvement. I tried on 2 different Windows machines.

[claude]

FYI it crashes after finishing the first reference orbit (even at zoom=1). 64 bit, 32G of RAM, MSWin7/10.

That sounds like it crashes on the first attempt to access image data, whether iteration arrays or bmp colours is hard to say without more information.  This is consistent with memory allocation failures not being handled properly, the crash is probably dereferencing a null pointer.

BTW it (all versions) hangs if you accidentally zoom in on the period 1 bulb. 

I can't reproduce this.

[claude]

New version 2.12.3 available at the usual https://mathr.co.uk/kf/kf.html :

- multiple differencing methods for distance colouring (thanks to gerrit)
- bugfixes to examine zoom sequence (thanks to Dinkydau and Fractal universe for reporting)
- raised reference count limit from 199 to 10000, default remains 69
- settable additional reference count in examine zoom sequence, default remains 10

[Kalles Fraktaler]

Excellent!