Implemented the Mandelbrot loop in Lisp.

[Pauldelbrot]

The really interesting thing is, it's a macro, and it can be called simply with "(:= z (+ (** z 2) c))" and it will spit out a loop that calculates the M-set.

Not only that, it takes two parameters, bitsprecision and a number-system object. If bitsprecision is high enough, it will spit out a loop that uses bignums instead of IEEE doubles. Orthogonally, the number-system object is defined in terms of a list of unit-symbols, a unit multiplication table, and a collection of functions for reciprocal and transcendental functions. Passing different number systems to the macro generates different versions of the loop. I could generate a loop that iterated only real numbers (say, for generating a bifurcation diagram), and I've also implemented the number system objects for quaternions and what Fractint calls hypercomplex numbers (except no transcendentals yet; I have to implement those for bignum reals and for non-reals.)

Basically, it does symbolic algebra to convert the input assignment-like expressions and number-system info into more assignment-like expressions, representing the same math but decomposed into the individual real-number components. So two input-expressions become four with complex arithmetic and eight with quaternions. These are then subjected to algebraic simplification, which can extract common factors, apply the distributive rule, collect like terms, and similarly -- this step turns a (+ (* z-r z-i) (* z-i z-r)) into a (* 2 z-r z-i) in the case of the standard Mandelbrot fractal, for example. Yes, it does detect if terms are the same even if products or sums are rearranged. And since this step is applied after reduction to real-number arithmetic, it doesn't matter that quaternions are noncommutative; by the time simplify sees quat expressions, they're groups of four real expressions rather than quat expressions, and real multiplication is commutative.

The upshot: by implementing a fair bit of a symbolic-algebra package and one lousy macro I have ANY non-transcendental map, to ANY precision, in real, complex, quaternion, or hypercomplex arithmetic.

I don't have to write the inner loops for everything separately. The computer does it for me.

Best of all, the loops are fast. The IEEE double loop it spits out for plain old complex quadratic Mandelbrot is 40% faster than Ultra Fractal's inner loop. The bignum loop is 7 times slower than UF's at 22 decimals, for now, but I plan to fix that. Plus this thing will get speed enhancements elsewhere.

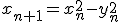
For starters, the system can in fact compile a loop on the fly for each specific image, or even each layer, with parameter values baked in as constants. So if I want to generate a Julia set image for c = i, the loop it generates will be short one add because the real part of c is zero and it can just generate a loop that has . (Ultra Fractal can do this too, but only in the context of its formula interpreter. My macro does it and puts out native code.)

Furthermore, some stuff you can't do in UF without multiple layers that duplicate one another's calculations, this software will do with a single calculation of each pixel and smarter handling of the resulting data. I also plan to have faster bailout tests: instead of looking for convergence to a possibly-expensive-to-test shape, it will run a high speed loop that tests for exit of a square or circular area, then iterate a lower-speed loop until it hits the target shape. So for most iterations, say 999700+ out of 1 million for a deep point, it will not be using the expensive bailout test.

The Lisp being used is Clojure, which runs on a JVM. This means this stuff is portable to every system that has a JVM, fast on every system that has a good JITting JVM, and interoperates nicely with Java. (The current bignum implementation, which sucks, uses java.math.BigDecimal. I will probably adapt the BSD-licensed JScience LargeInteger code to make a custom one that's faster, particularly by using Karatsuba multiplication when it gets really REALLY big. With that, it will probably beat Fractint(!) at hundreds of decimals.)

The Java interoperation means programs built on this core have ready access to GUI, PNG encode/decode, other image formats, the network, and so forth.

Last but not least, Clojure's eval is available at deployment time, so the formula parser is nearly fully written: the user will be able to just type "z^4 - z^2 + c" and the computer will grind away, compile a function to JVM byte-codes to iterate that really really fast, and off it goes, with the JIT putting the finishing touch on it.

Did I mention that the loop-generating code does common subexpression elimination? And that all of this has been tested and found to work? 100 million iterations in under 700msec on my E5200; UF takes about 1 second to do that many iterations on one core on the standard Mandelbrot zoomed into the cardioid and with guessing and periodicity checking turned off.

That, by the way, is what's next: adding periodicity logic to the emitted loops, controlled by a parameter, and a slightly smarter bailout. Right now it generates a circular/spherical bailout zone, though it also does common subexpression elimination between the iteration steps and computing the squared modulus. It needs to be smarter: detecting if it's cheaper to test a sphere or a square and choosing accordingly what code to emit. For the normal M-set, a sphere is cheap because x² and y² are needed anyway. Add an add and a compare and you've got your bailout test, versus four compares for a square bailout. On the other hand, if there were no x² or y² already needed elsewhere, the circular bailout test becomes two multiplies, an add, and a compare instead of four compares. Since adds, subtracts, and compares tend to be comparable in expense and multiplies tend to be more expensive than any of those, four compares is cheaper in this instance. A multiply, an add, and a compare might be cheaper than four compares though, so it might be worthwhile to use a sphere if it's a complex number and one of the squares is needed. For higher dimensions d, there are 2d compares needed for a hypercube, d multiplies, d minus one adds, and a compare needed for a sphere, so many of the squares would need to be already needed for this to be a winner. How many? Probably hardware-dependent. I'll have to experiment.

Further down the line: add distance estimator capability. I've determined that to support most of the common colorings, and many of my own custom ones, you just need the last iterate and the number of iterations. The major exceptions:

• Distance estimator, Lyapunov exponent, and similar require the derivative. Add another boolean flag to the parameter list and a bit more symbolic algebra and we can emit loops that compute the derivative.
• Assorted things, like traps, that use the whole orbit.

Clojure supports a concept of lazy sequences, so we can generate a lazy sequence of iterates that, under the hood, runs a fast iteration loop to spit out 64,000 at a time (or however many), then trickles these out to the sequence's consumer, then generates some more. Alternatively, the caller can just feed the existing macro a few extra expressions to compute to accumulate a weighted sum or whatever.

Heck, I don't even need to add a flag to compute a derivative/Jacobian; I can just create symbolic algebra code to compute how to compute the derivative/Jacobian and then append those to the list of expressions fed to the macro. The output loop will compute them all and the derivative will be right after the last iterate in the array of output values. And the macro will do common subexpression elimination between all of these various calculations, so if xy appears in a lot of places, the output code will assign it to a temporary and then use that repeatedly.

Oh, and did I mention I've implemented what I've implemented so far in four days? In a week at that rate I'll have derivatives, Jacobians, and what-have-you. (Yes, it already will iterate functions of more than one variable, such as the Henon map.) In a month at that rate, a working demo that renders PNG images and breaks all kinds of speed records.

It's shocking that nobody much else is apparently developing fractal software in Lisp, given what it's capable of.

[Pauldelbrot]

For higher dimensions d, there are 2d compares needed for a hypercube, d multiplies, d minus one adds, and a compare needed for a sphere, so many of the squares would need to be already needed for this to be a winner. How many? Probably hardware-dependent. I'll have to experiment.

To hell with experimenting. I'll just have the computer do it. It would be easy to add a flag parameter to generate either spherical or cubical bailout zones and then a wrapper function to generate both, test them on an interior point, and return the faster one.

Finding an interior point might be difficult. Sometimes there are none -- disconnected quadratic Julia sets come to mind. Maybe for the speed tests it can generate loops that do the bailout test but don't actually quit if it's triggered, run each a few times so the JIT kicks in, then generate a normal bailing-out loop using whichever method was faster. Of course, stopping the compiler optimizer eliminating the unused test would be tricky. Perhaps use the test to flip the sign of a number, so it matters semantically, in dummy loops. In those dummy loops the actual iterations don't matter anyway, other than how fast or slow they are.

[Pauldelbrot]

To hell with experimenting. I'll just have the computer do it. It would be easy to add a flag parameter to generate either spherical or cubical bailout zones and then a wrapper function to generate both, test them on an interior point, and return the faster one.

Finding an interior point might be difficult. Sometimes there are none -- disconnected quadratic Julia sets come to mind. Maybe for the speed tests it can generate loops that do the bailout test but don't actually quit if it's triggered, run each a few times so the JIT kicks in, then generate a normal bailing-out loop using whichever method was faster. Of course, stopping the compiler optimizer eliminating the unused test would be tricky. Perhaps use the test to flip the sign of a number, so it matters semantically, in dummy loops. In those dummy loops the actual iterations don't matter anyway, other than how fast or slow they are.

Done. In fact, the original macro is now a function that returns a function (so, a higher-order function, albeit one that actually compiles its return value ). It now takes several new or changed parameters. The bailout may now be positive, negative, zero, or nil. Nil means no bailout test, for mappings with no attractor at infinity. Zero means only use a passed-in bailout function. Positive means spherical bailout with that radius. Negative means cubical bailout with doubled absolute value as side length. The emitted function will, if the bailout wasn't zero, run a high speed loop until the bailout or the iteration limit is hit. Then, if the caller supplied a symbol instead of nil for the bailout test function, it will loop some more this time calling the function bound to the supplied symbol for the bailout test.

So if for instance we want a star-shaped bailout area in which a circle of radius 5 centered on the origin can be inscribed without clipping the inner points and in which a square of side length 4 centered on the origin can be inscribed without clipping the inner points, we can call the function with a bailout number of 5 or -4 and the syntax-quoted name of a test function that takes two arguments (for the complex case) and decides if it's outside the star yet, and get back a loop that will run until the point lands outside the circle or square using the fast test for such a shape, and then iterates a bit more until the star-test function returns true to indicate the point landed outside the star. The function returns with the first iterate that landed outside the star, but a lot faster than if it did a complicated test for a star-shaped region every iteration.

In addition, it does loop unrolling, controlled by another parameter. 1 yields normal loops. 2 or higher unrolls the loop and moves the iteration counting outside of the unrolled portion; so instead of

Code:

maxit = 1000
i = 0
z = 0
c = pixel
loop {
  if i > maxit return :iters, i, z
  if |z| > 2 return :infty, i, z
  z = z^2 + c
  i = i + 1
}

it might be

Code:

maxit = 500
i = 0
z = 0
c = pixel
loop {
  if i > maxit return :iters, i * 2, z
  if |z| > 2 return :infty, i, z
  z = z^2 + c
  if |z| > 2 return :infty, i + 1, z
  z = z^2 + c
  i = i + 1
}

or even

Code:

maxit = 250
i = 0
z = 0
c = pixel
loop {
  if i > maxit return :iters, i * 4, z
  if |z| > 2 return :infty, i, z
  z = z^2 + c
  if |z| > 2 return :infty, i + 1, z
  z = z^2 + c
  if |z| > 2 return :infty, i + 2, z
  z = z^2 + c
  if |z| > 2 return :infty, i + 3, z
  z = z^2 + c
  i = i + 1
}

and in theory this could save time by only testing and incrementing i every nth iteration.

Last but not least there's a driver function that takes some of the parameters, including separate circular and square bailouts, and calls the function-generator with various combinations of square or circular bailout and unrolling amount, passing a flag that generates a dummy function that just takes maxiters, treats the other input parameters as zeros, and doesn't really bail out though it does the bailout tests. These are all timed, and whichever combination of parameters yields the fastest time is used to produce a non-dummy iteration function that is then returned. The timing function runs the dummy iterator through a million iterations fifteen times in a row, averaging the time taken for the last ten runs; the first five are discarded, since the JIT won't have kicked in for the first few.

So far, it almost always chooses the circular bailout and a non-unrolled loop; almost every nontrivial nonlinear function of z involves x² and y². Interestingly, it prefers circular bailout even to iterate z = z + c, which doesn't involve x² or y². Perhaps the E5200 I'm running it on has a very fast fmul instruction?

Regardless, I've continued testing the stock M-set iteration, and it continues to emit a loop for it that completes in a blistering 7 nanoseconds on this box. That's maybe 17 CPU cycles. I can account for most of them:

Code:

branch if i > max
x2 = x^2
y2 = y^2
branch if (x2 + y2) > b
y = 2*x*y + a
x = x2 - y2 + c
inc i
loop

Integer compare, branch, fmul, fmul, fadd, float compare, branch, fmul, fmul, fadd, fsub, fadd, inc, branch; that's at least fourteen cycles right there. A couple of the instructions are probably not able to be pipelined, accounting for the other three. The code I wrote, combined with Clojure's compiler and Sun's Hotspot server VM JIT, appears to be generating about the fastest loop possible.

Did I mention I've added distance estimator? Well, not quite. But the iterator-generator can take some forms representing the mapping and now also another collection of forms representing auxiliary computations, which will be performed each time around the loop but whose loop variables won't participate in bailout calculations. The auxiliary computations can, and generally will, refer to the variables in the mapping (e.g. z). Perfect for accumulating the derivative for distance estimator, or similarly.

Next up: adding another flag to emit a loop either with or without periodicity checking, perhaps even a specific period to look for.

[cKleinhuis]

wonderful, i love such detailed monolugizes

cheers

[Pauldelbrot]

wonderful, i love such detailed monolugizes

cheers

Thanks.

Loop-generator can now emit iteration functions like before, or with extra parameters and with a spherical or a square test for the iterated point hitting a point specified by the extra parameters.

This will be used for:

• Periodicity checking: Brent's algorithm can be implemented by calling the function repeatedly, with exponentially rising iteration limits, until a master iteration limit is hit, bailout occurs, or periodicity is detected, each time calling the function with the initial point equal to the final iterate of the previous batch of iterations and the point to test for being that same point.
• Checking for a specific period: Similar to above, but each sub-loop uses the same iteration limit, the period to check for or a multiple of it.
• Checking for a known finite attractor: Just put the attractor point in the extra parameters.

It may seem limited, that it will only check for one point, but this is actually a feature, not a bug. In practise, when any rendering method hits a point that goes to a particular attractor, it tends to hit lots more in a row that share the same fate, simply because basins, M-set components, and the like tend to be unions of contiguous regions of space. So, the iterator will do something like this:

• If last point escaped, iterate current point with a loop with no periodicity check. It will escape or hit iter limit.
• If last point hit iter limit, and it landed on an image-global attractor (e.g. 0 in an Antimatter M-set calc or the finite attractor in a quadratic Julia set calc), iterate current point with a check for that attractor.
• If last point hit iter limit, and it did not land on an image-global attractor, determine period of last point if any. If aperiodic, iterate current point with Brent's algorithm, then discover period. Otherwise, iterate current point checking for known period.
• If last point hit an image-global attractor, iterate current point with a check for that attractor.
• If last point didn't hit an image-global attractor but ended up periodic, iterate current point checking for that period.

For the quadratic M-set iteration, the no-check loop emitted runs at 7ns per iteration; the checking loop runs at about 10ns per iteration. The no-check loop, being 30% faster, is therefore preferred if it's likely the current point will escape.

The checking loop is clearly preferred otherwise, with some check or another: my test point 0.2 + 0.1i (near the set's cardioid cusp) lands on 0.21556775949710844 + 0.1757887921270715i. With an iteration limit of 100,000,000, the no-check loop takes 700ms to discover this fact, whereas the checking loop with that attractor plugged in iterates 25 times and stops, taking 150 microseconds, at 0.21556774298091957 + 0.17578884455030708i.

25 iterations of the checking loop takes 250ns, so nearly all of those 150 microseconds are function-call overhead! This indicates that the minimum number of sub-loop iterations when chaining should be 150 microseconds worth, or 15,000 iterations(!) in the case of the normal M-set loop. I will add a function to the code to compute this minimum for whatever actual mapping is being used; this should be simple: 150,000 divided by average-time-to-execute-one-iteration-in-nanoseconds.

[Nahee_Enterprises]

It's shocking that nobody much else is apparently developing
fractal software in Lisp, given what it's capable of.  

I can see that you are really on a roll with this, and very much stoked.  I would cheer you on, but I am afraid what it would do to you in your current state of arousal.        

Keep us informed as to the current progress.  I am curious about comparison times once you have completed the bulk of the coding.  (And would love trying it out.)   

[David Makin]

It's shocking that nobody much else is apparently developing fractal software in Lisp, given what it's capable of.

When your project is in a form others can use then please count me in as a beta tester
Also - what development software are you using ?

[Pauldelbrot]

When your project is in a form others can use then please count me in as a beta tester
Also - what development software are you using ?

NetBeans.

[Pauldelbrot]

Periodicity checking added more fully to loop generator. I found that the Clojure function call overhead was fairly steep, to the point that one function call took as long as 15,000 raw Mandelbrot iterations, so I rewrote the loop generator to take two more parameters, per-check? and per-check-brent?, and if either was present, wrap its output loop in an outer loop that implements the appropriate algorithm.

It can now output four kinds of loop:

• A loop optimized for points predicted to escape; no check for finite attractors or periodicity.
  
  
• A loop optimized for points predicted to go to a particular finite attractor; it checks every iteration for approach to the attractor. The overhead of doing so is about 33%, or 1/3 of an iteration, so doing this every iteration isn't horrid.
  
  
• A loop optimized for points predicted to go to an attractor of a particular period. This one saves the point, iterates N times, compares, iterates N times, compares, and so on, with N a multiple of the period. The inner iteration loop is as fast as the escaper loop.
  
  The outer loop overhead for periodicity checking is over 64 iterations because of the time involved in passing the results of the inner loop to the outer loop in a list and extracting them again there. (Oddly, passing them in a vector is slower, and passing them in with-local-vars is much slower.) Therefore I have set it to use as a step size the next multiple of the passed-in period higher than a passed-in minimum value.
  
  
• A loop that uses a modified Brent's Algorithm for cycle detection, with the powers of two replaced by integers close to successive powers of an arbitrary real number, and with the values lower than a passed-in minimum chopped off the head of the sequence. The Brent inner loop is the same speed as the finite-attractor-checking loop, and in fact is the same code. It checks every iteration for approach to a saved point. The outer loop runs the inner loop until the total iterations hits a power, saves the point, runs it some more, etc.
  
  Since these points become exponentially farther separated, the Brent outer loop overhead is logarithmic in max-iters instead of linear, making it less important to performance-tune the outer-loop code. As a result I use Clojure sequence abstractions to generate the power sequence.

The inner loops are limited to 32-bit integer iteration counts, so if for instance the step size in the specific-period-check is bigger than about 2 billion, the largest factor of the period smaller than that will be used instead, and the Brent algorithm will switch eventually from powers to a linear sequence. The first two loop types actually come out with a period-check loop checking for a very large (around 2 billion) period.

The outer loops can use bignums to count iterations, though on present-day hardware, only ones in the low billions will be very useful.

All this has, as usual, already been tested and seen to work. Including running a Mandelbrot point through five billion iterations, more than a 32-bit integer can track, at decent speed because bignum arithmetic is only used every couple of billion iterations. (It stopped at about the size limit of a 32-bit unsigned integer, actually, but not because of any bug; rather, because that iteration was the same as iteration 2147483647, and the way it handles bigger max-iters values is to force on period-testing with that period.

And last but not least, this was generated from a generated loop:

Code:

.........................................
.........................................
.........................................
.........................................
.........................................
....................#....................
..................##.....................
...............#.#####...................
..............##########.................
.........###.###########.................
#######################..................
.........###.###########.................
..............##########.................
...............#.#####...................
..................##.....................
....................#....................
.........................................
.........................................
.........................................
.........................................
.........................................

[Pauldelbrot]

Code:

.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
........................................#........................................
.................................................................................
....................................####.........................................
....................................####.........................................
..............................#..##########......................................
..............................#################..................................
............................###################..................................
...........................#####################.................................
.................#######..######################.................................
................#########.######################.................................
##############################################...................................
................#########.######################.................................
.................#######..######################.................................
...........................#####################.................................
............................###################..................................
..............................#################..................................
..............................#..##########......................................
....................................####.........................................
....................................####.........................................
.................................................................................
........................................#........................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................
.................................................................................

What's missing from this picture is the impressive accuracy. Iteration limit: five billion, with a "b".

It took three seconds to spit that out, thanks to Brent's algorithm.

[cKleinhuis]

oh, with that iteration depth it would be interesting to make a new "DEEPEST MANDELBROT" picture
 

[Pauldelbrot]

Didn't do as much today, as I was busy much of the day with other things.

But it now has code to measure the costs of the basic arithmetic operations, add, subtract, negate, multiply, and divide, on whatever type of number is being used. So far, the formula compiler only uses this to optimize some expressions of the form (* 2 x y) into (+ (* x y) (* x y)) and the like (which, with common subexpression elimination, will end up an add and a multiply instead of two multiplies). Any multiplication with an integer coefficient is potentially replaceable with a sum, a negation, or a negation of a sum. The question is whether a multiply costs more than n minus one adds and possibly a negation. The costs of adds, multiplies, and negations are benchmarked for each newly-seen precision of bignum, and for doubles, and when the compiler is called upon to supply a loop for a particular mapping at a particular precision, it will use this data to optimize the loop.

On my hardware, all the basic FP operations take the same amount of time, so the normal Mandelbrot inner loop's y recurrence is (* 2 (* x y)) after being broken down into unary and binary expressions. But for bignum arithmetic, a multiply is almost always costlier than an add so this becomes (+ (* x y) (* x y)) with CSE reducing that to one multiply and one add.

It changes * 2 and * 3 to sums immediately when bignums first are needed, but * 37 is not changed into an add before the number of bits of precision gets into the upper hundreds.

The next planned optimization is to generate all the possible breakdowns into binary operations, including extracting common factors from sums, and tot up the costs of each version, picking the version that is cheapest.

[Pauldelbrot]

Not gotten much done. I did build the expression rearranger, but testing it revealed a problem. I knew the number of possible rearrangements would grow exponentially, but it turns out to be a very FAST exponential. The real component of z² + c has six possible variations; that of z³ + c 29, that of z⁴ + c over 700, and that of z⁵ + c enough to crash the computer.

Needless to say, another approach to optimizing is needed. There are three major optimization possibilities:

• Turning multiplies by small integers into adds (BigDecimal)* or shifts-and-adds (custom bignums). I've since realized that then number of adds can be improved from linear in the integer to logarithmic -- not ((x + x) + x) + x ... but ((x + x) + (x + x)) + ((x + x) + (x + x)) + ... (with common subexpression elimination). Dependent on bignum size.
• Extracting common factors from sums, to get rid of more multiplies. Always an improvement, if it weren't for:
• Common subexpression elimination. The thing is that arranging the terms differently can result in different outcomes. For example, the real part of z³  is (+ (* x x x) (* -3 y y x)) (now using Lisp's prefix notation) and the imaginary part is (+ (* -1 y y y) (* 3 x y x)). (That's how it actually gets output by the conversion to real numbers followed by simplification. You don't want to know what it looks like before simplification.) The current expression grouper turns those multiplies into a simple left-to-right sequence, like (* (* (* -3 y) y) x) (and turns (* -1 foo) into (- foo)). The way it is grouped affects CSE, in this case denying an opportunity to optimize the repeated need for y².

The trickiness is that CSE interacts unfavorably with common factors -- if we have (+ (* 2 x y) (* 2 x z)) we can extract out a common factor of (* 2 x) and turn four multiplies into three. On the other hand, if elsewhere we have (+ (* 2 y) (* 2 z)) CSE can factor out the latter products, saving two multiplies, if the sums don't get simplified; if they do, it can factor out (+ x y). CSE now saves an add, but no multiplies. On the other hand, factoring saved two multiplies in this case, one from each sum. If the expression grouper chooses to group the first factored sum as (* x (* 2 (+ y z))) CSE can factor out the inner product, saving another multiply, but not if the expression grouper groups the product with x in the inner product. So this example shows that the expression grouper needs to be smarter about CSE opportunities somehow.

Another case would be a three-term sum with two terms sharing a common factor, and a different two terms a different one. How should (+ (* 2 x) (* 2 y z) (* z x)) be factored? As (+ (* 2 (+ x (* y z))) (* z x)), as (+ (* 2 x) (* z (+ (* 2 y) x))), or as (+ (* x (+ 2 z)) (* 2 y z))? All three save a multiply, so any difference between them will come from how they interact with CSE; if there are lots of occurrences of 2z as a factor in various products, the third one is the winner, whereas if there are lots of occurrences of yz elsewhere in the expressions to be calculated, the first one is the winner, while lots of xy would make number two come out on top.

One thought I had was to find every possible subexpression and see which ones occurred the most, eliminating those first and rearranging to suit, but that runs afoul of exponential growth again, and my experimental code for it also seems to unfortunately provoke an implementation bug of some sort, which I still have not heard back from the tool-chain developers about.

Now I'm thinking I may have to resort to a few heuristics, such as to prefer to keep squares and higher powers together (they can benefit from internal CSE and CSE with circular-bailout calculations) and to build a list of the subexpressions as it groups terms, rather than later, and have the already-listed subexpressions influence future term-grouping (to favor keeping copies of such subexpressions together, enabling CSE). This can be done in one optimization pass, with small-integer products optimized into adds, or shifts-and-adds, in a second pass afterward.

* It occurs to me that it might be more efficient to bit-shift a BigDecimal than add it to itself, perhaps recursively; though BigDecimal has no shift methods,  (BigDecimal. (.shiftLeft (.unscaledValue x) n) (.scale x)) will multiply x by 2ⁿ and may be faster, at least for larger n. (Tested, works; with x = 17 and n = 2, produced 68, as expected.)

[Pauldelbrot]

The first part of the optimizer is done. It behaves more or less as described:


(defn optimize-forms-for [bitsprecision iter-forms other-forms squares?] ... )

user=> (optimize-forms-for 55 '[(:= x (* x z))] '[(:= y (+ y x))] false) ; Does nothing
[((:= x (* x z))) ((:= y (+ y x)))]
user=> (optimize-forms-for 55 '[(:= x (* z x x))] '[(:= y (+ y x))] false) ; Doesn't keep x^2 together.
[((:= x (* x (* z x)))) ((:= y (+ y x)))]
user=> (optimize-forms-for 55 '[(:= x (* z x x))] '[(:= y (+ y x))] true) ; Now does keep x^2 together.
[((:= x (* z (* x x)))) ((:= y (+ y x)))]
user=> (optimize-forms-for 55 '[(:= x (* z (/ a) x x (/ b)))] '[(:= y (+ y x))] true) ; Keeps reciprocals together.
[((:= x (* (* (/ a) (/ b)) (* z (* x x))))) ((:= y (+ y x)))]
user=> (optimize-forms-for 55 '[(:= x (* z (/ a) x x (/ b)))] '[(:= y (+ (* y q y) x))] true) ; Only keeps squares used for bailouts together.
[((:= x (* (* (/ a) (/ b)) (* z (* x x))))) ((:= y (+ (* y (* y q)) x)))]
user=> (optimize-forms-for 55 '[(:= x (* z (/ a) x x (/ b)))] '[(:= y (+ (* x q x) x))] true) ; CSE can combine the x^2s here.
[((:= x (* (* (/ a) (/ b)) (* z (* x x))))) ((:= y (+ (* q (* x x)) x)))]
user=> (optimize-forms-for 55 '[(:= x (* z (/ a) x x (/ b)))] '[(:= y (+ (* -1 q x) x (* -1 z) y))] true) ; Keeps negative terms together.
[((:= x (* (* (/ a) (/ b)) (* z (* x x))))) ((:= y (+ (+ (* -1 (* q x)) (* -1 z)) (+ x y))))]
user=> (optimize-forms-for 55 '[(:= x (* z (/ a) x x (/ b)))] '[(:= y (+ (* -1 q x) x (* -1 z) y k))] true) ; x and k stayed separated
[((:= x (* (* (/ a) (/ b)) (* z (* x x))))) ((:= y (+ (+ x y) (+ k (+ (* -1 (* q x)) (* -1 z))))))]
user=> (optimize-forms-for 55 '[(:= x (* z (/ a) x x (/ b) (+ x k)))] '[(:= y (+ (* -1 q x) x (* -1 z) y k))] true) ; Now x and k kept together
[((:= x (* (* z (+ x k)) (* (* x x) (* (/ a) (/ b)))))) ((:= y (+ (+ (* -1 (* q x)) (* -1 z)) (+ y (+ x k)))))]
user=> (optimize-forms-for 55 '[(:= x (* x y (/ (+ (* 3 y x z) 1)) z))] [] true) ; Groups the product xyz twice.
[((:= x (* (/ (+ (* 3 (* z (* y x))) 1)) (* z (* y x))))) ()]
user=> (optimize-forms-for 55 '[(:= x (* x y (/ (+ (* 3 y w z) 1)) z))] [] true) ; Misses an opportunity to factor out yz.
[((:= x (* (/ (+ (* 3 (* z (* y w))) 1)) (* z (* x y))))) ()]
user=> (optimize-forms-for 55 '[(:= x (+ x -1 (* x y (/ (+ a 1))))) (:= y (* 2 y (/ b) y (/ (+ a 1)) x))] [] true) ; Groups xy/(a + 1) for CSE in preference to keeping divisions together.
[((:= x (+ (* (/ (+ a 1)) (* x y)) (+ x -1))) (:= y (* 2 (* (/ b) (* y (* (/ (+ a 1)) (* x y))))))) ()]
user=> (optimize-forms-for 55 '[(:= x (* 3 x z))] '[(:= y (* 3 y z))] true) ; Here it misses the opportunity to factor out 3z, unfortunately.
[((:= x (* 3 (* x z)))) ((:= y (* 3 (* y z))))]
user=> (optimize-forms-for 55 '[(:= x (+ a (* 3 x)))] '[(:= y (+ b (* 3 x y)))] true) ; Here it doesn't though.
[((:= x (+ a (* 3 x)))) ((:= y (+ b (* y (* 3 x)))))]
user=> (optimize-forms-for 55 '[(:= x (+ a (* 3 x)))] '[(:= y (+ b (* 6 x y)))] true) ; It will even factor the 3x out of 6xy. Doesn't save a multiply though.
[((:= x (+ a (* 3 x)))) ((:= y (+ b (* 2 (* y (* 3 x))))))]
user=> (optimize-forms-for 55 '[(:= x (+ a (* 3 x) (* 2 y)))] '[(:= y (+ b (* 6 x y)))] true) ; This time it does!
[((:= x (+ (* 2 y) (+ a (* 3 x))))) ((:= y (+ b (* (* 3 x) (* 2 y)))))]
user=> (optimize-forms-for 55 (simplify-forms (real-forms *n-complex* '[(:= z (+ (** z 2) c))])) [] true) ; Standard M-set iteration gives usual result.
[((:= z-r (+ (* -1 (* z-i z-i)) (+ c-r (* z-r z-r)))) (:= z-i (+ c-i (* 2 (* z-i z-r))))) ()]
user=> (optimize-forms-for 55 (simplify-forms (real-forms *n-complex* '[(:= z (+ (** z 3) c))])) [] true) ; Cubic M-set iteration gives useful grouping of the squares.
[((:= z-r (+ (* z-r (* z-r z-r)) (+ c-r (* -3 (* z-r (* z-i z-i)))))) (:= z-i (+ (* -1 (* z-i (* z-i z-i))) (+ c-i (* 3 (* z-i (* z-r z-r))))))) ()]
user=> (optimize-forms-for 55
          (simplify-forms (real-forms *n-complex* '[(:= z (+ (** z 2) c))])) ; Distance estimator aux iteration added to normal M-set calc.
          (simplify-forms (real-forms *n-complex* '[(:= dz (+ (* 2 z dz) 1))])) true) ; Opportunity missed to group either (* 2 z-r) or (* 2 z-i).
[((:= z-r (+ (* -1 (* z-i z-i)) (+ c-r (* z-r z-r)))) (:= z-i (+ c-i (* 2 (* z-i z-r)))))
 ((:= dz-r (+ (* 2 (* dz-r z-r)) (+ 1 (* -2 (* dz-i z-i))))) (:= dz-i (+ (* 2 (* dz-r z-i)) (* 2 (* dz-i z-r)))))]


It does three things:

• groups multi-argument products and sums into chains of binary operations
• while remembering those binaries, preferentially extracting the same pairs from similar operations elsewhere in the same or another expression in the group so that CSE can save some ops;
• and when it can't do that, it tries to keep divided-by terms in products, or minus terms in sums, clumped so that a second pass, not yet implemented, can move the reciprocal/negation up the chain until there's only one, since tests have shown that divides and subtracts are more expensive than multiplies and adds respectively.

To do:

• Implement that second pass.
• Make it automatically filter its input through simplify-forms, and then through a new pass to extract common factors from sums.

I may also see if I can't pre-load the expressions to try to keep together by looking for common factors between pairs of sums and pairs of products using the common-factor-finding code. (THAT code has been written and tested, and is employed elsewhere, but isn't yet used in the optimizer.) That might get rid of many of the red entries above (where it failed to find CSE-optimization opportunities). The distance estimator case, in particular, could save two multiplies if the optimizer had a bit more brains under the hood.

I should have that done sometime tomorrow, and be on to other aspects of the job.

[cKleinhuis]

cool, perhaps you could try every known fractal formula ( atmost the large newtonian ones ) and provide optimized versions for them