So I was reading about
multiplicative calculus. And I thought that there might be an analog of the m-set in it.
After some trial and error, I came across the following formula:
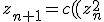^{(z_n^2)}))
Which does not have a additive critical point, but has three multiplicative critical points(i.e. it's geometric derivative equals 1 at three points): +/- 0.606530659712633 and 0.
The formula does have some issues, though. The first, obviously, is that it has multiple critical points. The second is that something is raised to z, which means that the fractal is bailout sensitive.
That being said, it does work:

A close up of the left side:

I'm going to try to find a function that has neither of those problems; however such a function is probably quite complicated!