Geometric Algebra, Geometric Calculus

[kram1032]

Cl(8,2) - "Double Conformal Geometric Algebra (or DCGA)" http://www.rxiv.org/pdf/1508.0086v1.pdf
Remember Cl(6,3)? (Qadratic Geometric Algebra or QGA) That was capable of representing all conic sections (but not in arbitrary rotations for certain objects)
Cl(8,2) goes one step further, also being able to represent a torus natively, and all its objects can be rotated arbitrarily (but not all objects can be intersected)
Perhaps allowing all intersections and in arbitrary rotations could be done with Cl(12,6) ("Double Quadratic Geometric Algebra") or Cl(12,3) or Cl(16,4) ("Triple" and "Quadruple Conformal Geometric Algebra) or similar such constructs. People still investigate this.
Perhaps we could even have a very systematic method to tackle in a computationally tractable manner, identifying arbitrary subspaces with the simplest possible polynomials that describe them, but that'll take a lot of thinking and analyzing still.

[hermann]

<a href="https://www.youtube.com/v/ItGlUbFBFfc&rel=1&fs=1&hd=1" target="_blank">https://www.youtube.com/v/ItGlUbFBFfc&rel=1&fs=1&hd=1</a>
A fascinating video of David Hestenes on his work with geometric algebra and geometric calculus the relations to physics and other parts of mathematics.
He also describes his truble on getting his importened work published.

Hermann

[kram1032]

nice, thanks for sharing! - I wish he'd go a little more in-depth with the actual operations though. This is hardly a "tutorial"

[hermann]

This thread has always been a great inspriration for me since I first read it the first time about two years ago.

During my physics study I was trained in vector analysis as the mathematics nessesarry for doing physics. It was a special course math for physics.

I was wondering if this is the complete story. I was told that if I had understood all the abstract math of the math courses that ran parallel all would become clear.
But this was not the case. I was thought a lot of abstract math where I often could not find the connection to physics.

Near the end of the math courses I asked the Professor of the relations between his lessons and physics he told me that he was a mathematician an had no deep understanding of physics and that his lesson was for mathematicians only. So I had been tought the wrong mathematics.

Nowdays I agree with the critics of modern mathematics (the mathematics I have been told) in the way that Norman Wildberger stated in some of his lectures:
http://wacker-art.blogspot.de/2016/01/why-infinite-sets-dont-exist.html

When I later tried to understand general theory of relativety I also discovered that the required maths had not been tought. I had to work my self through tensors and up and down indizies and was wondering if this had to be such complicate.

When I discovered geometric algebra here in Fractal Forums, this was an eye opener. This was the mathematics I was searching for.
I went through many of the papers posted in this thread that gave me a basic understanding of geometric algebra. I also started a geometric algebra page on my homepage in the internet.http://www.wackerart.de/mathematik/geometric_algebra.html

I then bought my first book on geometric algebra "Geometric Algebra for Physicists - Chris Doran Anthony Lasenby" which is an excellent book.
http://geometry.mrao.cam.ac.uk/2007/01/geometric-algebra-for-physicists/
As the title says it is an book for physicists and I have read some of the basic papers referenced in this thread. My favorit paper is still the one of Richard Allan Miller.
But with this preperation this is the right book to start digging deeper into physics. Many basic physics equations reveal more of there structure when written in the language of geometric algebra. So geometric algebra gives a clearer and easier access to physics, as if you know only the language of Gibb's Vector analysis.

This book also gave me a deeper understanding of geometric algebra.
Some of the chapters I have read several times and always discover something new.

Hermann

[kram1032]

Thanks for bringing up this website again!
Looks like Chris Dolan was actually holding a course on Geometric Algebra last year. - It was linked right there on the page where the book is promoted.
http://geometry.mrao.cam.ac.uk/2015/10/geometric-algebra-2015/
Each of those lectures also include slides. I'd imagine they match roughly with the book but I don't know: I haven't read it.

[hermann]

The slides of the lectures are close to the formulas in the book, so they give a good overview or may be used as a formular collection. But the book contains very much descriptive text, that makes it all understandable. The book covers much more topics then the slices of the lessons that are available. The lecture is mainly on the geometric algebra part of the book. Most of the physiks is not covered.

Hermann

[kram1032]

Well yeah, hopefully the book covers more than that

Found a new paper. This one is super abstract though. It's about how to extend Conformal Geometric Algebra to all kinds of spaces. - That is, ones over something other than real numbers. It'll work with

any field where the characteristic is not 2, and some of the constructions work even in that case.

A field of characteristic 2 is, for instance, something like integers modulo 2. If you multiply the multiplicative identity (1) with 2, in the integers modulo 2, you'll get back the additive identity (0).
So what they are saying is that for integers modulo 2 only parts of the construction work, but for integers modulo 3 and any field larger than that, this should work fine.
Some interesting infinitely large structures that should become possible with this are things like p-adic numbers, I think. Not entirely sure.

Here is the link: http://arxiv.org/pdf/1603.06863.pdf

[jehovajah]

https://m.youtube.com/watch?v=ItGlUbFBFfc
A fascinating video of David Hestenes on his work with geometric algebra and geometric calculus the relations to physics and other parts of mathematics.
He also describes his truble on getting his importened work published.

Hermann

For older platforms .

[hermann]

How to build Hypercomplex-Numbers from normal complex Numbers is done by the Cayley-Dickson Construction:
For details look at the following page John Baez:
http://math.ucr.edu/home/baez/octonions/node5.html

There is also an articel in Wikipedia:
https://en.wikipedia.org/wiki/Cayley%E2%80%93Dickson_construction

The History of Hyper Complex Numbers
http://history.hyperjeff.net/hypercomplex

Hermann

[hermann]

I have just watched the following video series on Geometric Calculus by Alan Macdonald.
It gives a very good Introduction to the basics of Geometric Calculus.

<a href="https://www.youtube.com/v/-JQxOYL3vhY&rel=1&fs=1&hd=1" target="_blank">https://www.youtube.com/v/-JQxOYL3vhY&rel=1&fs=1&hd=1</a>

An eye opener for people with basic knowledge on geometric algebra, vector analysis and complex analysis.
For me many of the things presented in this video series are well known.
But this videos shows very good how all works together.

Hermann

[kram1032]

That's actually a video series or two, one about GA, one about GC.
I'm glad these exist but I wish his style would be a little less "read-off-the-slides-y" and maybe more "hands on" if that makes sense?

[hermann]

Hallo Kram!  I have changed it from video to video series. Have you watched the whole series?

[kram1032]

yes, my comment applied to the series as a whole, not to just that one video
It's not a long series, so it's a fairly quick watch.

[jehovajah]

I have just watched the following video series on Geometric Calculus by Alan Macdonald.
It gives a very good Introduction to the basics of Geometric Calculus.

https://m.youtube.com/watch?v=-JQxOYL3vhY

An eye opener for people with basic knowledge on geometric algebra, vector analysis and complex analysis.
For me many of the things presented in this video series are well known.
But this videos shows very good how all works together.

Hermann

[macawscopes]

Apparently there are generalized 'Clifford algebras' that can be constructed from higher degree homogeneous polynomials.  From what  I can tell, these generalized 'Clifford algebras' have natural ternary, quartic, etc. operations instead of binary products.  

Ordinary Clifford algebras can be made by starting with the tensor algebra over a vector space, then sculpting it down using equivalence relations made between bivectors elements of the tensor algebra and corresponding scalars of a quadratic form.  

Say is a Clifford algebra of the quadratic form , then it has a binary product (a.k.a. the geometric product) .  The quadratic form is used to take the squares of grade-1 elements and equate them with scalars, e.g. , etc.  This is what trims down the geometric product and keeps it closed.

So... you can actually do something similar using algebraic forms, which are a generalization of quadratic forms.  A quadratic form is linked to a homogeneous quadratic polynomial.  Algebraic forms are linked to homogeneous polynomials of any degree, e.g. cubic forms

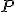
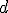
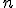
A homogeneous polynomial of degree in variables, can be thought of as a function .  This can be used in an analogous way to generate equivalence relations such as .  I've only seen papers about ternary ones,but I think theoretically you could create an n-ary algebra analogous to a Clifford Algebra from any homogeneous polynomial.

According to this paper, you cannot necessarily compose the ternary operation of a ternary algebra from repeated application of some binary operation.  So these things are fundamentally different from the familiar binary algebras.

I'm still scratching my head on how to actually formulate these things.  But it's starting to make more sense as time goes on....

One clue is here.  A symmetric tensor is the analog of a symmetric matrix, and it is decomposable in an analogous way to how symmetric matrices are diagonalizable.  Wikipedia says that: "The space of symmetric tensors of order r on a finite-dimensional vector space is naturally isomorphic to the dual of the space of homogeneous polynomials of degree r on V"...  which I translate to mean that for every homogeneous polynomial of degree r on V, there is a unique symmetric tensor of order r.

Here is the scoop on decomposition of symmetric tensors

Do a search for "ternary clifford algebra" and see what you come up with.  There are quite a few papers on it, though most of them are really, really hard to understand.

Obviously, I'd love to make fractals out of these things!