Geometric Algebra, Geometric Calculus

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #150 on: November 08, 2014, 04:13:25 PM »

Ok, digging through Garret Sobczyk's older papers, I figured this out a bit more, though I'm still not entirely sure how it works.
His whole point is that, using his propsed basis of idempotents and nilpotents - the "generalized spectral basis" -, the product table simplifies itself a lot.

For instance, if I'm not mistaken (calculated all those myself) here are all of his proposed nilpotents and idempotents in the Clifford-Algebra with signature $\left{2,0,0\right}$ :

$s1_\phi = s1_\phi^2 = \frac{1}{2} \left( 1 + x \cos{\phi} + y \sin{\phi} \right) \\ s2_\phi = s2_\phi^2 = \frac{1}{2} \left( 1 - x \cos{\phi} - y \sin{\phi} \right) \\ s1_\phi s2_\phi = 0 \\ s1_\phi + s2_\phi = 1 \\ q1_\phi = s1_\phi q1_\phi = r \left(x \sin{\phi} + y \cos{\phi} + i \right) \\ q2_\phi = s2_\phi q2_\phi = r \left(x \sin{\phi} - y \cos{\phi} + i \right) \\ q1_\phi^2 = q2_\phi^2 = 0 \\ q1_\phi q2_\phi = 2 r^2 \left(\sin{\phi}^2-\left(x+i \sin{\phi} \right)\cos{\phi}\right)$

All but the very last one of those are rather pretty. I'm not quite sure what to make of that last one. Here's a multiplication table:

$\begin{array}{ccccc} 1 & s_1 & s_2 & q_1 & q_2 \\ s_1 & s_1 & 0 & q_1 & s_1 q_2 \\ s_2 & 0 & s_2 & s_2 q_1 & q_2 \\ q_1 & q_1 & q_1 s_2 & 0 & q_1 q_2 \\ q_2 & q_2 s_1 & q_2 & q_2 q_1 & 0 \end{array}$

I didn't yet try out all of those. All of those which have two terms in them should, according to Sobczyk, either cancel to 0 or become one of the original terms. That's why I'm a little confused by the rather strange-looking form of $q_1 q_2$ , though it might be that I'll actually have to give up some more generality, fixing either the $\phi$ or the $r$ or perhaps both to get to that especially nice form. Still reading to figure that out.
Speaking of generality: for all four terms, $\begin{array}{cccc}s_1 & s_2 & q_1 & q_2\end{array}$ , I started with a general object containing all base- $p$ -vectors, so if something is missing, it's because some condition on those objects requires that it is 0.


« Last Edit: November 08, 2014, 04:27:02 PM by kram1032 »	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #151 on: November 10, 2014, 08:58:08 PM »

I appear to have miscalculated $q_1 q_2$ . It actually becomes $-2r^2 \cos\phi \left(x+e^{i \phi}\right)$ and the product $q_2 q_1 = 2r^2 \cos\phi \left( x-e^{-i \phi}\right)$ and $q_1$

Meanwhile, $\left(q_1 q_2\right)\left(q_2 q_1\right) = 4 r^4 \sin{2\phi} \left(\sin\phi - y\right)$ ?
I must be doing something wrong because, if that is true, associativity would no longer hold, which would be kinda awkward. Quite clearly, from $q_2^2=0$ , $\left(q_1 q_2\right)\left(q_2 q_1\right) = q_1\left(q_2^2\right)q_1 = q_1 0 q_1 = 0 \neq 4 r^4 \sin{2\phi} \left(\sin\phi - y\right)$ ...
Does anybody see where my error lies?


	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #152 on: November 12, 2014, 12:51:37 AM »

Ok, things are more complicated than I thought they would be.
While $s_1 q_1 = q_1$ , it is not true, that $s_1 q_1 = q_1 s_1$ . Thus, we are in the weird situation, where $s_1$ acts as some kind of non-commutative unity. That's quite like if $1 a = a \neq a 1$ .

However, I can't actually find references in Garret Sobczyk's works, where he actually uses the nilpotents $q$ in his GA basis. They don't appear to always occur or, more accurately, they often appear to just be $0$ . So perhaps this actually is an instance of that.
In particular, if I require $s_1 q_1 = q_1 = q_1 s_1$ , that requires me to set $r=0$ , so $q_1 = 0$ .
In that case I actually only have to deal with the idempotents $s$ and the entire product-table becomes:

$\begin{array}{ccc} 1 & s_1 & s_2 \\ s_1 & s_1 & 0 \\ s_2 & 0 & s_2 \end{array}$

Interestingly, while $M s1 \neq s_1 M$ and $M s_2 \neq s_2 M$ , it still is true that $M s_1 + M s_2 = s_1 M + s_2 M = M$ .
This is an important property. It, for instance, means, that $M^k = (M s_1 + M s_2)^k = (M_1 s_1 + M_2 s_2)^k = M_1^k s_1 + M_2^k s_2$ (for some arbitrary Multivector $M$ )
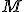
and through applying this idea to a Taylor series, that also means that $f\left(M\right) = f\left(M_1 s_1+M_2 s_2\right) = f\left(M_1\right) s_1 + f\left(M_2\right) s_2$ . This is what makes this basis so powerful. - Assuming you can easily find the value of a given function at $M_{1,2}$ , you can easily calculate any function at some general M.

That's all assuming that I got that right and the $q$ s are indeed 0 for this problem. If they actually are not, that means a general function would somehow use them.

A bit more explanation:
Since idempotents have the following propery: $s^2=s$ , they act as projectors. i.e. if you multiply something with them muliple times, that thing will no longer change. $M s s ... s = M s = M' s$ - that's what I used above when I said $M s_1 = M_1 s_1$ . The very first product changes things around, but every further product doesn't change a thing.
Similarly, since $s^2=s$ implies $s^k=s$ and something of the form $\left( a_1 s_1 + a_2 s_2\right)^k$ will produce some form that has every combination $s_1^i s_2^(k-i)$ , we get, for all those terms, except for when $i =0$ or $i=k$ , simply the replacement term $s_1 s_2$ . This term, however, by the properties of our special idempotents, is $0$ . Thus only the two terms with the highest powers remain. Those two leftover terms reduce to $s_1$ and $s_2$ respectively.
If you put all this into a taylor series, you'll get the above result, that any analytic function can be expressed by $f\left(M\right) = f\left(M_1 s_1+M_2 s_2\right) = f\left(M_1\right) s_1 + f\left(M_2\right) s_2$ .

Lastly, there is one more weird thing about these idempotents:
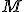
$s_1 M s_1$ would be the "reflection" of $M$ in $s_1$ . I put that in "quotation marks", because it only really would be a reflection if I used pure vectors, and I obviously am using vectors with a scalar part here.
This reflection completely knocks out the bivector part. Furthermore, no matter what side you multiply $s_1$ onto that product, the result will no longer change:
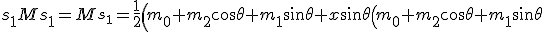$s_1 M s_1 = M_{s_1} = \frac{1}{2}\left(m_0+m_2\cos\theta+m_1\sin\theta + x \sin\theta \left(m_0+m_2\cos\theta+m_1\sin\theta\right) + y \cos\theta \left(m_0+m_2\cos\theta+m_1\sin\theta\right)\right)$
So for this value, "reflection" and projection kind of coincide. I wonder about the exact geometric interpretation of this.


	Logged

jehovajah

Global Moderator
Fractal Senior

Posts: 2749

May a trochoid in the void bring you peace

Re: Geometric Algebra, Geometric Calculus

« Reply #153 on: November 12, 2014, 09:30:26 AM »

Thanks for the links. Kram1032. I have added them to my collection of links on this topic.

I find Norman Wildberger a good source for most of these fundamentals of the topic. I like to look at the different presentations though because it gives me some alternative views on the meaning or possible interpretation of Hermann Grassmanns Labels or Handles or Notions(Begriffe).

Keep up the good Work and wishing you success in your studies and research.

Hermann I also thank you for your interest and contribution. The issue of visualisation and dimensions is a tricky one. Currently I go with crystal spaces and facets as realisations of multidimensional extensive magnitudes. I am a big Scirnce fiction fan, but draw the line when it comes to hidden other worldly dimensions.

Hey, anything is possible, right? certainly the fractal generator allows us to tour a fractal in all these possible dimensioned spaces, with boundaries materialising and dematerialising as we go, but pragmatically I do not have time to figure out other solutions. Confusing as it is I just make do with interleaving crystal spaces.

V9 and V18 are an attempt to understand the geometrical model underpinning Vortex Based Mathrmatics as exposited by Randy Powell. I was and am curious to see what a fractal generator makes of it. I was encouraged somewhat by my design of Newtonian Triples, where the dimensions were directly manageable by a quaternion framed fractal generator.

However, since I did not understand or rather "everyway stand" what I was doing I thought it best to get to grips with Hermann Grassmanns methods and prior to that Hamiltons. What a treat that has turned out to be!

Yes I will eventually finish the V9 " *" table and the V18, but I want to know what the Fractsl images might relate to in magneto dynamics , say, not only just for the hopefully beautiful forms!


« Last Edit: November 12, 2014, 10:19:02 AM by jehovajah »	Logged

May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!

jehovajah

Global Moderator
Fractal Senior

Posts: 2749

May a trochoid in the void bring you peace

Re: Geometric Algebra, Geometric Calculus

« Reply #154 on: November 12, 2014, 10:27:17 AM »

Actually it just came back to mind. I remember setting Laz Plaths, aka qqazxxsw on YouTube , trochoid applications as my favourite visualisation tools! You can set up an n dimensional trochoid very easily and intuitively on his apps, because each rotating circle represents a dimension.

Check out his channel and videos. Count how many circles he uses!

I honestly think this man has solved the problem of visualising n dimensions in every practicable way. But he won't talk to me!

Oh well, that's life I suppose cheesy


« Last Edit: April 11, 2015, 11:53:48 PM by jehovajah »	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #155 on: November 23, 2014, 07:23:21 PM »

Spacetime Algebra for Electromagnetism


	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #156 on: December 04, 2014, 02:14:21 PM »

I'm not sure if I already linked this paper here (slowly but surely the thread becomes kinda long to check every single post)
Geometric Algebra - Reformulation of General Relativity - this one will obviously not be suitable for beginners: Even if GA is able to simplify geometric formulations, or rather, it adds nice geometric insight in abstract algebraic formulae, GR is so abstract, it'll take getting used to in any kind of formulation.

That being said, I personally, having at least a vague idea of tensor calculus, can follow at the very least the first section (Everything up to and including the part where they solve the Schwarzschild-Metric) with some success. The most difficult bit is getting used to the billions of symbols. But once you accept their meaning, it's fine.


« Last Edit: December 04, 2014, 03:40:37 PM by kram1032 »	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #157 on: January 17, 2015, 12:58:01 PM »

Here are the slides and exercises for a complete course about Computing with Geometric Algebra http://www.gaalop.de/ga-computing-lecture/

It's by the guy behind the Gaalop Geometric Algebra package (hence the website), who also works at TU Darmstadt.

EDIT: apparently the slides are a mixture of English and German.


« Last Edit: January 17, 2015, 01:26:30 PM by kram1032 »	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #158 on: January 27, 2015, 10:27:14 AM »

A new approach to euclidean plane geometry based on projective geometric algebra


« Last Edit: January 27, 2015, 10:29:57 AM by kram1032 »	Logged

jehovajah

Global Moderator
Fractal Senior

Posts: 2749

May a trochoid in the void bring you peace

Re: Geometric Algebra, Geometric Calculus

« Reply #159 on: January 27, 2015, 10:30:52 PM »

Thanks for the link Kram1032. wink


	Logged

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #160 on: February 17, 2015, 03:02:06 PM »

I've read a lot about a general Multivector not having an inverse and it not being possible to define one.
However I played around and found a way for at least the normal positive signature $\mathbb{R}^3$ -case. If you just want the formula, jump to the end. What follows is an explanation of how I arrived at the result (plus background you probably already know if you follow this thread. I wanted to make this post fairly self-contained).

To define an inverse for complex numbers, what you have to do is this:
$\frac{1}{z}=\frac{z^*}{z z^*} = \frac{z^*}{{\left|z\right|}^2}$

Essentially, to find a division, you have to figure out a way to make the denominator a real number just by multiplying numbers which are equal to 1.
In case of the complex number above, what you have to do is multiply by $1=\frac{1}{1} = \frac{z^*}{z^*}$ , requiring a single multiplication to get to the desired result.

Now, it indeed doesn't appear to be possible to do a single multiplication to get to a real number (i.e. a pure scalar) but multiple multiplications do the trick.

First, let me define a few short-hand notations:

You can write a Multivector $\in \mathcal{Cl}\left(\mathbb{R}^3\right)$ in one of the following equivalent notations: $M=\left(a,\mathbf{x},\mathbf{B} i,c i\right)=\left(a,\left(x_1,x_2,x_3\right),\left(B_1,B_2,B_3\right) i,c i\right) = \\ a+x_1 e_1 + x_2 e_2+x_3 e_3 + B_1 e_2 e_3 + B_2 e_3 e_1 + B_3 e_1 e_2 +c e_1 e_2 e_3 = \left(\left(a+c i\right)+\left(x_1+B_1 i\right)e_1+\left(x_2+B_2 i\right)e_2+\left(x_3+B_3 i\right)e_3\right) = \\ \left(a+i c,\mathbf{x}+i\mathbf{B}\right) = \left(a+i c,\left(x_1+i B_1,x_2+i B_2,x_3+i B_3\right)\right)$

For convenience's sake, I'll be using the second to last notation.
I'll furthermore introduce the shorthand $a+i c = \alpha \in \mathbb{C}$ and $\mathbf{x}+i \mathbf{B} = \mathbf{\nu} \in \mathbb{C}^3$
So then my general Multivector becomes $M=\left(\alpha,\mathbf{\nu}\right)$

Although $i$ here is technically a shorthand for $e_1 e_2 e_2$ , in the following it can be treated exactly like the familiar imaginary unit.

$\mathbf{x} \cdot \mathbf{y}$ is the normal (real) dot product. (Do not conjugate complex numbers)
$\mathbf{x} \times \mathbf{y}$ is the normal cross product.
The wedge product $\mathbf{x} \wedge \mathbf{y} := i \mathbf{x} \times \mathbf{y}$

The Geometric Product of two Multivectors $M,N$ is defined as follows:
$M N = \left(\alpha_M \alpha_N+ \mathbf{\nu}_M \cdot \mathbf{\nu}_N,\alpha_M \mathbf{\nu}_N+\alpha_N \mathbf{\nu}_M+i \left(\mathbf{\nu}_M \times \mathbf{\nu}_N \right)\right)$

Then there is the Flip operation which simply switches the sign of the vector part:
$\text{Flip }{M} =M^F = {\left(\alpha,\mathbf{\nu}\right)}^F =\left(\alpha,-\mathbf{\nu}\right) = \left(a+i c,-\mathbf{x}-i\mathbf{B}\right)$
and the Conjugate, which switches the sign of the imagnary part:
$\text{Conjugate }{M} = M^* = {\left(\alpha,\mathbf{\nu}\right)}^* =\left(\alpha^*,\mathbf{\nu}^*\right) = \left(a-i c,\mathbf{x}-i\mathbf{B}\right)$

Ok, with all this we can finally define inversion:
$\frac{1}{M} = \frac{1}{M} \frac{M^F}{M^F} = \frac{1}{M} \frac{M^F}{M^F} \frac{\left(M M^F\right)^*}{\left(M M^F\right)^*} = \frac{M^F \left(M M^F\right)^*}{M M^F \left(M M^F\right)^*$

For this last fraction, the denominator is indeed real-valued. The given inverse is both a left- and a right-inverse, so no special care has to be taken for the order.
I.e. $\for_{M}: M \frac{1}{M} = \frac{1}{M} M = 1$

Finally, here is the result expanded in full component form (no longer with real denominator, but as said, you can treat $i$ like you would treat any complex number):

$\frac{1}{M} = \left(a+i c,\left(-x_1-i B_1,-x_2-i B_2,-x_3-i B_3\right)\right) \frac{1}{{\left(a+i c\right)}^2-\left({\left(x_1+i B_1\right)}^2+{\left(x_2+i B_2\right)}^2+{\left(x_3+i B_3\right)}^2\right)}$

Obviously, there are some problems with multivectors for which ${{\left(a+i c\right)}^2-\left({\left(x_1+i B_1\right)}^2+{\left(x_2+i B_2\right)}^2+{\left(x_3+i B_3\right)}^2\right)}=0$ . These are the null multivectors for which division is indeed undefined.


	Logged

hermann

Iterator

Posts: 181

Re: Geometric Algebra, Geometric Calculus

« Reply #161 on: April 05, 2015, 03:54:09 PM »

The Geometric Algebra Homepage at Cambridge University has a new layout. It worth visiting it!
http://geometry.mrao.cam.ac.uk/
Sadly, I personaly have not much time to work further on geometric algebra but have bought the book Geometric Algebra for Physicsts from Doran/Lasenby and stated reading it.
Being familiar with physics and basics of geometric algebra it is worth reading it!

Hermann


	Logged

Hermann
http://www.wackerart.de

kram1032

Fractal Senior

Posts: 1863

Re: Geometric Algebra, Geometric Calculus

« Reply #162 on: April 09, 2015, 06:02:41 PM »

I found another wikipedia page which I think wasn't mentioned in this thread before

https://en.wikipedia.org/wiki/Plane_of_rotation

This one isn't about geometric algebra per se but rather about the concept of rotation in arbitrary numbers of dimensions (featuring the iconic rotating hypercube). It does, however, illustrate how geometric algebra is very useful in describing the notion of rotation and gives a different angle on bivectors (introducing them as rotation rather than "twodimensional" vectors that later are identified as rotations)


	Logged

flexiverse

Safarist

Posts: 99

Re: Geometric Algebra, Geometric Calculus

« Reply #163 on: April 10, 2015, 02:21:08 AM »

Very interesting this. Having just learnt how important grassmanian algebra is.

What is the best resource to Learn clifford algebra for absolute beginners ?

I always thought there should be a more unified algebra that works in all dimensions! I'm completely mind blown grassmann was doing this so long ago !!!


	Logged

flexiverse

Safarist

Posts: 99

Re: Geometric Algebra, Geometric Calculus

« Reply #164 on: April 10, 2015, 02:30:03 AM »

Quote from: jehovajah on November 12, 2014, 10:27:17 AM

Actually it just came back to mind. I remember setting Laz Plaths, aka qquazxxsw on YouTube , trochoid applications as my favourite visualisation tools! You can set up an n dimensional trochoid very easly and intuitively on his apps, because each rotating circle represents a dimension.

Check out his channel and videos. Count how many circles he uses!

I honestly think this man has solved the problem of visualising n dimensions in every practicable way. But he won't talk to me!

Oh well, that's life I suppose cheesy

Er, I can't find qquazxxsw on you tube ?


« Last Edit: April 11, 2015, 11:48:48 PM by jehovajah »	Logged

Pages: 1 ... 9 10 [11] 12 13 ... 15 Go Down

« previous next »

	Author	Topic: Geometric Algebra, Geometric Calculus (Read 12372 times)
		Description:
0 Members and 1 Guest are viewing this topic.

Related Topics
	Subject	Started by	Replies	Views	Last post
	geometric spirals Mandelbulb3D Gallery	bib	0	867	October 25, 2010, 09:48:32 PM by bib
	Geometric Buddha Images Showcase (Rate My Fractal)	John Smith	0	1030	June 07, 2012, 09:05:17 PM by John Smith
	Retro Geometric Still Frame	FracZky	0	1177	May 02, 2013, 07:30:42 PM by FracZky
	Geometric Patterns No. 2 Saturn&Titan Gallery	element90	2	891	February 09, 2014, 03:43:35 PM by Dinkydau
	Geometric Fractals Help Help & Support	lancelot	13	910	December 15, 2014, 06:10:29 PM by Sockratease

END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

it was a great time but no longer maintainable by c.Kleinhuis contact him for any data retrieval,
thanks and see you perhaps in 10 years again

The All New FractalForums is now in Public Beta Testing! Visit FractalForums.org and check it out!

	Welcome, Guest. Please login or register.	April 19, 2024, 08:25:15 PM
		Login with username, password and session length

END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

it was a great time but no longer maintainable by c.Kleinhuis contact him for any data retrieval, thanks and see you perhaps in 10 years again

The All New FractalForums is now in Public Beta Testing! Visit FractalForums.org and check it out!

it was a great time but no longer maintainable by c.Kleinhuis contact him for any data retrieval,
thanks and see you perhaps in 10 years again