(accidentally posted early, still editing, come back a bit later)
The classic (pre-bulb) extension of the Mandelbrot-Set used to be based on Quaternions, since those are a fairly straight-forward extension of complex numbers.
However, there is another extension, that, in the "1-Dimensional" case (where we deal with complex numbers as dimensions) reduces to the complex numbers of norm 1. That would be the unitary group.
The unitary group has multiple parametrizations, one of which is:
}{\sqrt{\cos (2 p)+3}} & -\frac{2 e^{i r} \sin ^2\left(\frac{p}{2}\right)}{\sqrt{\cos (2 p)+3}} \\ \frac{2 e^{i s} \sin ^2\left(\frac{p}{2}\right)}{\sqrt{\cos (2 p)+3}} & \frac{2 e^{i (-q+r+s)} \cos ^2\left(\frac{p}{2}\right)}{\sqrt{\cos (2 p)+3}}<br />\end{array}<br />\right))
with
\in \mathbb{R})
.
I chose this parametrization, to make it easy to solve for the various variables. In this form, q, r and s are just phases, while the factors that involve p are between 0 and 1. There are more beautiful parametrizations, however, they make it harder to solve for p, because they are between -1 and 1 and thus mix with the three complex phases, making the seperation more complicated.
Despite that , I still have four different possible values for p after squaring. Solving for the other things isn't as hard.
The main issue I have is that some of the expressions will not reduce all too nicely
Here you go, for the squared case:
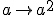
![p\to \left( 2 \tan ^{-1}\left(\frac{\sqrt{2} |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{(\cos (2 p)+3)^2-4 \sin ^4(p) \cos^2\left(q-\frac{r}{2}-\frac{s}{2}\right)}}\right) \vee -2 \tan ^{-1}\left(\frac{\sqrt{2} |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{(\cos (2 p)+3)^2-4 \sin ^4(p) \cos ^2\left(q-\frac{r}{2}-\frac{s}{2}\right)}}\right)\vee -2 \tan ^{-1}\left(\frac{2 |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{-8 \sin ^4(p) \cos (2 q-r-s)+28 \cos (2 p)+\cos (4 p)+35}}\right)\vee 2 \tan^{-1}\left(\frac{2 |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{-8 \sin ^4(p) \cos (2 q-r-s)+28 \cos (2 p)+\cos (4 p)+35}}\right) \right)](/cgi-bin/mimetex.cgi?p\to \left( 2 \tan ^{-1}\left(\frac{\sqrt{2} |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{(\cos (2 p)+3)^2-4 \sin ^4(p) \cos^2\left(q-\frac{r}{2}-\frac{s}{2}\right)}}\right) \vee -2 \tan ^{-1}\left(\frac{\sqrt{2} |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{(\cos (2 p)+3)^2-4 \sin ^4(p) \cos ^2\left(q-\frac{r}{2}-\frac{s}{2}\right)}}\right)\vee -2 \tan ^{-1}\left(\frac{2 |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{-8 \sin ^4(p) \cos (2 q-r-s)+28 \cos (2 p)+\cos (4 p)+35}}\right)\vee 2 \tan^{-1}\left(\frac{2 |\sin (p)| \sqrt{\left|\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right|}}{\sqrt[4]{-8 \sin ^4(p) \cos (2 q-r-s)+28 \cos (2 p)+\cos (4 p)+35}}\right) \right))
(where
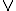
is the symbol for "or", so it's one of the four possibilities. If you were to plot them, you'd see that they are different in just their phase and sign. They are almost the same functions)
-8 \sin ^4\left(\frac{p}{2}\right) e^{i (r+s)}}{\sqrt{-8 \sin ^4(p) \cos (2 q-r-s)+28 \cos (2 p)+\cos (4 p)+35}}\right))
 \text{sgn}\left(\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right))
 \text{sgn}\left(\cos \left(q-\frac{r}{2}-\frac{s}{2}\right)\right))
this works in four complex dimensions:
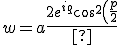}{\sqrt{\cos (2 p)+3}}+c_1)
}{\sqrt{\cos (2 p)+3}}+c_2)
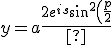}{\sqrt{\cos (2 p)+3}}+c_3)
 e^{i (-q+r+s)}}{\sqrt{\cos (2 p)+3}}+c_4)
Since all of those are complex numbers, you also can use four complex constants rather than real ones.
This still needs a bit of work, particularly, I haven't yet shown the inverses for the last four functions yet, which are the actual iteration functions, but it's late now. If anyone is willing to test out this right now admittedly rather messy set, it shouldn't be too hard to find the corresponding inverses.
You'd first have to convert from w, x, y, z to a, p, q, r, s, then replace the four by their squared analogues, then back-convert to w, x, y, z and add constants. This is directly analogous to how you'd do it with any mandelbulb variant, converting between polar and rectangular coordinates.
I'm not sure how best to visualize it as it's effectively an 8-dimensional space to search, but trying out all the major planes sure is a good start.


















