If you want to go after those amplitude formulae, I suggest you collect all constants into one big term.
For instance, G is the gravitational constant and c is the speed of light. You might as well set both to 1 or you can artistically modify them.
R, if you want to keep it correct, would be a parameter giving the distance of the camera from the center of mass of the two orbiting mass - points. For a steady camera, this is a constant.
r is the distance between the two objects in question. This is another constant
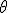
gives the angle between the observer and the plane of the rotation, starting from the center of mass.
You have to slightly transform that angle so it becomes what you'd usually think of as spherical coordinates.

is the angular velocity. It's how fast the two masses orbit each other.
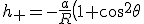\cos\left(2\omega\left(t-R\right)\right)<br />h_\times = -\frac{2a}{R} \left(\cos\theta\right)\sin\left(2\omega\left(t-R\right)\right))

contain all the constants, like the masses and the gravitational constant.
This is essentially, how easy those formulae can get. The dependency of the amplitude in the z-direction is governed by
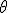
. In the x-y-plane, the wave's amplitude is radially symmetric and given by
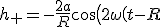\right)<br />h_\times = -\frac{2a}{R} \sin\left(2\omega\left(t-R\right)\right))
Note how this amplitude drops over distance and how the frequency changes both over distance and time, increasing with time, decreasing with distance.
On the point where the distance equals the time, the frequency becomes 0. This is simply where you travel away from the center of mass at the speed of light.
If you actually want to use this for producing 3D static fractals, you probably don't want a time dependency or an amplitude drop. So in that case, you should modify those formulae to:
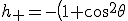\cos\left(2\omega R \right)<br />h_\times = \cos\left(\theta\right)\sin\left(2\omega R \right)<br />)
In this geometric setup,
=sqrt{R^2-z^2})
, so
=z)
and
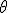
may only vary between

.
Essentially you could just use (a 3D version of) my swirl transform and put the two formulae in front of it as an amplitude. For the most general state, I think you would just use a super-position of the two formulae:
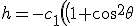\cos\left(2\omega R \right)\right)+c_2\left(\cos\left(\theta\right)\sin\left(2\omega R \right)\right))
where
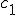
and
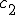
should probably be normalized.
I'm not entirely sure if that's how you're supposed to use them though. You could always just try to use one of them. The difference apparently is how the gravitational waves would distort masses:

versus



Technically, the two could also be superposed out of phase (e.g. with different times, rather than both synced up), which would cause more complex patterns.