How to recognize the holy grail fractal?

[mfg]

Have you passed by the holy grail fractal but did not recognize it?

maybe ...

On the other hand, have you thought (or felt, or even were sure) that you found it and then it somehow vanished ...

There have been several topics posted in this forum pertaining these questions. In particular, fracmonk proposed eight properties that M-like sets should fulfill. More recently kjknohw mentioned four. Daniel White asks whether the mandelbulb produced with triplex algebra is the real McCoy (or McKay) - his answer is close to the real one but not it (why?).

To some fractalists the property of connectedness is crucial whereas to some others it is not as important. As David Makin points out with precious intuition, “anything that is disconnected in n dimensions can become connected in n+1 (or higher) dimensions“

I will try to review the fundamental properties that a discrete fractal set should fulfill. In the process, I hope that we will achieve a minimum consensus regarding the essential properties, the desirable ones and those that are unimportant or irrelevant. Within the crucial (essential) ones some criteria will be necessary to establish breath-taking highlights from standard ones.

[Tglad]

In my opinion, the most important property of the 2d Mandelbrot set is that it is universal.
http://www.math.harvard.edu/~ctm/papers/home/text/papers/muniv/muniv.pdf
None of the 3d variants get close to this property.

[s31415]

To Tglad: How would you generalize the universal property described in the article to higher dimension? The 3-sphere is obviously not a complex manifold, so you cannot define families of holomorphic maps from X x S^3 to S^3. One might be tempted to replace "holomorphic" by "conformal", as this is equivalent for maps on the 2-sphere. However this is changing the definition of the article, as a family of conformal maps from X x S^2 to S^2 is not the same as a family of holomorphic maps from X x S^2 to S^2...

To mfg: This has been already stated in many posts, but maybe it's worth recalling... The fundamental reason why there is no equivalent of the Mandelbrot set in 3d is that the group of conformal transformations is much smaller in 3d. In particular, there is no equivalent to the 2-to-1 conformal transformation z -> z^2. This doesn't mean that it's not worth exploring 3d iterated transformations, as this exploration yielded a lot of interesting 3d fractals. Just don't expect to find an equivalent of the Mandelbrot set.

Best,

Sam

[Tglad]

I'm pretty sure that being universal means that you can rotate, scale and translate the mandelbrot every iteration and you still end up with the mandelbrot set (just rotated, scaled and translated in some way). i.e. z = (z^2 + c) * d + e is a mandelbrot set for any complex d, e.
This idea could extend to 3d. But I agree that it is most likely impossible to do in 3d, and I'm also sure there is no direct 3d mandelbrot set.
But maybe in some 11 dimensional non-euclidean space, under some unusual algebra rules... something equally interesting lurks.

[s31415]

Insert Quote
I'm pretty sure that being universal means that you can rotate, scale and translate the mandelbrot every iteration and you still end up with the mandelbrot set (just rotated, scaled and translated in some way). i.e. z = (z^2 + c) * d + e is a mandelbrot set for any complex d, e.

This looks indeed a special case of the theorem, when X is C^3 and parameterized by (c,d,e). Although he's not quite proving that what you get is a Mandelbrot set. He just says that minibrots are dense in this set. (Provided "small Mandelbrot sets" is the same as minibrots, he doesn't seem to define what he means by small.)

[Syntopia]

Insert Quote
I'm pretty sure that being universal means that you can rotate, scale and translate the mandelbrot every iteration and you still end up with the mandelbrot set (just rotated, scaled and translated in some way). i.e. z = (z^2 + c) * d + e is a mandelbrot set for any complex d, e.

This looks indeed a special case of the theorem, when X is C^3 and parameterized by (c,d,e). Although he's not quite proving that what you get is a Mandelbrot set. He just says that minibrots are dense in this set. (Provided "small Mandelbrot sets" is the same as minibrots, he doesn't seem to define what he means by small.)

I think it is difficult to tell from the paper, what exactly it is meant by 'universality'. I have seen the term used differently, as is 'the Mandelbrot set will appear in many mappings': http://classes.yale.edu/fractals/Mandelset/MandelUniversality/QLMaps.html

But the Mandelbrot set invariance under inner translations, rotations, and scalings, is easy to test visually. I remember first time I read about it (in another post by Tglad), and I had to test it to be convinced. To me it is a quite striking property.

The problem is that this invariance eats most of the conformal 3D transformations, leaving only sphere inversions and reflections. Which are the core transformations for the Mandelbox, but the Mandelbox is not invariant under the other transformations. Still it might be possible to find a conformal and universal (in the inner translation/rotation/scaling invariance sense) 3D fractal, perhaps through some creative use of conditional transformations.

[s31415]

Still it might be possible to find a conformal and universal (in the inner translation/rotation/scaling invariance sense) 3D fractal, perhaps through some creative use of conditional transformations.

I doubt it. The fractal properties of the Mandelbrot set rely crucially on two properties:
- The fact that the underlying map is conformal. This ensure that the small scale structures are not stretched and stay recognizably 2-dimensional, instead of turning into "whipped cream"...
- The fact that there exists a conformal transformation which is 2 to 1 (or many to one). This is absolutely necessary in order for the orbits to merge at each iteration thus creating self-similarity. You will never create a fractal with a Mandelbrot-like algorithm with just 1 to 1 transformations. (Try iterating Moebius transformations, for instance.)

The point is, there is no conformal 2 to 1 transformation of the 3-sphere. The kaleidoscopic IFS (and also the Mandelbox if I remember well) get away with this by iterating "almost conformal" transformations, i.e. transformations that are conformal everywhere except on some lower dimensional locus (in the case of kaleidoscopic IFS, this locus is the location of the mirrors). There are almost conformal transformations that are 2 to 1, which allows the existence of such fractals, but there are no honest conformal transformations that are 2 to 1 or many to 1. This prevents the construction of unstretched fractals that are free of local mirror symmetries, which I guess would be my lowest criterion for a 3d analogue of the Mandelbrot set. A "creative use of conditional transformations" means for me finding other types of almost conformal transformations, which would definitely be interesting, but would not produce something I could call a 3d M-set.

Anyone aiming at finding a 3d M-set should think seriously about the difficulty above. I think it is unavoidable, but of course I might be wrong...

[David Makin]

I personally believe that the universality of the complex Mandelbrot stems from the fact that complex numbers are a mathematical field.
I think it has been proved conclusively that there is no true field in R3 and it seems (at least based on what I know of 4D e.g. quaternions/hypercomplex) that there is no true field in 4D and probably not in any higher number of dimensions *but* I don't think this has been proved conclusively for Rn where n>3 and definitely not for all n>4, though of course intuitively the constraints of higher dimensional systems mean that the higher the dimension then the more the requirements for a true field fail to hold true.
However even having said that, it doesn't mean that we can't find very strange beasts that will produce a universal Mandelbrot with Rn, n>=3 , if the normal mathematical rules are extended/manipulated more than usual e.g. say such that a power of a dimension beyond the second is always used, or even say log or some other function etc.
Edit:
Just realised that last bit is essentially exactly what Tglad said i.e."But maybe in some 11 dimensional non-euclidean space, under some unusual algebra rules... something equally interesting lurks."

[Syntopia]

I think these theorems says you won't find nice division algebras (and hence no field containing the reals) in any higher-dimensional space:
http://en.wikipedia.org/wiki/Frobenius_theorem_%28real_division_algebras%29
http://en.wikipedia.org/wiki/Normed_division_algebra

On the other hand I'm not sure why division should be necessary.

A "creative use of conditional transformations" means for me finding other types of almost conformal transformations, which would definitely be interesting, but would not produce something I could call a 3d M-set.

That was what I had in mind - something like the folds, which are two-to-one, conditional reflections. For me, it doesn't matter much that they are not completely conformal and have local symmetries - on many systems you are not able to see this. I also wonder, if it would be possible to construct something asymptotically conformal, where the inner transformations themselves were not conformal, but where later iterations might pull in 'the right direction', and make the system converge towards something conformal?

[s31415]

For me, it doesn't matter much that they are not completely conformal and have local symmetries - on many systems you are not able to see this.

It is definitely easy to see. Take the 2-dimensional case. The Mandelbrot-like patterns have local 180° rotation symmetry, while the ducks-like patterns have local mirror symmetries. The resulting patterns are completely different. See for instance these two sets of dense fractals:
http://algorithmic-worlds.net/expo/expo.php?Collection=Ducks
http://algorithmic-worlds.net/expo/expo.php?Collection=Dense+Julia
The only case in which they yield similar patterns is when Mandelbrot-like patterns happen to have mirror symmetries, like for instance in this image:
http://algorithmic-worlds.net/expo/work.php?work=20110410-invj3

And actually, my previous message was slightly incorrect. The squaring operation on the 2-sphere is not fully conformal either. It fails to be so at 0 and infinity.

About the "asymptotic conformal" idea, I am not sure I really get it... If you use some non-conformal iterations, your pattern will be stretched irremediably. And we really need a 2 to 1 or many to 1 map, which a priori cannot be a slight deformation of a conformal map...

[Syntopia]

It is definitely easy to see. Take the 2-dimensional case. The Mandelbrot-like patterns have local 180° rotation symmetry, while the ducks-like patterns have local mirror symmetries. The resulting patterns are completely different. See for instance these two sets of dense fractals:
http://algorithmic-worlds.net/expo/expo.php?Collection=Ducks
http://algorithmic-worlds.net/expo/expo.php?Collection=Dense+Julia
The only case in which they yield similar patterns is when Mandelbrot-like patterns happen to have mirror symmetries, like for instance in this image:
http://algorithmic-worlds.net/expo/work.php?work=20110410-invj3

I just meant that when you combing the reflections with rotations or inversions, they are not visually obvious anymore - for instance, if I look at:
http://www.fractalforums.com/index.php?action=gallery;sa=view;id=12332
I dont see the mirrors - only repeating structure.

About the "asymptotic conformal" idea, I am not sure I really get it... If you use some non-conformal iterations, your pattern will be stretched irremediably. And we really need a 2 to 1 or many to 1 map, which a priori cannot be a slight deformation of a conformal map...

It is just a loose thought. Since you may combine multiple non-conformal transformations into a single conformal transformation (for instance scaling each axis individially is three non-conformal transformations, but the combination is conformal), you might construct a system, which uses different transformations at each iteration, but doing it in a way, such the shearing/tearing would not accumulate, but instead be counteracted by later iterations. A way of averaging out the non-conformality, or making a series a transformations that converges towards something conformal.

Are you sure non-conformal stretching is irremidable? You might be right, but it is not obvious to me.

[mfg]

Your renders are extraordinary! What you will do with the real MacKay will surely be fantastic!

The 'universal' property is referring to 'small copies of M in M' in McMullen's article. Indeed, the term 'universal' has been used with several other meanings, in particular that higher order polynomials resemble polynomials of degree two when restricted to a suitable region. Fracmonk referred to 'repeated fractal shapes'. Sometimes, this property is confused with self-similarity. Let me quote Adrien Douady [A. Douady, Julia sets and the Mandelbrot set (Springer-Verlag, 1986)]:

“Julia sets are among the most beautiful fractals. Most of them are self similar: if you look at the boundary of a given 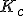with a microscope, what you see does not depend essentially upon where you look, nor on the magnifying power of the microscope. In contrast, the Mandelbrot set does not possess this property of self-similarity: certainly M contains an infinite number of small copies of itself, so that wherever you look in the boundary of M with a microscope, you will see some small copies of M. But these copies of M are embbeded in a network of filaments whose aspect depends very much on where you are looking. Moreover ...”

So the boundary of the confined set under quadratic iteration with complex numbers starting with 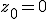produces an infinite number of small copies of itself.

Where and how these copies are produced is a more intricate matter. Which conditions are required for these copies to exist is also a very delicate issue. Whether, for example, angle preserving transformations (conformal mappings) or field conditions over hyper complex numbers are required. I am thinking on your various assertions ...

So the generalization  of the self copies property to three dimensions is:

The boundary of a 3D confined set starting with 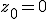should reproduce an infinite number of small 3D copies of itself.

Do you agree?

[s31415]

I just meant that when you combing the reflections with rotations or inversions, they are not visually obvious anymore - for instance, if I look at:
http://www.fractalforums.com/index.php?action=gallery;sa=view;id=12332
I dont see the mirrors - only repeating structure.

When combined with inversion, the mirrors turn into spheres, and indeed are more difficult to spot... Still I think I can in some places in this picture... anyway as I mentioned in the previous mail, my statement was not quite correct, as even the transformation used to construct the M-set is not conformal everywhere. So we probably just want to find new many to 1 "almost conformal" transformations in 3d. Ideally, they would need to fail to be conformal only at discrete points.

Are you sure non-conformal stretching is irremidable? You might be right, but it is not obvious to me.

That's only an intuition. To get a fractal, the orbits should get more and more entangled when you iterate the map. The map that would "undo" a stretch that had occured in an early iteration would have to be awfully complicated, if it exists at all.

The boundary of a 3D confined set starting with  should reproduce an infinite number of small 3D copies of itself.

This could be taken as a criterion, indeed. Although it is not clear what you mean by "copies". In the article, "copies" are images of the M-set under holomorphic maps. If you just allow any continuous map, then you can map the boundary of the M-set to a circle or to any closed curve.

[jehovajah]

Recognising the holy grail will not be easy.

The Mandelbrot set is described as the mapping of circles under the transform z^2+c. These circles are circular rings around the origin in the complex plane. In general in the plane circles map to circles scaled and pushed about all over the plane. This is fundamentally why the Mandelbrot image repeats at all scales and in all directions. This has been described as a conformal mapping besides which is another way of saying the form repeats at all scales and in all directions.

We know the world is a weird and wonderful place, but in fact it is pretty normal compared to the plane! We however get schooled into thinking the plane is normal. In space we might watch the whirling spinning motion of a butterfly with some delight, it's motions in space being generally trochoids or roulettes. We might mistakenly classify them as parabolic or elliptic or even hyperbolic, all of which derive from the plane analysis of such 3d motions.
Therefore we expect and comprehend the beautiful aerobatics of a butterfly, but tracing it on a plane leads to ugly kinks and loops.

In general, we know that a 3d description is going to be more awkward, more prone to misunderstanding, less aesthetically pleasing than a 2d one. Although the transform in 2d takes any functional relationship, producing many fractal images, the conic section functions generally produce Mandelbrot type images.

When we move into 3d space the general set of trochoids becomes weird and wonderful. The corresponding analogy in 3 d space would be conformal mappings of spheres, but now they can be pushed or placed along wonderful trochoid trajectories, and they hang like a mist obscuring the view of the mountain peaks.

I do not think you can expect to see much without some way of filtering out the fog of tiny spherical droplets that surround.
What filters might one use? Apart from texture and surface filters it may be necessary to filter out those trajectories that are least like Mandelbrot 2d trajectories. I have no clue how to do this, but Matt Benesi has the expertise, and is currently using quaternion maps to do this.
http://www.skytopia.com/project/fractal/2mandelbulb.html#epilogue

The spherical drops have been seen by twinbee

[jehovajah]

One of the fundamental aspects of the Mandelbulb is that it is made up of spheres at different scales and disposed along trochoidal trajectories. This immediately means that the mandelbulb based on the sphere will be " infinitely" scaleable, an exact counterpart to the Mandelbrot.. Thus what is important is the surface colouring and contrast algorithms.

For something as subtle and varied as 3d space, I think the most subtle, and wide spectrum colouring algorithms will be necessary.

The isolation of form from this  field effect coloration will key into our interpretation processes at our deepest levels, but the bare form should be discoverable by the tightest of constraints on the coefficients, by choosing scalars for the y and z orientation coefficients I can strip the outcome down to whatever skinny or fat form I care to explore.