Among the scalars of unity the
primes play an interesting part. They really show that scaling as an operation: that is proportioning and ratioing can be sorted into independent scaling "seeds". So for example if unity is fundamantal then the next fundamental scalar is 2. This means that i can reduce or scale down certan ratios to a "seed" of 2.
Three is the next fundamental scalar because of course bundling in 2" will not capture 3 and similarly i can scale down certain ratios to a seed of 3. It becomes apparrent that the prme numbers are interellated by scaling as 3 can be scaled to 6 as can 2. Systematically going through the scalars to find how scaling works, that is an analysis of scaling reveals these "seed" numbers which are all scalars of unity but which unlike unity scale to pick out only certain numbers.
To a geometer this evidence of a kind of mesh, ameshing together of these seed number scales explains the fundamental nature of the unity, and describes in a way how all thingsdeveloped from unity. Of course unity had to be male!
This mesh was related to an actual sieve mesh by Euclid, and a spatial arrangement was used to describe this curious mesh arrangement, by relating it to finding the area by multiplying the side lengths of rectangles. This mesh partitioned rectangles into equivalence classes, and related directly to proportioning as well as to bundling or packing.
So for a while Pythagoras had a nice little thing going there with is theory of unity being fundamental, and worthy of study for that sake alone! Theodorus, shut up!!
What Theodorus showed was that primes or proto arithmetical objects, with the pythagorean theorem did not produce scalars of unity, or eve scalarsof proto aritmetical objects, so even the prot objects were not "proto" in that sense.
My guess is that Theodorus got the short end of the stick if not the sharp end of a dagger! That is how important it was. It took Eudoxus to restore equanimity and maintain"unity" by explaining the arithmoi as scalars the solution of all proportioning, and that these irrational numbers could be proportioned and scaled among themselves. Thus the arithmoi maintained their foundational and "creative" status status to this day. Some like to stand in awe of number in the style of Pythagoras even now.
So geometric measure and the right triangle "rule" with the aid of the arithmoi are seen to give birth to a whole new set of ratios,never before conceived, but children of tha arithmoi.
When negative numbers were introduced, as debt mainly, their geometric nature demanded an origin, which is why the Indians were far advanced in their use and consequences and their sign rules and also their consequence of √-1.
For me this leads to the measure being the fundamental arithmoi: arithmetic and geometric object and as theodorus showed, the unit circle and sphere being the fundamental proportion or scalar, and consequently the mesh of prime measures being spiral in nature.
Of course if a circle or sphere is a proportion this makes an measure necessarily a vector, that is having magnitude and direction, and square rooting a geometrical operation or algorithm. In fact it reveals that all operations are geometrical operations not counting ones. Therefore, and it took a long while to realise this we need to define all operations geometrically and rigorusly.
Descartes began to do this in his Geometry and continued to do so all his geometrical career. Thus Arithmetic was sidelined as a practical case of a more general geometric construction, with a restricted set of operators. However mathematicians clung on to their familiar arithmoi with a religious fervour insisting that all True mathematikos should make them supreme, including their field properties.
Over time algebraic analysis and categorisation has lead to a downgrading of the integroi but has maintained a commensurate high regard for the field properties. However i think we have to find a geoemetrical definition of the field properties or behaviours if they are to survive as algebraic analytical fundamentals.
Thus Bombelli using a set square vector with neusis has in a practical and applicable form all the elements so far alluded to in this story": the integral scales on both perpendicular/ orthogonal sides of the set square the incommensurable third side, the trigonometry, and the neusis, and the √-1.
From this geometrical start, polynomials of all sorts flow, and their inherent nature is that of a vector algebra of geometry. Polynomials are vectors and an algebra of vectors and a training in vector math that was of course not understood in this way, because "number" a translation of arithmoi was in many peoples head, along with the pythagorean and archimedian doctrine.
It was not until Descartes that the doctrine or matheis substantially changed, but the √-1 he could not conceive of. He did not have the "intelligence" of Bombelli, who in his travels may have gleaned that the indians had done work on this, and trusted to his instinct or intuition or intrguing discoveries and meditations. In any case Descartes had little time for it and derided it elegantly. His name for them stuck and in fact inspired an interest in them that lead Euler to find his remarkable equation and gauss to prove the fundamental theorem of polynomials, which i now regard as a fundamental theorem of vector algebra.
You have all heard of

And of course many here know

Which Euler arrived at because of his love of power series polynomials, which we would call infinite vectors today. Just as Einstein showed through polynomial transformations that the "rest" motion of a body is not zero but a scalar of value m*c*c
Euler showed that the infinite vector

has a form directly related to the trig functions on the unit circle, which describe a continuous series of right angled triangle measures with hypotenuse of unity. These right angled triangle measures relate directly by symmetry to Bombelli's set square and is the reason why i define the set squares as vector models
Formally and fortunately convergent Eulers equation is the definition of unity for all planar vectors. it therefore must be a basis for all planar vectors.
I will have to check but i think this is what Hamilton established in his seminal work on couples.
Hamilton therefore looked for a generalisation to 3d and at the same time a change in the doctrine of numbers up until then, for he could see that the doctrine of imaginaries was a better or more useful mathesis for algebraic geometry than those of former times. He had a hard time but couples at least maintaned the field properties.
He gave up after ten years of looking for a solution in 3 variables, and looked at four variables. By this i mean he attempted to reduce infinite series to an algebraic system using the trig function series (Fourrier analysis) , the x polynomial series without success because he was seeking a scalr value for i*j to make sense in completeness terms. Thus when he eventually abandoned the attempt and moved to 4 variables he had substantially done al the work, and was able to show that an infinite series of quaternions converged to a quaternion.
So using a polynomial vector Hamilton established a general vector math after Cotes, Euler, Graves in the plane and another one After Euler with
4 variables which he took to represent a vector with a scalar time component.
Thus the 3d vector is given by
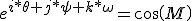+L sin(M))
"The quantity
/sqrt (\theta^2 +\psi^2 + \omega^2) satisfies L^2 = -1)
(check it
for yourself). And you can go back to the infinite series to see that
exp Lx = cos x + L sin x, whenever L^2 = -1 and x is real. So let
)
, so

Then
 = exp a *(cos M + L sin M).)
"
Hamilton realises that to make sense of these values they have to be applied to arc lengths on the surface of the unit sphere, thus establishing a use for a
radian measure.


















