|
|
|
Syntopia
|
 |
« Reply #31 on: May 03, 2011, 10:06:49 AM » |
|
Wait a minute... look at this:
z=abs(1/z)+c
Well, it is the same formula: 1/z = 1/(x+yi) = (x-yi)/(x^2+y^2) = conj(z)/m, where m = x^2+y^2
so abs(1/z) = abs(conj(z))/m = abs(z)/m
So we are dealing with kind of an "absoluted negative power mandelbrot" <- good name!  There is already an 'abs' version of the power-2 Mandelbrot - the Burning Ship Fractal. So your fractal is actually a power -1 burning ship :-) By the way, I think the similarity to the Ducks fractal is mainly due to the folding (abs) operator. You will find similiar motifes using folding (abs), scaling, and rotation - and many of these are also found in the 3D KIFS of Platonic Solids, which also use such operations. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #32 on: May 03, 2011, 01:40:09 PM » |
|
There is already an 'abs' version of the power-2 Mandelbrot - the Burning Ship Fractal.
So your fractal is actually a power -1 burning ship :-)
I logged in to post exactly that but you did it for me!  Thanks for additional info... I know a little about KIFS, very interesting stuff. @Kraftwerk: Thanks, but keep in mind is quite different from others M3D formulas, you must use julia mode with negative values, bailout values between 1 and 3, and maybe do some cuts with some Julias, or zooming out because this are space-filling patterns. Also I found difficult to navigate, do it with "fixed zoom and steps" mode. Have fun! 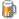 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #33 on: May 03, 2011, 02:12:40 PM » |
|
I added some rotation for this (a quick render, sorry, I'm on a netbook!  ) It seems there's a cold front coming  (Is not a post-work!  ) |
|
|
|
 Logged
Logged
|
|
|
|
|
KRAFTWERK
|
 |
« Reply #34 on: May 03, 2011, 04:53:27 PM » |
|
Yes, looks like rain...  Ill keep your tips in mind Kali, Thanks! 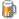 |
|
|
|
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #35 on: May 03, 2011, 10:02:44 PM » |
|
@Jesse: tried your formula and works better than the custom I made and also faster, nice!
Still think about r parameter... I mean m<r part, and not using m<1...
Just this way:
if m<r
---
---
else
---
---
endif
Did you try somthing like this and it looks such the same as Mandelbox with all julias?
Asking this cause I get different stuff in 2D
The one you mentioned looks not that much like a common mandelbox, i will try it in the next days if i find the time. Just looked at the origin mandelbox spherefolding because you could use the analytic DE method, what gives a 4x speedup. But i guess the 1/z thingy has no such easy analytic method, it was just a thought to forget... |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #36 on: May 04, 2011, 12:32:57 AM » |
|
Well, I think I missed something, or this is totally unknown? (At least I did a google search on this and didn't find it): The inside of the regular "burning ship" fractal is actually a collection of this kind of patterns! I used exponential smoothing for coloring, as most of my 2D images, look:  Zoom:  This is a Julia sample:  Perhaps nobody used before this coloring method with the Ship? Or maybe didn't find it interesting?  Who knows... please let me know if this is already known, I'm only recently become a "fractalist" after all  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
cKleinhuis
|
 |
« Reply #37 on: May 04, 2011, 12:49:47 AM » |
|
the glynn julia shapes in the last image are fantastic!
*just a side note, continue discussing*
|
|
|
|
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
Kali
|
 |
« Reply #38 on: May 04, 2011, 05:05:59 AM » |
|
(Thanks Chris) This is a variation with a bigger set of patterns... z=abs(z^2)+c (instead of abs(z)^2+c): The first are in Google Earth mode: <-    Nice structures:  Emerging patterns:  Gold patterns:  Actually burning:   And a beatiful Julia:  I think I should open a new thread on this! |
|
|
|
« Last Edit: May 04, 2011, 05:08:47 AM by Kali »
|
 Logged
Logged
|
|
|
|
|
s31415
|
 |
« Reply #39 on: May 04, 2011, 09:15:12 AM » |
|
This is not extremely surprising. If you take a random conformal transformation together with a folding operation, you are very likely to get some region of parameter space looking like this and producing standard Ducky-Thalis patterns. What I found special with Ducks is that some of the "Julia sets" are infinitely extended. This seems to be the case as well with the Kaliset formula you first proposed.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
xenodreambuie
|
 |
« Reply #40 on: May 04, 2011, 10:51:31 AM » |
|
I'm glad to see more variations on this these patterns, and disappointed that in general inverse methods don't seem to produce clean attractors.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #41 on: May 04, 2011, 11:43:23 AM » |
|
This is not extremely surprising. If you take a random conformal transformation together with a folding operation, you are very likely to get some region of parameter space looking like this and producing standard Ducky-Thalis patterns. What I found special with Ducks is that some of the "Julia sets" are infinitely extended. This seems to be the case as well with the Kaliset formula you first proposed.
My surprise is because this is supposed to be a well known fractal and I didn't find any references on this patterns appearing inside of it. I suspected this just because of what you are telling (I learned it from you on the other thread  ) By the way, maybe you can answer this: why the "Kaliset" formula is not a map of this patterns in "mandelbrot" mode? |
|
|
|
« Last Edit: May 04, 2011, 11:46:31 AM by Kali »
|
 Logged
Logged
|
|
|
|
lkmitch
Fractal Lover
 
Posts: 238
|
 |
« Reply #42 on: May 04, 2011, 06:06:12 PM » |
|
I tried a version of the kaliset and found an Apollonian packing. In my formula, I used the simple one-statement loop:
z=1/abs(z)+c
and I found this image in a Julia version.
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #43 on: May 04, 2011, 07:00:32 PM » |
|
@lkmitch: Very nice, what julia values? (if you saved them  ) I was exploring the burning ship fractal a moment ago (I will not open a new thread because it's actually related to my formula), and I think this are minibrot-like structures among the patterns ("miniships"  ) |
|
|
« Last Edit: May 04, 2011, 07:22:30 PM by Kali »
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #44 on: May 04, 2011, 07:35:39 PM » |
|
I raised the iterations, and they are, indeed... also I raised more the iterations and color density, and there are patterns inside the miniship that is among the patterns of the main ship. So there must be miniships inside the patterns of the miniship that is among the patterns of the main ship... ... and also there must be patterns that... Ok enough!  |
|
|
|
 Logged
Logged
|
|
|
|
|


















