stardust4ever
Fractal Bachius

Posts: 513
|
 |
« Reply #255 on: August 31, 2016, 03:50:24 AM » |
|
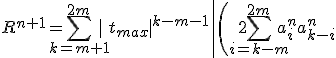%20+\left%20(%20(a_{\frac{k}{2}}^n)^2%20\:if\:k\:even\right%20)%20\right%20|%20+%202%20R^n\left%20[%20|z_n|%20+%20\sum_{i=1}^{m}%20|a_i^n|%20|t_{max}|^i%20\right%20]%20+%20(R^n)^2%20|t_{max}|^{m+1}) While I have a very advanced knowledge of complex math, infinite series and such are beyond me. This is why I flunked advanced Calculus! Carry on...  |
|
|
|
« Last Edit: August 31, 2016, 04:17:50 AM by stardust4ever »
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #256 on: August 31, 2016, 11:04:47 AM » |
|
<Quoted Image Removed>
just curious, earlier it was written as |tmaxn|, but according to this it seems to be |tmax|n. should these be equivalent or should it be one or the other?
also,
<Quoted Image Removed>
this seems weird to me... for instance at m=3 and k=4, this seems to give 2(a1a3 + a2a2 + a3a1 + a4a0 + a5a-1 + a6a-2). should that 2m instead be m ?
Oops! it is a copy past mistake!   It should be :  I'll make the corrections to the previous post. In the other hand we always have : |z n| = |z| n |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kalles Fraktaler
|
 |
« Reply #257 on: August 31, 2016, 12:28:46 PM » |
|
added my own method of recursive glitch solving to the code, hopefully it is useful to see a simple implementation without multithreading optimisations getting in the way of understanding.
claude, I think your render is not correct. You may have encountered the distortions near the edges as was showed by knighty. I attached about the same location rendered in KF that is able to skip 3407 iterations with 126 terms. Even with 1000 terms KF is not able to skip more than 3509 terms. Sorry to spoil your progress...  |
|
|
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #258 on: August 31, 2016, 12:43:22 PM » |
|
indeed, i get the same render as kalles skips 3544 iterations this would certainly be the right number of iters to skip though if possible, as the min iter i get for this image is 3554.  |
|
|
|
« Last Edit: August 31, 2016, 12:53:02 PM by quaz0r »
|
 Logged
Logged
|
|
|
|
|
Kalles Fraktaler
|
 |
« Reply #259 on: August 31, 2016, 12:59:53 PM » |
|
indeed, i get the same render as kalles this would certainly be the right number of iters to skip though if possible, as the min iter i get for this image is 3554.  I think 3544 is too much near the edges. I assume this is because of limited precision. I guess it would be possible to skip all the 3554 only if the SA is calculated with the same precision as the reference of e42. |
|
|
|
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #260 on: August 31, 2016, 01:13:38 PM » |
|
if possible  I assume this is because of limited precision. I guess it would be possible to skip all the 3554 only if the SA is calculated with the same precision as the reference of e42. since the series approximates the delta instead of the whole value, i think the number of terms in the series is the only limiting factor? with infinite terms i suppose you could get right up to within the min iter... though maybe as you get close the delta would indeed require more precision. could that theoretically be a limitation on analyzing the coefficients only versus the old way of actually testing points? i think the coefficient analysis should give a theoretically proper stopping point, though perhaps precision loss could potentially occur prior to this point? ie this is what the automatic perturbation glitch detection does, detects catastrophic loss of precision, but i have never heard of anyone implementing such a check for the series approximation. would it go on to be detected by the perturbation glitch detection? or possibly get through undetected, which would result in went-too-far-with-SA style incorrectness. another thought: if SA precision loss was indeed an issue to be accounted for, and you added a check for it, perhaps this information could then also be used to provide feedback about how many series terms were actually useful up to the point where you had to bail due to precision loss? |
|
|
|
« Last Edit: August 31, 2016, 01:54:55 PM by quaz0r »
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #261 on: August 31, 2016, 02:29:54 PM » |
|
claude, I think your render is not correct. ... Sorry to spoil your progress...  Well spotted! Oh dear  EDIT EDIT: I found the problem - my code was using a too-small tmax value (half the imaginary diameter of the image). Increasing the tmax by a factor of 4 gives a correct render it seems! This skips 3294 iterations with 16 terms, using knighty's first version of the R calculation (will see how the updated R iteration affects things next). |
|
|
« Last Edit: August 31, 2016, 04:23:36 PM by claude, Reason: all is not lost »
|
 Logged
Logged
|
|
|
|
|
Kalles Fraktaler
|
 |
« Reply #262 on: August 31, 2016, 04:05:41 PM » |
|
 since the series approximates the delta instead of the whole value, i think the number of terms in the series is the only limiting factor? with infinite terms i suppose you could get right up to within the min iter... though maybe as you get close the delta would indeed require more precision. could that theoretically be a limitation on analyzing the coefficients only versus the old way of actually testing points? i think the coefficient analysis should give a theoretically proper stopping point, though perhaps precision loss could potentially occur prior to this point? ie this is what the automatic perturbation glitch detection does, detects catastrophic loss of precision, but i have never heard of anyone implementing such a check for the series approximation. would it go on to be detected by the perturbation glitch detection? or possibly get through undetected, which would result in went-too-far-with-SA style incorrectness. another thought: if SA precision loss was indeed an issue to be accounted for, and you added a check for it, perhaps this information could then also be used to provide feedback about how many series terms were actually useful up to the point where you had to bail due to precision loss? I tried with 10,000 terms, which took more than an hour to calculate and resulted in 3530 skipped iterations  |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #263 on: August 31, 2016, 06:51:39 PM » |
|
The value of tmax is critical. It must be the distance from the reference to the farthest corner of the rendered area. If less, it will go too far in skipping.
In the other side the value of dt is much less critical.
In this particular location, with 16 terms, the test gives exactly the maximum iteration skip possible: 3298. With 32 terms, the max possible skip is 3380 while the test still gives 3298... strange! maybe it is the lower bound of the derivative that is preventing it to go further.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kalles Fraktaler
|
 |
« Reply #264 on: August 31, 2016, 11:53:34 PM » |
|
Even though you are able to achieve a theoretically accurate way to find the highest amount of skippable iterations in a radius of the most farther point from the reference, which is a good improvement, can you be sure that you will capture totally entrapped areas within this radius where only a lower amount of skippable iterations is possible?
|
|
|
|
|
 Logged
Logged
|
|
|
|
hapf
Fractal Lover
 
Posts: 219
|
 |
« Reply #265 on: September 01, 2016, 09:50:20 AM » |
|
Even though you are able to achieve a theoretically accurate way to find the highest amount of skippable iterations in a radius of the most farther point from the reference, which is a good improvement, can you be sure that you will capture totally entrapped areas within this radius where only a lower amount of skippable iterations is possible?
I guess not because we are talking about fractals.  |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #266 on: September 01, 2016, 04:24:54 PM » |
|
Even though you are able to achieve a theoretically accurate way to find the highest amount of skippable iterations in a radius of the most farther point from the reference, which is a good improvement, can you be sure that you will capture totally entrapped areas within this radius where only a lower amount of skippable iterations is possible?
I'm not sure I understand your question. The whole thing is about having a guaranteed number of skipped iterations as to not have any deformation and that, over the whole rendered area. This guaranteed number will be always less or equal to the max skippable iteration number that is possible -without getting any deformation-. That said, there is still some work to do in order to finish the test part. |
|
|
|
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #267 on: September 02, 2016, 03:43:30 AM » |
|
can you be sure that you will capture totally entrapped areas within this radius where only a lower amount of skippable iterations is possible? i believe this is exactly the point of interval arithmetic, to compute bounds that you can be sure will hold true over the given interval. I'm not sure I understand your question. i imagine those of us who are not math professors are likely unfamiliar with interval arithmetic. also i think the experience thus far of testing against points and hoping for the best is tainting future optimism that there could actually be a better way  |
|
|
|
« Last Edit: September 02, 2016, 04:11:33 AM by quaz0r »
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #268 on: September 02, 2016, 09:34:00 AM » |
|
 im still not sure about this part.. when k=2m, for instance say m=3 and k=6, we get k-m=3 and  =2. ive never seen 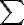 start higher and go lower. was that your intention? |
|
|
|
|
 Logged
Logged
|
|
|
|
stardust4ever
Fractal Bachius

Posts: 513
|
 |
« Reply #269 on: September 02, 2016, 09:39:14 AM » |
|
i imagine those of us who are not math professors are likely unfamiliar with interval arithmetic.  This!  |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















