Buddha's Jewel: a special subset of the Buddhabrot, symmetrical about both axis!

[Chris Thomasson]

dude, the last pic is marvellous!

this looks so 3d ish

I have to second that observation!

:^)

[Chris Thomasson]

FWIW, this post inspired me to create my vary first BuddhaBrot:




:^D

[cKleinhuis]

so, this is a classic buddhabrot or using billtavis technique ?!  

gosh, those buddhabrots are full of interesting stuff and your coloring is amazing ... looks like this year is standing under the light of the BUDDHA


i see you posted it in the gallery, i edited your post and included the link to the entry  
http://www.fractalforums.com/index.php?action=gallery;sa=view;id=17279

[cKleinhuis]

so, regarding buddhabrots in general,
i am a bit disappointed that you dudes do not render different formulas (and hybrids) as buddhabrots

especially using the fine adjustments introduced by billtavis a chest has opened up to bring buddhabrots to a whole new life ... who is in for making a user interface for a nice buddhabrot renderer !?    

 

[3dickulus]

stunning images! 

I've looked at ker2x's buddhaGenerator, to be more specific the one on github by Emilio Del Tessandoro and managed to get some interesting images but none like those presented here.

[Sockratease]

so, regarding buddhabrots in general,
i am a bit disappointed that you dudes do not render different formulas (and hybrids) as buddhabrots
...

I wonder if anybody ever tried folding a Buddhabrot into a Buddhabox or a Buddhabulb?

It's based on the same formula as the Madelbox/bulb  (z=z^2 + c), so unless I am missing something  (and I do tend to miss things when making these suggestions!) it should be possible   

Very nice images!  Got me looking through my old software to see what Buddhabrot Generators I may have already...

[kram1032]

so, regarding buddhabrots in general,
i am a bit disappointed that you dudes do not render different formulas (and hybrids) as buddhabrots

That's what I've been doing for a while here
http://kram1032.deviantart.com/gallery/8114987/Fractals
But I haven't done any new ones in quite some while. I think I need to write a new renderer at some point. The one I used - modified from an already working one I found running in Processing way back when - is really slow.

Really nice pictures in this thread, especially the last couple since the one that, I must third, looks almost 3Dish.

[cKleinhuis]

i once did a hybrid buddhabrot generator but cant find any sources, the buddhabrots are existant for any escape time formula, it is just a way to visualise the iteration process, yes, the buddhabox or the buddhaship (lols) they are all existant, the time seems ripe now for them to come out to the surface

[Chris Thomasson]

so, this is a classic buddhabrot or using billtavis technique ?!  

gosh, those buddhabrots are full of interesting stuff and your coloring is amazing ... looks like this year is standing under the light of the BUDDHA


i see you posted it in the gallery, i edited your post and included the link to the entry  
http://www.fractalforums.com/index.php?action=gallery;sa=view;id=17279

This is basically a classic Buddhabrot. I am not using billtavis' technique, yet...  ;^)

I actually iterated all of the points in the plane here and for each iteration I found the corresponding pixel and added some color's.

Also, I when a pixel escapes, I added some more color to the pixel. One more thing, I did not use any orbit traps.

[Chris Thomasson]

FWIW, here is a zoom on the last rendering of the Buddhabrot I created: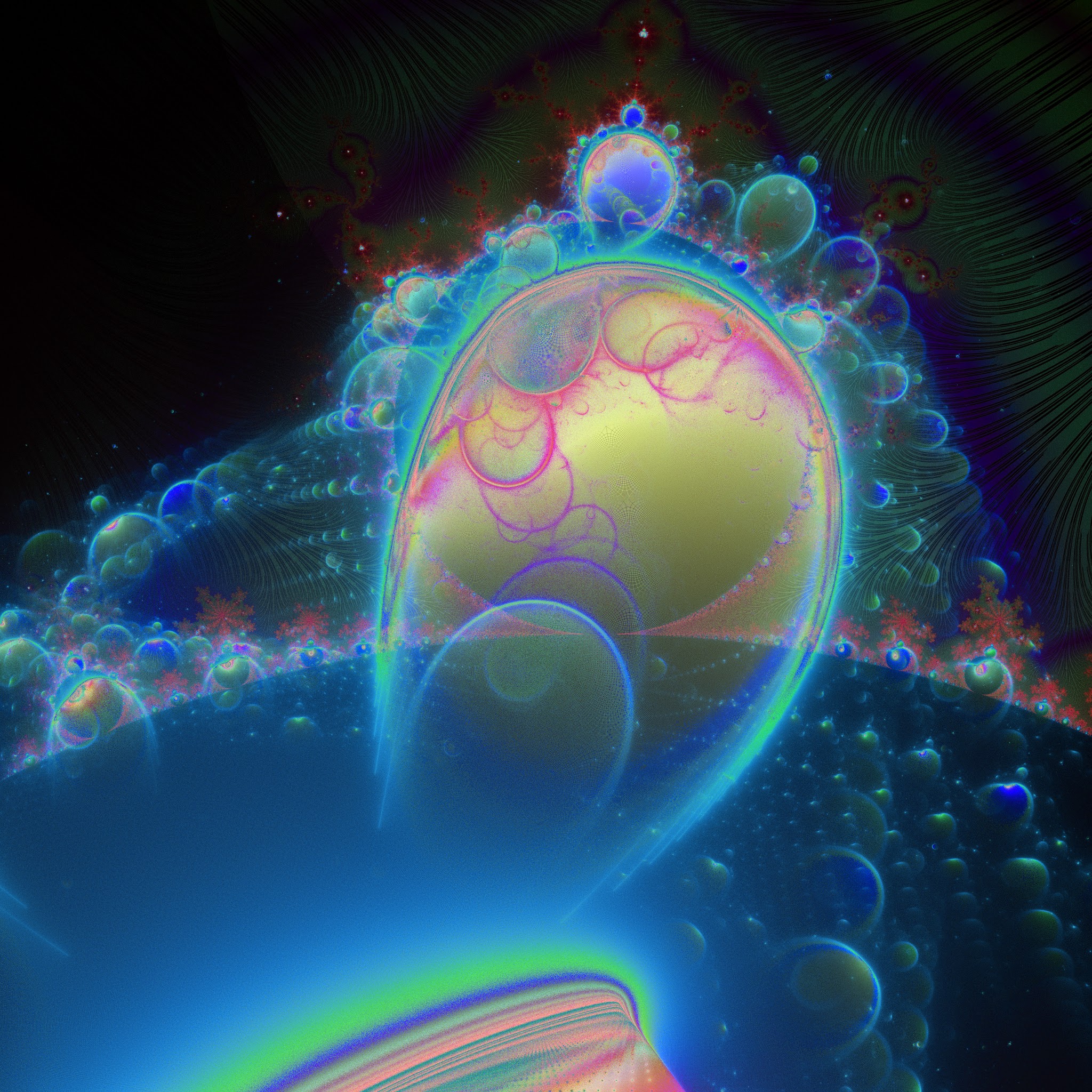



It seems I lost a bit of information here. It has be due to the fact that the zoom basically cropped some of the iterations.

Humm...

[claude]

This is basically a classic Buddhabrot. I am not using billtavis' technique, yet...  ;^)

I actually iterated all of the points in the plane here and for each iteration I found the corresponding pixel and added some color's.

Also, I when a pixel escapes, I added some more color to the pixel. One more thing, I did not use any orbit traps.

As I understand it, the classic Buddhabrot plots iterates only of points that escape - points that don't escape are not plotted.  The anti-Buddhabrot plots iterates only of points that don't escape - points that escape aren't plotted.  Looks like you plotted both with different weights, giving some kind of hybrid "dark matter" Buddhbrot?

I wrote a post about the Ultimate anti-Buddhabrot, which plots only the limit-attractors of points that don't escape:  http://mathr.co.uk/blog/2013-12-30_ultimate_anti-buddhabrot.html  I did some other experiments around that time (late 2013) using something very similar to billtavis' technique, no pics online at the moment though (and will take me some time to trawl my hard drive to find them to upload, might instead take a photo on Sunday of the print hanging on my parents' wall...).

My technique was to trace (using Newton's method) external rays at pre-periodic external angles inwards towards the Mandelbrot set, stopping when the iteration count reaches a certain limit - then plotting all the iterates.  Pre-periodic angles land at Misiurewicz points, and for some reason still unknown to me they are much quicker to trace than periodic angles which land at cusps and bond points.  The other difference from billtavis' method was the colouring - I plotted iterates in colours corresponding to the external angle (in HSV colour space, the angle would be the hue).

If you don't split the rays into periodic and pre-periodic subsets, the pre-periodic part totally dominates - "most" angles are pre-periodic, and in fact any binary floating point representation will be pre-periodic (apart from the period 1 ray at angle 0).

[ker2x]

Some old attempts at 3D buddhabrot

<a href="http://www.youtube.com/v/iPp781NtSFQ&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/iPp781NtSFQ&rel=1&fs=1&hd=1</a>

[cKleinhuis]

so, who wants to try a buddhabox ?

[Chris Thomasson]

Some old attempts at 3D buddhabrot

Well, if were going to do a 3d Buddhabrot, I would find every corresponding voxel during iteration of the center slice (z-axis of zero) of the Mandelbulb, and start adding color. It is basically the same as 2d, except you use an extra dimension when mapping a point Z to its pixel.

Humm...

[Chris Thomasson]

Well, if were going to do a 3d Buddhabrot, I would find every corresponding voxel during iteration of the center slice (z-axis of zero) of the Mandelbulb, and start adding color. It is basically the same as 2d, except you use an extra dimension when mapping a point Z to its pixel.

Humm...

Actually, one would need to make sure that the z-axis goes above, or lower than zero during iteration. Now that I think about it, the center slice at z-axis 0 might not ever change from zero. Keep in mind that I am not completely skilled in the art of Mandelbulb iterations.

;^o