|
kram1032
|
 |
« Reply #60 on: December 10, 2009, 12:23:48 AM » |
|
congratulation, you found the 3D Mandel-heart  |
|
|
|
|
Logged
|
|
|
|
|
cbuchner1
|
|
« Reply #61 on: December 10, 2009, 12:49:17 AM » |
|
congratulation, you found the 3D Mandel-heart I am going to post more images in the Mandelbulb Renders forum - in particular what happens when one points the pole vector in some other direction. |
|
|
|
|
Logged
|
|
|
|
|
cbuchner1
|
|
« Reply #62 on: December 11, 2009, 03:04:29 AM » |
|
My wild guess is that it "lathes" the Mandelbrot set around its axis...
I am so glad that you are wrong. How embarassing. You were right. The Mandelbrot is lathed around its axis. I should never again claim that someone is wrong so qickly. I must have made a severe mistake in the trigonometric code that performed the rotations. After I implemented a non-trigonometric version (based on some results I got with the help of a Mathematica trial version) I get this. Wonderfully lathed indeed.  Now i need to investigate what kind of malfunction I have in my approach to rotation because indeed it gave nicer results  |
|
|
|
« Last Edit: December 11, 2009, 03:06:08 AM by cbuchner1 »
|
Logged
|
|
|
|
|
Paolo Bonzini
Guest
|
|
« Reply #63 on: December 11, 2009, 12:42:04 PM » |
|
My wild guess is that it "lathes" the Mandelbrot set around its axis...
I am so glad that you are wrong. How embarassing. You were right. LOL, no problem at all! Talk about serendipity. :-) |
|
|
|
|
Logged
|
|
|
|
|
BradC
|
|
« Reply #64 on: December 15, 2009, 02:39:21 AM » |
|
Here is the solution for the exponential function:
Awesome! I had Mathematica sum this in terms of x, y, z instead of r, theta, phi, and I got results that numerically match yours. I tested my results with 100k points where x, y, and z were randomly chosen between -4 and 4, and our answers always agreed to at least ~12 digits. In terms of x, y, z: }=\left(\frac{1}{2} e^{x-t y} \left(\cos (t x+y)+e^{2 t y} \cos (t x-y)\right),\frac{1}{2} e^{x-t y} \left(\sin (t x+y)-e^{2 t y} \sin (t x-y)\right),e^{\sqrt{x^2+y^2}} \sin (z)\right)) where  |
|
|
|
|
Logged
|
|
|
|
|
David Makin
|
|
« Reply #65 on: December 15, 2009, 03:12:30 AM » |
|
Here is the solution for the exponential function:
Awesome! I had Mathematica sum this in terms of x, y, z instead of r, theta, phi, and I got results that numerically match yours. I tested my results with 100k points where x, y, and z were randomly chosen between -4 and 4, and our answers always agreed to at least ~12 digits. In terms of x, y, z: where Most excellent ! log() anybody ? |
|
|
|
|
Logged
|
|
|
|
|
BradC
|
|
« Reply #66 on: December 15, 2009, 07:36:15 AM » |
|
Here's what I get for the natural log: =(a,b,c)) where  x+(y-1) y) \left((x-1) x+y^2+y\right)}{t}+\left(x^2+y^2\right)^2+z^4\right))  z-\sqrt{t} y,\sqrt{t} x+y z\right)+\text{atan2}\left(\sqrt{t} y+(x-1) z,\sqrt{t} x-y z\right)-\text{atan2}\left(-\sqrt{t} y-x z+z,\sqrt{t} x-y z\right)+\text{atan2}\left(\sqrt{t} y-x z+z,\sqrt{t} x+y z\right)\right)) ) ^2+y^2) I derived this by analogy with the series expansion for ln(z) about z=1, which is =\sum _{k=1}^{\infty } \frac{(-1)^{k-1} (z-1)^k}{k}) . For triplex numbers I did the following: o ) became ) . o Raising to power 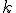 used the regular integer power formula. o For multiplying by ^{k-1}}{k}) , I multiplied each component of the triplex by . o Sum each component of the triplex separately. o Feed the whole mess to Mathematica and have it simplify the result as much as possible. I tested these results by comparing a large number of random points within 1/4 unit of (1,0,0) to this triplex series truncated to 1000 terms. The results all matched to 16 digits. I only used sample points near (1,0,0) because this series has a limited radius of convergence. Using this formula, we get the following: =(\ln (|x|),0,0)) . ) is undefined, but =(0,0,0)) . This is analogous to =0) . =(1,0,0)) . Analogous to =1) . ) is 0 (it should be pi), but =(0,\pi ,0)) and =(0,-\pi ,0)) . This is similar-ish to =i \pi) . Unfortunately, for most triplex numbers, this log formula and the exp formulas above don't appear to be inverses of one another. |
|
|
|
« Last Edit: December 15, 2009, 07:42:42 AM by BradC »
|
Logged
|
|
|
|
|
bugman
|
|
« Reply #67 on: December 15, 2009, 07:52:32 PM » |
|
Here is the solution for the exponential function:
Awesome! I had Mathematica sum this in terms of x, y, z instead of r, theta, phi, and I got results that numerically match yours. I tested my results with 100k points where x, y, and z were randomly chosen between -4 and 4, and our answers always agreed to at least ~12 digits. In terms of x, y, z: where Good work BradC. I just tried to further simplify my formula and indeed it exactly reduces to your formula. I don't know why I didn't see this before. Here is the simplified formula using the notation from my original formula: |
|
|
« Last Edit: December 16, 2009, 07:03:58 AM by bugman »
|
Logged
|
|
|
|
|
BradC
|
|
« Reply #68 on: December 16, 2009, 02:23:53 AM » |
|
I've done some numerical experiments regarding a triplex^triplex power function... If we identify the complex number  with the triplex number ) , and if we define ^{(x,y,z)}=e^{(x,y,z) \ln (a,b,c)}) using the above series-based definitions of exp and ln, then the equation ^{(c,d,0)}=(a+i b)^{c+i d}) appears to hold for \text{ and }(c\neq 0\text{ or }d\neq 0)) . In other words, this triplex power operation is equivalent to the complex power operation almost everywhere, so it's basically a generalization of the complex power operation.  Note that since triplex multiplication is commutative, we don't have the same ambiguity when defining the power function that quaternions have (see http://www.fractalforums.com/theory/rasing-a-quaternion-to-a-quaternionic-power/). |
|
|
|
|
Logged
|
|
|
|
|
BradC
|
|
« Reply #69 on: December 16, 2009, 02:31:33 AM » |
|
A picture of the triplex exponential map:
|
|
|
|
Logged
|
|
|
|
|
cbuchner1
|
|
« Reply #70 on: December 16, 2009, 02:38:22 AM » |
|
A picture of the triplex exponential map:
Beautiful! |
|
|
|
|
Logged
|
|
|
|
|
kram1032
|
|
« Reply #71 on: December 16, 2009, 04:56:31 PM » |
|
very nice map which looks pretty much analogous |
|
|
|
|
Logged
|
|
|
|
|
bugman
|
|
« Reply #72 on: December 16, 2009, 06:24:37 PM » |
|
That is really interesting. I would like to examine your formulas when I have more time. I also found a formula for ln({x, y, z}} and sin({x, y, z}) but they were very long and I haven't had time to see if I could simplify them.
|
|
|
|
« Last Edit: December 16, 2009, 09:52:58 PM by bugman »
|
Logged
|
|
|
|
|
kram1032
|
|
« Reply #73 on: December 16, 2009, 07:33:36 PM » |
|
ln is the only thing that would be missing to have a nice formula for "true" exponentiation |
|
|
|
|
Logged
|
|
|
|
|
|
|
January 26, 2009, 07:12:10 PM
Secant Cosine
2D Art
Dilber MC Theme by HarzeM