|
jehovajah
|
 |
« Reply #165 on: March 22, 2014, 07:41:55 PM » |
|
Commentary A remarkble section giving insight into the mind developing the method of analysis and synthesis which is the subject of this book. The next section concentrates upon a number of philosophical and academic issues relating to mans perception of space and his relationship to it. Hermann gives a reason why this first volume is more philosophical, and why his plan of presentation was decided upon. But in these 2 translations he carefully reveals part of the process of deriving his label methods. The Muse plays a large role in the artists life. Most scientists will perhaps not recognise the Muse, or if they do they may not consider it scientific. Most mathematicians will probably be lost round about now! There is one mathematician/philosopher, Polya, who wrote a small pamphlet called "How to Solve it". In this book he sets out a heuristic approach to solving mathematical problems. If you have not read it, do so, because the term heuristic is partly defined there for mathematicians. http://en.wikipedia.org/wiki/How_to_Solve_ItThere is another term that requires your understanding and that is sophistry. To apprehend it properly you need to contextualise it in analogous thinking. Analogous thinking is evidenced or documented as far back as the early Babylonian / Sumerian civilisations. It represents mans use of symbols both tautologically and iteratively in the process of interacting with space and its inhabitants. To restrict it to symbology is to miss the point. For human consciousness everything is symbolic! Thus for every advance in this regard I do not discover a reality as much as I inherit a cultural reality which I explore and manipulate. I may break out of the cultural wraps I inherit and develop new and mysterious symbolic interaction, which then eventually transform my cultural environs, or I may be imprisoned by them. In any case I am rarely if ever interacting directly with an objective entity sometimes called space. The sad thing is, most scientists , especially empiricists believe that they are! The symbolic set that they have been told allows them to do this is called Mathematics! Unfortunately it does very little in that regard, and is not likely to. Mathematics is completely formal. Now Mechanics is an interesting activity, it usually acts directly on a symbolic space. In so doing it reveals properties that ground any formal definition. . Such properties are usually mused upon into some symbolic entity called geometry.. This then feeds back to direct and inform mechanical processes. From these mechanical interactions we can develop models, usually geometric, that behave pretty closely to the space interaction" modelled". The advent of computers and computer graphics and fractal geometry has made this match pretty darn close! We have gone from analogous thinking to computer graphical representation. Where does sophistry fit in? The kind of expertise that human consciousness brings to make all these models happen and Work requires a great synaesthesia of much data and information. The synaesthetic results in special symbols that allow a human expert to think, to mentally manipulate, to guess , and to extrapolate and interpolate with a high degree of certainty. This set is called sophistry. The set of symbols used by a sophist have a powerful unifying effect. While experiencing one event, the sophist gains insight into how an analogues system or system set should, would or may behave.. By taking this insight through a careful empirical testing sequence the sophist verifies, denies or modifies his intuitive insight. This results in no change or a slight change in the symbol set, or precisely how it is applied. Grassmann is perhaps the author who put this all together most consistently. The amazing thing is that no one had actually done this before, publicly. Grassmann's strategy is clear by now: read widely ingest deeply, strip back to geometrical magnitudes and arithmetic " operations", be inspired by labels that support the geometrical relationships and remind you of the essential dynamic of the geometry. This strategy requires hard work reprocessing the accepted layout and format, the invention of new suggestive labels, the setting down of symmetrical formulas and progressive formula development. The result is a clear, simplified notation that mnemonically guides the expert to the correct formulation for the calculation. But what happened in 1844? Grassmann was stumped! He had no inspiration from his muse! In fact his muse had published in 1843, but Grassmann had not had time to hear or read of it. Hamilton published his major work on Quaternions. Later, in 1870 Grassmann is to write a paper on "the place of Hamilton's Quaternions" in his system.
<a href="http://www.youtube.com/v/Q2FCMjlI9Fc&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/Q2FCMjlI9Fc&rel=1&fs=1&hd=1</a>If anyone can get me a copy of that paper I wold be grateful. In 1853 Hamilton gets to read Grassmann's Ausdehnungslehre 1844. He recognises Grassmann as his master, and strives to rewrite his Quaternions Grassmann style! In the Einleitung Grassmann goes into detail about how he constructs his labels, and why but for now i am going to comment on his application in these 2 translations |
|
|
|
« Last Edit: March 25, 2014, 07:51:33 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #166 on: March 23, 2014, 08:47:01 AM » |
|
Commentary
The inner and outer product of line segments are " inter communicant" . That is they inter communicate , one with the other. The usual word I suspect is "corresponding", but I feel it needs a shake up of the mind!
Both Hamilton in 1831 , in his paper on conjugate functions, or couples; and Grassmann in 1844 were particularly keen to explore the activity of the mind in mathematical or rather algebraic contexts. At the time arithmetic and nalysis or higher arithmetic reigned supreme. Algebra was hardly a subject. Geometry and Analysis after the Cartesian model was the vogue.
However the issue of number created an opportunity for certain philosophers to make a case for a rhetorical discourse which made the human mind clearer to students. If one is being kind one might say that Al Khwarizimi was intending to do this all the while! However we probably have to wait for Bombelli to find an educator serious about Algebra in the rhetorical style with his own inventions. Descartes used algebra but did not really promote it. Consequently we arrive at John Wallis as a serious contributor to the idea of it being a topic. Much of the modern symbology derives from his work.
It is not until Hamilton Grassmann and Boole that a serious subject boundary war developed a niche for Algebra in mathematics, but as I say this was really around the concept of the mathematical mind. Logic, up until this point was the prevailing subject dealing with reasoning, but the increasing use of symbols lead to a confluence with Algebra. Boole attempted to rigorously and mathematically reveal the laws of the mind and how it reasoned. This together with Hamilton's work , also called A Science of Pure Time, and Grassmanns work constituted a full body of work to study, alongside logic, such as that espoused by De Morgan.
The human mind takes a person cantered point of view. In that regard everything has to be relative to the individual. The individual connects to space by choosing points and joining to itself by mental lines. These lines are thus extensions of ones connection to surrounding or interior space.
These extensions are characterised by bounds and orientation and direction and by how they swivel.
But there is a different but allied characterisation: the projections of these line segments onto each other defines a set of projected line segments. The differences are utilised by Grassmnn to create many labelled products. These products, used as specified by him, simplify the process of calculation considerably.
|
|
|
|
« Last Edit: March 27, 2014, 10:30:41 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #167 on: March 24, 2014, 01:16:36 AM » |
|
Commentary
A line segment is the product of 2 points.
The product process imparts a quantity to this magnitude, and the magnitude itself imparts roll, pitch and yaw to the line segment, thus general attitude and orientation in space . To this the observer adds an arrow denoting direction of displacement. For any line segment or arc segment there are only 2 directions of displacement. Firmly attaching this to a line segment creates 2 distinct line segments.
The labelling for all this is
aBC = –aCB
Where B and C are the generating points.
For 3 points we may write
cAB + aBC —> bAC where —> means "is linked to"
The = sign Grassmann used has a complex meaning and it is not numerical equality. Geometrical duality is a possible meaning, and this would mimic the Euclidean common judgement that dual things fit atop each other.
The geometrical space which is the product of the 3 points, is a triangular space. This supports the duality of the side bAC to the other 2 .
Now the lines through these 3 points extend out providing anchor points for all other lines in that specific plane. Within this plane are special lines parallel to the line segments cAB, aBC all these lines identify another point D in the plane that gives a geometric product called parallelogram ABCD. That is to say that the intersection product of cAB x aBC is a point D.
This is crazy talk, because usually onli 1 specific pair of parallel lines intersect at the point D! However either by design or failure to think it through rigorously Grassmann defined all line segments parallel to AB with the same length c , the same fixed direction as " equal" or dual. The effect of this definition in his mind was to allow substitution in the symbolic representation. Thus every line segment pair that meets these criteria intersects in a point D .
This notation or labelling is therefore inherently confusing, but wonderfully flexible. It means that universal statements can be made and local behaviours extended to any parallel region anywhere in space or spacetime.
We have no way of knowing if this is how space behaves in all parts of the universe, but this bare labelling convention means if it does we can symbolise it very concisely.
However the major observation that overlooks this odd feature is that when one goes through the process of solving a geometrical problem trigonometrically, mentally one is only focussing on identities, congrnces and similarities. Thus wherever these parts are in a geometrical sketch is irrelevant to the solving of its length and and angles. Typically one reinserts the calculated values into the actual or real world oriented design. Thus the design, sketch or plan remains unchanged, one just mentally twists and shreds it to derive a metrical solution for its defined parts.
We have used the same labelling to get a handle on 2 things: the geometric product as an area, or rather an Arithmos, a multiple form;; and the intersection product of 2 lines or line segments as a point identified by parallel lines. The second product encapsulates the idea of projection by parallel lines, but it is more general than that, because it allows any 2 non parallel lines to intersect regardless of what they individually are parallel to.
I make the distinction that in a parallelogram ABCD , cyclically arranged points, that AB+ BC is not equal to AD + DC, but Grassmann does not at this stage deal with this distinction. He de facto states they are the same because they can represent the same displacement AC . This is useful iteratively because one can collapse an iterated universe of these relations onto a single displacement! However you lose the distinction of what is mechanically happening at a precise moment in time. On the other hand, one can introduce statistical or probability models into the description to give one mentally a model that can deal with arbitrary non discernible even hidden events.
This is in fact what has been done in Quantum Mechnics. The events are usually beyond our ability to discern. However, because of this extensibility or collapsibility to an end result we can model it as a 2 state process with indeterminate intermediary steps! We usually ascribe this idea to La Grange, which is where Grassmann derived most of his ideas for labelling from.
So for me the difficulty is in the use of the = sign and I typically do not use it in this context. It can lead to procedural errors and misunderstandings. However the point is that Grasmann was setting up a mnemonic system of great complexity and sophistication, so to remove it on grounds of incorrect or unsupported identity is to remove also it's mnemonic role. Often what Grassmann writes down is total nonsense, just like SOHCAHTOA! But it is an an extremely helpful aide de memorie in tackling certain classes of problems.
Having established the full labelling for a line segment, Grassmann to avoid Tedium drops writing its full description out. Instead he focusses on the part he is seeking to derive further. Now when Möbius did this with his Barycentric coordinates I pointed it out, and so do so here. The main difference is that Möbius dropped the labelling in order to forget them. Grassmann forgets nothing, but also often gives two meanings to the same labelling. For him, as the developer this was not a problem, but for you and me as the reader we have to be extremely alert to his thinking! The context helps, but also small seemingly insignificant adjectives or adverbs become crucially important.
|
|
|
|
« Last Edit: March 27, 2014, 10:44:37 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #168 on: March 24, 2014, 03:08:03 PM » |
|
Commentary
The parallelogram product is Grassmanns first product process.. It was dynamic from the start, representing a generalisation of a geometric rectangle construction. Why di it become the outer product?
It has to do with how the product morphs as the line segments rotate relative to each other. Initially the product , on an anticlockwise relative rotation went from no constructible area inhabiting form to a form( a rectangle) with the maximum area inhabited. Then it decreases again. This he linked to a value scale that goes from0 to maximum and then back to 0.
To get it to work computationally for him he had to accept that factors were interchangeable only as the sign changes to its opposite. Geometrically it represented a switch in the direction arrow fixed to one of the line segments. Hardly anyone uses this interpretation nowadays. They prefer to use perimeter travel direction ( clockwise or anti clockwise). Whichever interpretation used the calculator still has to imagine the products as cancelling. In other word the process constructs 2 forms each the signed opposite of the other. The observer has to interpret their significance.
The right angled triangle is crucial to all metric results, but to include it in his method he had to recognise the vertical projection and horizontal construction lines as line segments. In so doing he introduced an arithmetic trigonometric product into the length of a line segment.
aBC could be rewritten as b cosøBC where ø is the angle ( in radians) between bAC and aBC.mdirections of line segments and angle measurement are important.. In fact the rewriting is a bit more complicated for the general triangle and involves the cosine law, but I give the case for a right triangle fulfilling b2= a2 + c2
These line segments vary contrariwise to the initiating ones and do Grassmann called the product they produce an inner product, because they get larger the nearer the initial line segments are together rotationally. The parallelogram they produce is always inside the one produced by the initial line segments, but it is there rotating outwards or apart that caused Grassmann to call them outer products.
Essentially then we have 2 algebraic or symbolic descriptions of the same thing. The different and contrasting multiplication calculus leads to different insights and a way of handling a single form more intuitively in symbolic form. For example if line segments are perpendicular the inner product is 0 at the same time as the parallelogram product is at its maximum. Similarly line segments ar arallel when the inner product is maximal and the parallelogram product is clearly nonexistent!
So now this swivelling behaviour was what Grassmann wanted to set down fully in volume 2 , but he also wanted to give an overview in this volume , because the work was great and he did not think he could achieve it all in detail.
We now move to his overview of his labels for swivelling line segments!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #169 on: March 25, 2014, 06:32:36 AM » |
|
Commentary. We now enter Grassmnns crazy mnemonic world! All the same it is crazy cool! For reasons presumably explained in the body of the text figure 1 is labelled by  • 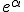 . Figure 1 is a rhombus. There is no connection between any metric on the rhombus and 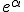 . However, the diagonals of a rhombus do intersect at right angles. Thus the sides project Onto the diagonals as 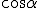 and 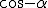 . Now let 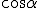 remind you of 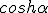 ! But then  has to be measured in radians. These radians are a geometrical circle arc either side of the diagonal ,forming one continuous arc from 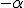 to 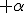 But then we have swung or swivelled one side of the rhombus directly onto the other. So, again, imagine 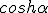 having the same numerical values as ) where now ) is the same angle measured in radians..... Well then I can write 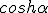 = 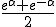 to represent the 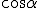 projection! Stare at that a minute and notice that 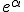 is the swivel in the positive direction by the radian ) of the unit line segment and  is a swing by the same radian arc in the negative direction. Now consider these 2 line segments as labelled by the exponential. Then we can sum line segments in a parallelogram, Grassmann style. Consequently we get the formula for the 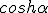 , Grassmann style! This is an analogy with the actual, trigonometric analysis and synthesis. It makes no metric sense whatsoever, but it is a powerful mnemonic aide memoire for the hyperbolic functions. To get the sinh the same figure must be used but the swivelling sides are now in the corner adjacent which represents a 90° rotation in the swivel plane. But because the labelling of points does not change the diagonal is now a subtraction sum, Grassmann style. Adding the 2 hyperbolic formulae gives the asserted form for a swivelling line segment. But it is a tautology because I pointed it out as being in the formula to start with. There is nothing wrong with tautology, by the way, except if you do not recognise it as such. It is a useful tautology because it grounds a symbolic label in a dynamic geometrical experience. However, the underlying trigonometric ratios which are the basis of the analogy do not sum to any exponential function, but they come as close as you like! We know these functions do not sum to the trigonometric function equivalents because ^{2}+(sinh\alpha)^{2}=-1) and  + sin^{2}(\alpha) =1) But within a defined range the hyperbolics are approximated closely by the trigonometric radian functions. So it is not so crazy after all! It is crazy cool! Not only is the mnemonic useful, but the analogy is a useful approximation. This means, thinking geometrically, that a swivelling line segment within a rhombus form is a useful interpretation of the asserted label. We will see how Grassmann goes on to ground the so called imaginary magnitudes in the common circular arc! |
|
|
« Last Edit: March 25, 2014, 10:40:54 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #170 on: March 25, 2014, 08:12:17 AM » |
|
Commentary
Firstly Hermann observes that this result depends on his analysis of the inner product! The swivelling line segment is projecting vertically onto the diagonal of the rhombus. In fact it is clear that he is dealing with the circular arc projections onto the radius in Euler's style. Following Euler gives him all the results he asserts. However, where Ruler uses an infinite series argument , Hermann devises a geometric mnemonic that makes sense of the summation of infinite series in terms of arc segments and line segments.
I do not know if anyone else drew this kind of conclusion from Eulers work on the imaginaries, based on The Cotes De Moivre analysis, and Cotes suggestion, but it would seem not. Wessels seminal paper and the work of Argand , Cauchy and eventually Gauss strongly support this interpretation, but no one, not even Hamilton lays it out as clearly as this!
The reason again is because there are serious procedural difficulties in demonstrating this conclusion. However, using the style of analogous and Mnemonic analysis, set out in helpful labels, the conclusion is almost obvious!
The danger with this style of demonstration is the hidden or unaccounted for parameters. Grassmann has pre digested a lot of material to come up with these labels. But what if he missed ome thing?
Hermann was alert to this difficulty, which is why he required collaborators to check and correct any errors, analyse further and advance the generality of his methods and labels..
So I have come up with a name to distinguish the 2 styles of line segments! The ordinary line segment, that is aBC and the trig line segment , that is bcosøBC, in the context of a t least a pair of line segments intersecting at a point with an angle ø between them and the projecting line segment being of length b.. Ths for bAc and aBC this hold if the angle between them is ø.
The ordinary line segment in the context of a plane figure has a trig line segment compatriot! A line segment has 2 descriptions, an ordinary one and a trig one.
Amazingly the rules of combination and computation are different, especially in the product. Thus Grassmann coined( just as lame as mine I might add. Lol! ) the names outer product and inner product.
Now we move onto the swivelling trig line segments and their labels! Panta Rhei!
|
|
|
|
« Last Edit: March 25, 2014, 09:34:05 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #171 on: March 25, 2014, 09:43:02 AM » |
|
Commentary We have to work on the labels in a certain way. Grassmann took the labels of the ordinary line segments to an extraordinary generality. Once again, I remind us that these are nonsense terms; they label only the fanciful thinking of a whimsical mind. However, they form a powerful mnemonic superstructure for just about all mathematical models in mechanics. It is hard not to credit them with some validity. They do have a validity, but not in mathematics per se. They firm what I call a process arithmetic, written in symbols. Or, if you like, a programming language with its own rules and syntax. So the development that Grassmann treats us to is a development based on trig line segments. But first a result from his ordinary line segment reworking assists. This is the labelling for the intersection product of 2 lines( or line segments). If a and b are labels for 2 lines then the product ab is the parallelogram product or the intersection point product. In this instance we choose the intersection point product. And, since the trig and ordinary line segments are " inter communicant" we can let a and b be trig line segments and the product for the point of intersection remains identical. However the parallelogram product now becomes the inner product. We use the observation that the inner product has virtually the same rules as the usual arithmetic to develop the labels. Firstly we set a• 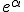 to a• 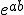 This means that the trig line segment a swings from the position or orientation of a to the position of b around the intersection point of the 2 trig line segments. It should be noted that the trig line segments are rays and so identify a corner angle between them specifically. The other thing to note is the notation result relies on the quantity of angle being 2  , that is from –  to +  . Somewhere along the line we neglect the doubling of the actual angle when analysing rotation!noften, Euler angles "go wrong" because of this oversight. Setting a• 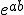 = b expresses that a swings and becomes bThus 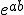 = b/ aThat is the swivel between 2 trig line segments in the same plane is the Quotient or division or rationation of the trig line segments. It is unusual today to think of dividing a magnitude by another magnitude. We think that numbers are the only thing! A quotient is properly a process of comparison and the result is precisely a ratio not a number. In this case the ratio and the exponential are identities. That is we can replace or substitute on for the other.. The concept of comparing the 2 trig line segments focuses on the swivel magnitude between them. There are other magnitudes to compare like length etc but this labelling is comparing orientation. From this Grassmann moves whimsically to the logarithmic form ab= ) Thus he declares the point of intersection to be the logarithm of the Quotient of 2 trig line segments. He points out that the logarithm will have infinitely many values because the product of two trig line segments has infinitely many solutions for the angle between them, in terms of multiples of 2 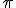 + the angle, However, thinking purely geometrically, the point of intersection of the corner angle, as a point will take infinitely many angles. To specify one angle the containing rays are necessary, alongside the radian measure. |
|
|
|
« Last Edit: March 27, 2014, 10:58:08 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #172 on: March 25, 2014, 08:45:56 PM » |
|
Commentary
So why do I keep pointing out the lack of logical necessity and sufficiency of this method?
Really it goes to the heart of logic. Today we use logic not dialectic, the comparison of two arguments. Today we mistakenly think logic is undefeatably correct. Logic has never made this claim., if it is correct to anthropomorphise logic. The humans that devised logic, including Aristotle, sought only to battle bloodlessly using words, concepts and common intuition. The whole paraphernalia of logic is not often viewed, but for the mst part it involves rendering your debating opponent speechless. Tactics include ad Hominem attacks as well as misdirected attacks or spurious argumentation, ie deliberately misrepresenting your opponents views. The debate held in public would continue until one was unable to answer, or until the crowd decided the victor. You may well imagine, debates were not well attended! If there was no blood sport, not many could spare the time!
Philosophers however refined the force of proportioning evidenced in an argument into a system of syllogisms and dependent clauses with validity proportional to the preceding statements. Deduction and induction were specified and universal logical operators. Thus if a set of statements had this proportional characteristic, it was described as logical.
But not everything we experience can fit into this ordering of presentation and rhetoric. Analogy for example does not follow this system, and yet is the most important form of reasoning we humans use to apprehend the world. Analogous thinking is more often treated as suspect or not dependable, and particularly not proportional to external verification.
To justify an analogy one must compare both the experience and the so called nalogues of an experience. It is thus a subjective determination.
Virtually all of Grassmanns method is based on deep and cogent analogical thinking and insight. However it is hard to justify it by any other means than directly using it as instructed! From the outset Grassmann states this, and this is why his Vorrede takes us on his journey of discovery.
I do not fault the work. Rather it casts deep and piercing light into the way we subjectively process our interaction with space and labels. To see that line segments have a firmly fixed direction, nd that trig line segments also in addition have a firmly fixed plane of swivelling, and that really the logarithm of a quotient of 2 trig line segments is a point with infinite values, a kind of logarithmic Schwerpunkt, testifies to the inviting nature of this system toward creative thought and heuristic exploration.
It is alive, and invigorating, and it leads to deep insights, but then much hard work and rejigging and modification of labels has to be carried out to ensure it works seamlessly.
Grassmann got stuck on the 3 d rotation problem. Rodrigues had a solution in 1840, Hamilton in 1843. Both of these, had he read them would have been sufficient Muse for him to have set out his labels with that case in mind. His system already pointed out the importance of the half angle!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #173 on: March 26, 2014, 02:56:29 PM » |
|
Commentary Reworking part of the earlier transaction to draw out the set up for the second translation on the imaginary magnitudes but more specifically the trig line segment "Multiplication" system, which is really a quotient arithmetic. The uses of  is twofold. The first is just as an identifier. The second however is in its geometrical sense as a measurement of an amount of turn. The measurement scheme or metric chosen is the radian measure.. To make the analogy work the radian measure has to be used both for  and ā. Hermanns delivery of this point is casual, because he knows he is referring to the radian measure, but the reader may not be certain what he means by " the geometrical sense". The other point is that in the rhombus only the angle  us used to derive the magnitudes. Thus the swinging arm for cosh has to change to the adjacent corner to be the swinging arm for sinh.. This is all by analogy with cos and sin. The closeness of the values of sinh and sine in this radian measure is remarkable., but it only works modulo 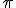 /4 |
|
|
|
« Last Edit: December 02, 2014, 03:06:29 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #174 on: March 27, 2014, 04:45:56 AM » |
|
Commentary Hermnn has looked into the heart of darkness and like me found all our calculus or metrication depends on the trig ratios. But what I did not know was the close relationship between the hyperbolic and the quadratic forms of these trig ratios. From Napier snd De Moivre I knew of the close link between the binomial expressions for the sine ratio nd the exponential ratio; that one curved inside the boundary of the unit circle snd the other spiralled outside the boundary. But I never realised until Euler pointed it out there was a link, an intertwining that hovers around the circle boundary passing in turns inside and outside the disc. Having used the analogy one way, that is to establish a mnemonic for the swing of an ordinary line segment, Hermann now uses the analogy the other way, that is to establish the swing of a trig line segment. At the same time he establishes a quotient calculus. This completes the so called 4 operations of addition and subtraction, multiplication and division of line segments. His analogous arithmetic of line segments he called a lineal algebra. It was a crazy giraffe of a creation. Already it had about 7 different products, and 3 different outcomes for a product!, that is the products went to zero or not according to 3 different rule sets. Also ani commutativity was necessary in one of the product processes. Very strange and initially very troubling! I suppose we all have to grow up sometime! Interacting with space has never bern the Pabulum we get fed in elementary school. Consequently we struggle when we encounter the real processes we have to engage in. However, Hermann deliberately chose the clearest labelling practices to couch his mnemonics in. They were both apt and supportive of intuitive development. Starting with the quotient of 2 trig line segments of the same length swinging through an angle he was able to immediately write this as n exponential form.. This identity between the quotient and the exporntial immediatel meant all summation would be logarithmic. But logarithmic summation is the labelling for multiplication! So now he had another form of product( multiplication) which was entirely arithmetical. The rest relies on definition and consistency in definition. If we do not think too hard it all flows swimmingly! Do not think what the square root of a quotient of 2 trig line segments might be., just realise the special case where the swing is 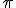 radians and thus half the swing is the square root of the quotient! So how does this quotient get into the exponent of the exponential? I have given this a lot of time and have come to realise that Grassmann has no explanation for this. It is pure Euler! Euler arrives at this by expanding the exponential into a series . Having done that for  he replaces it with a complex magnitude. In so doing he obtains the cosine and sine series in a complex form. http://mathsforeurope.digibel.be/Euler.htmlhttp://www.songho.ca/math/euler/euler.htmlThus Grassmann is saying that this shows 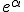 and ) to be identical geometrically: they both mean a line segment is swung through an arc about a centre point! Finally using the rhombus again, but this time to remind you of the sine and the cosine ratios he immediately writes down the form. However he places the ) also before the sine because the sine line segment is a rotation of the cosine one. |
|
|
|
« Last Edit: March 28, 2014, 09:35:55 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #175 on: March 27, 2014, 10:02:52 AM » |
|
Commentary
Grassmann establishes the Magnitude of turn. Thus a/b is the label for the experience of swivelling or rotating in the direction from b to a. That could be clockwise or anticlockwise, but by convention it is anti clockwise. The rays( line segments with direction arrows) pick out a specific corner of the 4. Thus it is not ambiguous in Hermanns labelling system, but nevertheless we use the convention, mostly!
This experience of swivelling has an identified centre of rotation, the intersection point of the 2 line segments. Further, all line segments that lie in this plane and pass through that intersection point will experience that swivel or rotation. Thus Hermann is stating that the notation applies to the rotation of the whole plane!
The quotient label is thus a label expressing plane rotation and specifying the centre and direction of rotation.
Now Grassmann moves on to the Quantity of rotation . The magnitude becomes a quantity when bounds are identified. In this case Grassmann specifies the bounds of the swivel as the line segments themselves. Clearly this specifies a unique swivel from b to a. Thus when it is applied to b the result is a. The general result is just the symbolic form.
Now it strikes me that Clifford Algebra has this magnitude differently( and confusingly) expressed. Check this out.
<a href="http://www.youtube.com/v/sHjXccDAIzw&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/sHjXccDAIzw&rel=1&fs=1&hd=1</a>
You will note, hopefully, the discussion of sin, sinh, cos and cosh reduced to this so called Clifford geometric product! However it is not explained and the only motivation is to multiply it out!
It differs substantially from Grassmanns treatment because it obscures everything to avoid seeming logically inept! Grassmann on the other hand wants everything out in the open, explained with crystal clarity. Thus he suffers the charge of being fanciful, but gains my respect for pointing out precisely what is experienced. Thus I do not fault him or his method. It is an analogous way of thinking and analyis and synthesis that has demonstrable mnemonic and intuitive value.
|
|
|
|
« Last Edit: March 28, 2014, 03:32:53 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #176 on: March 28, 2014, 08:37:02 AM » |
|
This exercise has been very valuable to me. Shaking off the misconceptions about Grassmanns work and praxis reveals a clear picture. The AusdehnungsLehre is simply put part of a programme analysing how humans think. It's real topic is how humans think about solving problems, that is how they think about thinking! Mathematics was " chosen" because it was and still is considered to be the supreme intellectual product of the human mind whilst thinking about space and our interrelationships with it. However, essentially Grassmann fell into this topic of heuristic thought while doing what most mathematicians do: wonder how the so called geniuses solved the mathmatical problems of their day. Basically Grassmann studied the great minds of his day, at least all those he could lay his hands on, which in Prussia were mostly European and French scholars. As he read and learned their ideas he made " crib" sheets, brief notes and summaries to remind him of their methods, advice or examples of how to tackle particular issues. It is these study notes that form the basis of his Analytical and synthetical system. If you are presented with a problem how do you solve it? Grassmann adduced the key ideas required to do just that for a vast range of mathmatical problems. Whereas most of us might learn a direct solution or a general principle of solution or two, Grasdmann constructed a system which was originally intended to be split into 2 volumes. The first volume he called Ausdehnungslehre, and this was really all about line segments. The second volume , I guess he might. Have called Schwenkungslehre, because it was his intention to deal with solutions to rotational problems. His concept in overview was to bring everything together in an accessible form in that volume, providing an easy reference to all results he had discovered and formulated in the process of his research. The two volumes, therefore would have provided the serious student of them with considerable expertise over a wide range of the then known mathematical landscape. Beyond that it would enhance the ability of all engineers and mechanics to formulate solutions to their everyday problems and support them in their research into ground breaking applications to mechanical problems. In this age of steam, electricity and early chemical and industrial engineering the need for a skilled and intellectually ready work force of engineers was paramount. So in essence Grassmann created nothing new in terms of applications of thought to spatial interactions, but what was new was his exposition of how to think about solving mathematical and mechanical problems. Without a broad and deep understanding of the mathematics of his day Grassmnn would not have been able to develop his system of analogous thinking and mnemonic hooks. It may well be that when they fully publish Euler's works that they find that he has written on this topic also, because Euler was a master of clear thinking. However, as far as is known, Hermann Grassmann is the first author to put together such an extensive exposition of human thought process in the mathematical arts. http://mathsforeurope.digibel.be/Euler.htmlWe can characterise the scheme of his approach by commonly used geometrical terms: translation, rotation and reflection. In fact these are less general than his conception, but I mention them to connect his work to the Erlangen movement inspired by Klein as a student of an academic who seriously studied Hetmanns work. What happened to the Schwenkungslehre? I have no idea, because Robert tore up Hemanns planned progression and forced a redaction of the work as previewed by Hermann. In 1861 much was written in a new format that appealed more to mathematicians, of which Robert was no mean slouch, and thus much was redistributed throughout this second version. However the paper on Quaternions perhaps would be most helpful in answering the question. In passing I note that because of Euler's work, Grassmann had the solution to how to deal with a swinging arm in 3d, he just could not see it in 1844 or even until he read Hamiltons Quaternions. It turned out that his exponential form, and his firmly fixed plane of swivelling was all he needed to construct the quaternion solution! When he realised and demonstrated that, he wrote that Quaternions had no more to teach him! As with Möbius he believed his system now enabled him to instruct those who used Quaternions. This may sound arrogant, but as I pointed out, Hamilton on reading the Ausdehnungslehre 1844 recognised this immediately! It took Grasmann another nearly 20 years from 1853 when Hamilton first encountered Grassmnns work to come to the same conclusion! |
|
|
|
« Last Edit: May 08, 2014, 05:30:36 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #177 on: March 28, 2014, 03:39:24 PM » |
|
Hamilton derived a solution for the 3 dimensional swivelling situation. The following is a treatment of that solution which shows a similar approach to Grassmann with regard to the quotient operator, but which does not recognise the value of ordinary line segments and trig line segments. http://www.songho.ca/math/quaternion/quaternion.html |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #178 on: March 29, 2014, 08:27:37 PM » |
|
I want to tackle the rule of anti commutativity. Reviewing Grassmanns introduction to it, I can find no geometrical model that matches it precisely beyond the line segment.AB=–BA
I have puzzled extensively over this rule for a long time, under the misconception that Grassmann saw something in the geometry to inspire his insight. However, understanding his praxis better leads me to conclude that this too is a bit of Grassmann analogising!
In terms of the history of complex numbers Bombelli stands out as the only one to "define" a negative area. Using neusis and his carpenters square he drew conjugate forms as solutions to some of the quadratic equations. In fact he defined the terms conjugate and adjugate for these geometrical forms. In effect, therefore the conjugate of a figure was its " negative" . It allowed for the solution of say x^2 +1 =0. One figure would be above a line, the other would be below that line. Thus x+ y and x- y would form 2 figures conjugate to one another( that is as linear forms in their own right. Set them both =0 and draw the lines on graph paper.) Thus x+iy and x–iy made the same sense to Bombelli, but he was on his own with this! Today we can consider these as vectors along the 2 lines , and the rotation angle between them to be pi/2 a quarter turn rather than a full half turn implied by the concept of negative.
Especially in the the completing of squares, this conjugate representation was helpful in representing the " negative" rectangle or square required to solve the square problem.
Geometrically this was always harder to represent than " algebraically" or in symbols. This is because in the page you have no way of distinguishing a negative value of area! A negative value of volume can be represented, but area , being a surface in a Surface has no orientation to support a negative sense. Bombelli elected to draw a line and draw positive area above it and negative area below it. However he called thise arrangement conjugate, and did not assign a negative sign to the whole form.
The defining of negative in the plane is not so clear cut. Many positive and solvable equations also have squares or quadrature that has the " conjugate" form, in terms of the difference of 2 squares. These Bombelli called adjugate numbers. There was some property of the conjugate numbers he could not apprehend. That property is rotation!
So now, from the outset Grassmann has to pin don this " negative" property.
Switching the order of the symbols in a line segment , and then translating or displacing in that " direction" seems to make sense of the notion of " contra" or opposite. This notion is often simplified to negative, and a single symbol represents it. However it is clear that contra is not simple at all.
The orientation of a line segment is assumed or given. If this is not so, then it literally becomes impossible to assign" contra" any meaning.
Usually orientation in the page is agreed by convention to be horizontal and vertical. The principal orientation is horizontal.
The first line segment is drawn or constructed in the principal orientation. This is so ingrained in us after a while that we will actually rotate a drawing on paper into this orientation.
For any line segment in this orientation we may choose 2 points to mark the beginning and end of the Direction we propose to set as principal or positive. Thus we have a principal orientation followed by a principal direction.
We now move into Relative orientations of line segments. We usually establish a relative orientation by rotating away from( Aus treten!) the principal orientation. But we have 2 rotation options in the plane. By convention and imposition anti clockwise is the principal rotation direction.
Using these 3 principals we should be able to communicate a precise drawing plan, or construction instruction to another person.
The problem arises with the introduction of contra.
To construct a contra line we first have to construct a defining principal line segment or set of relative principal line segments. Contra is defined relative to these principal line segments. What is usually missed is the definition of a " contra" area or form.
In both the trig ratios and coordinate geometry it is natural to define regions of negativity, but these regions themselves are not defined as negative! The usual patter is that a line measurement( axial) goes negative or a function value goes negative in a specified region. The region itself is not considered in these definitions.
Bombelli could define 2 regions in this coordinate system as negative and the other 2 as positive. They are vertically opposite geometrically, contrariness is to the " side" of the positive regions not diametrically opposite!
In the light of all this Grassmanns notion of firmly fixing directions to line segments has consequences.
Firstly having defined the principal Directions how do you define the product of these line segments?
For example if AB and BC are principal and relative principal directions what is AB x BC compared to AB x CB?
Arithmetically one should be contra the other, but geometrically what has altered?
In the drawing nothing really. The difference is in the observers procedural behaviour relative to the drawing. This is neatly encapsulated in the symbols, but obscure in the diagram!
So how do I proceed? Grassmann states he carefully multiplied all line segments bearing fully in mind their " relative" directions. But how do we determine relative direction?
Strictly speaking we should do this relative to the conventions, but almost always we lose connection to these principal directions as we swing the drawing round to complete the construction. Then we question the validity and usefulness of the convention!
So, specifically Grassmann states that symbol interchange accompanies sign switch, that is the factors of a product of ordinary line segments ( the parallelogram) are the line segments that actively construct that form. Switching those line segments results in a contra form being constructed.
The problem is when you switch the line segments the only conventional meaning for that is that the principal line segment and the relative line segment change. When you do that construction you do not get a clear " negative" in the sense of a region separate and distinct from the initial region, you get a differently " oriented" form that overlaps. It is in fact a rotation out of the plane and back into the plane about a diagonal axis between the two. It is in fact a conjugate reflection in this axis.
That is fine, if that is what is meant by contra geometrically, but arithmetically the 2 forms are defined as cancelling each other. While the overlap would fit this geometric description, the remaining parts in the Gmomon or conjugate are vertical opposites either side of this gnomon diagonal. What is the geometric significance of that, and are we obscuring a geometrical or mechanical phenomenon by reducing this to 0?
|
|
|
|
« Last Edit: May 08, 2014, 05:49:05 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #179 on: March 31, 2014, 03:13:26 AM » |
|
Commentary
Clarifying what anti commutativity is not geometrically leaves one possible solution as to what Grassmann was observing.
First a brief introduction to cyclic quadrilaterals.
<a href="http://www.youtube.com/v/ylXdx2qv_FQ&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/ylXdx2qv_FQ&rel=1&fs=1&hd=1</a>
Now parallelograms as a rule are not cyclic, so my point is not about the theorem properties of a cyclic quadrilateral, but about how we label a quadrilateral in particular.
Underlying all math is the trig ratios. These ratios are extended by the CAST rules into all quadrants of the circle. While not every quadrilateral has 4 points on a circle , we still tend to label the points cyclically..
The next point is to understand vertauschen and umkehren in relation to trigonometric conventions.
Simply put these ideas combine in the practice of cyclic order interchange. This is a basic "symmetry " process used to prove similar results in specific circumstances. In fact it relies solely on the observer realising their freedom to label corners cyclically starting wherever they choose, certain demonstrations are independent of the geometry at a locale because they rely on the consequences of procedures not on specific measurements..
Given that we have principal orientation, principal directions and principal rotation it is usual, once a figure is constructed, to leave the figure untouched in the plane. In this way the figure itself serves as a mark or reminder of these Principals.
For a drawn or constructed parallelogram ABCD what can we interchange? Nothing of the lineal symbols but everything of the labels for the points!
The question is how should we interchange the points?
It is usually but not always specified that we change the point labelling cyclically.
Thus the same ,fixed oriented parallelogram in the page may no be labelled DABC, or CDAB, or BCDA. This is an anti clockwise cyclic order inter change. The principal orientation has not change, nor has the relative principal rotation for adjacent sides. What has changed is the relative principal direction of at least one of the sides at each interchange .
This effect only applies precisely to parallelograms.
Nothing but the labels have moved, yet according to the strict formalism, what was a positive product now becomes a negative product!
In this case we are introducing a negative sign, not to show that the figures principals have changed, but that we have changed our labelling of its principals!
This has 2 effects: one we appear to cancel something which has not changed, and contrariwise what is fixed appears to rotate round its perimeter! If you can imagine the track of an early world war 1 tank you will have the movie of what I refer to.
Dynamically then, and Grassmann was from the outset dynamic, the label interchanging cyclically is the only process that I understand that introduces a negative sign into one of the factors, thus supporting his assertion ab= –ba.
If a was in the principal orientation with the principal direction and b in the relative principal rotation orientation with the principal direction, specifically in a parallelogram interchanging cyclically in the principal rotation would bring symbol a into the relative principal direction position and b into the principal orientation with the principal direction now pointing in the contra direction. The product of these 2 factors must now be deemed negative to the initial product.
As you can see this is a purely symbolic device . It's power is to arithmeticalky ignore certain products but also to encode rotational information of a special kind.
Of course, as soon as you introduce the trig line segments, this kind of interpretation has to be ignored because the explicit trig functions or ratios introduce their conventional sign rules as in CAST.
Finally, using trig line segments but with swivelling of these line segments relative to the principal orientation allowed, the rules change again back to normal arithmetic. The swivelling itself introduces principal relative rotation as a presupposition, before any relative rotation against ( relative to) the swinging arms!
<a href="http://www.youtube.com/v/PFb4lgdB2aI&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/PFb4lgdB2aI&rel=1&fs=1&hd=1</a>
Note that cyclic order interchange does not give a negative area! This is because in a triangle no lines are in the contra direction! That is the principal orientation is not utilised in any other part of the figure.
From this it is clear that only figures which are constructible from parallelograms will have anti commutativity!
Note also how shifting the paper does not change the principals, rather it indicates the mental processing of the observer. That mental processing per force involves rotation relative to the observer.
<a href="http://www.youtube.com/v/sd10yVm6y_E&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/sd10yVm6y_E&rel=1&fs=1&hd=1</a>
This is the missing part of any notational or labelling system which Grassmann managed to capture in his labels, and Hamilton only captured by coordinate transformation!
Because Grassmann could notate rotation by the correct choice of labelling( ie cyclic ordering) his work was label wise much simpler and cleaner.
|
|
|
|
« Last Edit: March 31, 2014, 04:41:38 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










