END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

A Matchmaker Mandelbrot zoom into Portal II.

Points for which the dynamics lacks attractors are the black-with-red-galaxies background. The coloring is by average separation of the two critical points over one million tandem iterations: the greater, the redder. Note that some red patterns recur in a chain heading into a valley, almost like seahorse centers would in a "normal" Mandelbrot. I continue to hope to find some way of processing these orbits that will reveal more structure. In theory, seahorse-like structures fill this void, but completely fill space making it hard to actually visualize them. If there was a way to color points based on which bud the point was ultimately attached to, in theory this would give each of these structures a distinct color -- but every point would be near many colors, so you'd still just get a hash. Some way of weighting the pixel color perhaps.

I have a few ideas; for example, "pseudoperiods" or "resonances", finding almost-periodic behavior in the orbits. Near one of these buds, a critical point might be expected to come close to periodicity with the period of that bud or a multiple, for instance. Another possibility I intend to try is coloring by the orbit centroid real or orbit centroid imag or orbit centroid argument, etc.; the orbit will be dense in the entire Riemann Sphere but it may be more concentrated in some places than others, in a certain sense, landing near some points more frequently than others. Such a method might make visible structure in the Julia set, as well; sure all these Julia sets are geometrically the same, the full Riemann sphere, but the dynamics differ from one to the next, and perhaps there's a way to expose that visually.

The other layers are the usual for these: one (pinks and whites and pastel purples) for parameters with a single attractor, one (purple) for parameters with two attractors, and one last one (greyscale) for parameters with a single attractor that is additive and colored by the difference between the smoothed iteration values for the two critical points, thereby making the filament structures more visible, especially in the higher-iter regions close to the boundaries of the buds.

The big double-headed bud has period 3; the two large purple overlap regions are one with periods 1 and 3 and one with two period 3 attractors. The largest purple minibrot inside the big bud has a period 4 cardioid.

In a way, this is like a through-the-looking-glass version of the big upper bud on the normal Mandelbrot, only with the biggest minibrot moved into the bud, and the bud convoluted and split and made to overlap itself and the cardioid.

The self-overlap is dynamically interesting; anywhere nearby there is a single period-3 attractor, but crossing into the overlap region causes a second such attractor to materialize. If the parameters are varied along a circuit that remains within the pink zone and crosses the purple zone, then loops back beneath it, then returns, then the attractor is joined by a second, the first becomes unstable and vanishes, and then the second slowly transforms into the first. The point at the bottom of the football-shaped overlap region represents a kind of bifurcation where the single attractor of period 3 splits in two.

This has implications for creating Julia set animations of generic mappings. Naively you might think to give each attracting basin a color scheme/gradient and animate away, but how to you identify what is the same basin from one frame to the next? Of course you can locate the attractor and color the same as the attractor in the last frame that came closest, or some such, but if you went around the loop described above, at the end the two basins would have swapped gradients! Fixing this is difficult; in fact, it requires a way to decide the color scheme that is determined only by the one frame, and yet will change continuously rather than discontinuously from frame to frame. 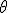It turns out that using a coordinate (r, , x, or y) of the centroid of the attractor as an input into the coloring works relatively well; the coordinate in question will vary continuously. This still has issues; the centroid can speed up abruptly around bifurcations at times, causing rapid color shifts in the animation. I'm still researching this.

As always, the image has a 2048x1536 version available by following two links and is freely redistributable and usable subject to the Creative Commons Attribution license, version 3.0.

Detailed statistics:

Name: Multibud
Date: June 26, 2009
Fractal: Matchmaker Mandelbrot set
Location: b-plane; a = 0.53256 + 0.31163i
Depth: Very Shallow
Min Iterations: 64
Max Iterations: 1,000,000
Layers: 4
Anti-aliasing: 3x3, threshold 0.1, depth 1
Preparation time: 2 hours
Calculation time: 3 days (2.5GHz dual-core E5200)

Very nice! Glad to see Pauldelbrot's posts coming back
@BradC: search Pauldelbrot's posts for "Matchmaker", I think it's just another rational map (not z²+c, but a little bit more complicated with a few more parameters)

The rational map is and has critical points at . The critical points' fates are more-or-less independent of one another, so any two quadratic Julia set basins can be produced, and will together have to tile the Riemann sphere with their connected components. When there's only one attractor, if its period is 1 the Julia set is a dust and if its period is greater than 1 the Julia set is again the result of tiling the Riemann sphere with the connected basin components.

The Mandelbrot view divides into points where there are no attractors (black and red here), points where there's one (most of the pinkish bud interiors, with filaments) and points where there's two (solid purplish regions with no filaments, where buds visibly overlap).

When there's only one attractor, at least one of the critical points must be in its immediate basin (by a longstanding mathematical theorem in this area of study) but the other is free to wander, and wander it does, sometimes hitting the Julia set itself. As it moves among basin components and crosses filaments of the Julia set as the parameter varies, structures from the Julia set, including filaments, become echoed in the Mandelbrot view. The layer that uses the difference between the two critical points' smoothed iterations enhances the filaments' visibility nearer the bud edges, because that difference becomes large when one critical point is almost right on the Julia set and the other is further away from it.

There's a more detailed explanation at the link labeled Portal II in the original post. To actually understand the math, prove that theorem I mentioned, or similarly is rather more involved, but The Beauty of Fractals may help with that, and reference works on topics such as complex analysis.

Re: my hiatus -- I get busy with other things during the summer.

Well, because there are two parameters, the Mandelbrots for these are four-dimensional, and three-dimensional slices could be rendered with the right tools.

No idea. Perhaps someone should try it and see?

Thanks.