|
M Benesi
|
 |
« on: October 23, 2010, 06:50:13 PM » |
|
I can't believe how obvious the formula is after I discovered it.... There are 2 main varieties, although I prefer the one I'm posting images of. I stumbled across this formula while playing around with a new fractal type, and decided to apply what I discovered to my old complex compound formula. You can redo the code in trig form if you want, using dual-complex numbers works about 2 times as fast on my comp... I'd like to add that my other formula, which combines the 2 3d Mandelbrot varieties, produces far more interesting fractals (at least for higher n z^n). I'll post it beneath the images... r1=sqrt(sqr(sy)+sqr(sz)); // you can do x and y values here instead and generate a different fractal
// gotta make sure you change the rest of the formula to match if you decide to do so
// I prefer the way this looks, for whatever reason... anyways-
victor=complex(sx,r1)^n;
bravo=complex(sy,sz)^n;
r3=part_i(victor)*r1^-n;
nx=part_r(victor);
ny=-abs(r3*part_r(bravo));
nz=-abs(r3*part_i(bravo));
//Then you add in your regular x pixel component and the absolute value of your y and z pixel components:
sx=nx+ (pixelr);
sy=ny+ abs (pixeli);
sz=nz+ abs (pixelj); //these values are the starting values of the next iteration...
bailout= abs(sx)+abs(sy)+abs(sz) // or square 'em if it makes you happy... doesn't make a difference to me
side:  top:  rear:  front:  This formula is produces way cooler fractals. While it skews away from the Mandelbrot type a bit, it has more variety... it's just more interesting. victor=complex(sx,sqrt(sqr(sy)+sqr(sz))); //the major difference in this formula is that it rotates sx
bravo=complex(sqrt(sqr(sx)+sqr(sy)),sz); // vs sy and sz, but then calculates the sy and sz values
cramden=complex(sx,sy); // using the other base mandelbrot formula... Makes an AWESOME fractal
// you can also switch which part you do the stuff with if you so desire...
r1=cabs(cramden)^-n;
victor=victor^n;
bravo=bravo^n;
cramden=cramden^n;
if (r2mode) { //It's neater when you exchange the y and z parts, however I put this switch in
nx=part_r(victor); // so I could do it the other way as well
nz=-abs(part_i(bravo));
ny=-abs(part_r(bravo)*part_i(cramden))*r1;
} else {
nx=part_r(victor); //this is the more interesting variety, the default...
ny=-abs(part_i(bravo));
nz=-abs(part_r(bravo)*part_i(cramden))*r1;
}
|
|
|
|
« Last Edit: October 29, 2010, 08:38:01 PM by M Benesi »
|
 Logged
Logged
|
|
|
|
|
Paolo Bonzini
Guest
|
 |
« Reply #1 on: October 23, 2010, 11:33:06 PM » |
|
nx=part_r(victor);
ny=-abs(r3*part_r(bravo));
nz=-abs(r3*part_i(bravo));
sx=nx+ (pixelr);
sy=ny+ abs (pixeli);
sz=nz+ abs (pixelj); //these values are the starting values of the next iteration...
Why the abs and (for ny and nz) the negation? The formula without them is, if I did my math right, r1=sqrt(y^2+z^2)
sx = x^2-y^2-z^2 + pixelr
sy = 2*x*(y^2-z^2)/r1 + pixeli
sz = 4*x*y*z/r1 + pixelj
which embeds the 2d mandelbrot. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
M Benesi
|
 |
« Reply #2 on: October 24, 2010, 12:13:40 AM » |
|
Why the abs and (for ny and nz) the negation? The formula without them is, if I did my math right, It does look like you get a standard 2d cross section if you don't do the abs/negations, however there is something I've got to look into further before I say anything else (perhaps in a couple hours I'll follow through, have to do a few things now); ooohhh I remembered: You are NOT going to get a 2d Mandelbrot cross section with x + i sqrt(y^2+z^2), because you are always taking the absolute value of the y component :sqrt(y^2) = |y| .... You could set the value to y's sign though but then you get huge missing chunks out of your fractal (I've tried it with: sign of y, sign of z, sign of y+z... all are discontinuous: huge slices cut right out of the fractal). Come to think of it, I may not be justified in calling this a 3d Mandelbrot, as it's more along the lines of a 3d Burning Ship fractal. The best looking 3d rotation based fractal to date is the "beautiful fractal" which is the formula I posted at the bottom of the first post in this thread. It's got tremendous variety for all z^n... and I extended it to 4d... totallllly amazing. |
|
|
|
« Last Edit: October 24, 2010, 02:25:20 AM by M Benesi »
|
 Logged
Logged
|
|
|
|
|
M Benesi
|
 |
« Reply #3 on: October 24, 2010, 07:06:05 PM » |
|
I did go ahead and set up the fractal with 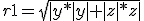 (if you can tell, I take the absolute value of all the variables so I don't get an imaginary root... but what the heck, ehh? maybe I should make it imaginary... if it was imaginary... hrmm interesting...) if (y+z<0) then r1=-r1.. which doesn't reduce to a 2d Mandelbrot (while doing something similar with sqrt(y^2+z^2) gives you a discontinuous fractal). Still need the abs/negation to get the nicest fractals, any which way you do it, although the following method works: r1=sqrt(sqr(sy)+sqr(sz));
if (sy>sz) {
z1=complex(sx,r1)^n;
r3=r1^-n;
} else {
z1=complex(sx,-r1)^n;
r3=(-r1)^-n;
}
if (sy*sz<0) {
z3=complex(sx,-r1)^n;
r4=(-r1)^-n;
} else {
z3=complex(sx,r1)^n;
r4=r1^-n;
}
z2=complex(sy,sz)^n;
nx=part_r(z1);
ny=part_i(z1)*part_r(z2)*r3;
nz=part_i(z3)*part_i(z2)*r4;
Then add in pixel components. It's still nicer if you abs/negate it however. |
|
|
|
« Last Edit: October 25, 2010, 12:02:19 AM by M Benesi »
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #4 on: October 28, 2010, 06:59:08 PM » |
|
The formula in the first post produces one of the most interesting power 2 bulbs i have seen! It has similarities with Msltoes symmetric variations. Without these absolute (foldings?) it is a cosine bulb, that is what i discovered.. but maybe i did something different like always  It seems that the search for a holy grail has become the direction of combining the box and the bulb somehow, the "boxers" are adding rotations and the "bulbers" more foldings  A detail of the power 2 bulb: <img src=" http://www.fractalforums.com/gallery/3/1127_28_10_10_6_46_52.jpeg" /> PS: i attached the power 2 formula for M3D if someone is interested, hope you dont mind. |
|
|
|
 Logged
Logged
|
|
|
|
|
M Benesi
|
 |
« Reply #5 on: October 29, 2010, 05:38:34 AM » |
|
Thanks Jesse! The first formula in the first post is the 3d variety of the Burning Ship fractal (without the -y component as I set y to all positive in the equation). The Burning Ship fractal is simply a 2d Mandelbrot with that uses the absolute value of the real and imaginary components each iteration... ... it's like a Mandelbrot without +/-. As the formula produces an EXACT replica of the burning ship, this tells us that the only thing we need to do is assign signs correctly, like I did in that other thread, to make a perfect 3d z^2 Mandelbrot with no singularities (it's in the "singularity" thread in this subforum). The second formula (first post) though... now that is fricken awesome. Some buildings in the z^4 version:   It is just awesome.... Although now that we have a 3d Mandelbrot that works for z^2,6,10... and all odd n, I found us some seahorses (z^6 though, should search the same location in z^2, as that is where they might be):  |
|
|
|
« Last Edit: October 29, 2010, 05:43:59 AM by M Benesi »
|
 Logged
Logged
|
|
|
|
|
M Benesi
|
 |
« Reply #6 on: October 29, 2010, 06:19:42 AM » |
|
But none of those is worthy of the true power of the 2nd formula. The face of Anachranox (4d) is:  |
|
|
|
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #7 on: October 29, 2010, 04:30:26 PM » |
|
2 questions about the 2nd formula, that starts with: victor=complex(sx,sqrt(sqr(sy)+sqr(sz))); //the major difference in this formula is that it rotates sx
bravo=complex(sqrt(sqr(sx)+sqr(sy)),sz); // vs sy and sz, but then calculates the sy and sz values
cramden=complex(sx,sy); // using the other base mandelbrot formula... Makes an AWESOME fractal
// you can also switch which part you do the stuff with if you so desire...
r1=cabs(cramden)^-n;
What computes the cabs function? I took in my first attempts the realpart of bravo, seems to make sense... And the pixel addition is like in the first formula with abs on y and z? This produces some weird and wired stuff, has to explore more until i could say what formula i like more. Two images of the second formula, first without changing y and z, and the second with changing y and z (and with my assumptions about the 2nd formula): |
|
|
|
 Logged
Logged
|
|
|
|
|
M Benesi
|
 |
« Reply #8 on: October 29, 2010, 08:33:21 PM » |
|
What computes the cabs function? oh, sheesh, didn't even think of explaining that portion... z = complex (x,y) creates a complex number z= x + i y cabs (z) computes the absolute value (magnitude) of a complex or quaternion number in ChaosPro. So if z= x+ i y cabs(z) = 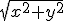 And the pixel addition is like in the first formula with abs on y and z? Yes.  Although I am thinking about trying the sign assignment method that works for the first formula (making the Burning Ship into z^2 Mandelbrots) and seeing what it does with the second formula. I like the switched y and z component formula better than the "normal" method as well (it produces interesting patterns).
|
|
|
|
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #9 on: October 29, 2010, 10:20:55 PM » |
|
Thank you, it is nearly selfexplaining but i wanted to be sure before i make a formula.  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
visual.bermarte
|
 |
« Reply #10 on: October 30, 2010, 05:17:51 PM » |
|
<a href="http://www.youtube.com/v/Zb2BxD9hKtw&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/Zb2BxD9hKtw&rel=1&fs=1&hd=1</a>
|
|
|
|
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #11 on: October 30, 2010, 06:27:47 PM » |
|
Amazing, is this a julia animation from the first formula?
It shows nice attributes of this formula, i still dont know if i like the second one more or not...
nevertheless i attached the power 2 version of the second one with changed z and y.
|
|
|
|
 Logged
Logged
|
|
|
|
|
bib
|
 |
« Reply #12 on: October 30, 2010, 06:44:29 PM » |
|
Jesse, I just noticed you've attached some new formulae here. Are there any others I might have missed recently??
|
|
|
|
|
 Logged
Logged
|
Between order and disorder reigns a delicious moment. (Paul Valéry)
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #13 on: October 30, 2010, 06:48:17 PM » |
|
Jesse, I just noticed you've attached some new formulae here. Are there any others I might have missed recently??
Nope  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
bib
|
 |
« Reply #14 on: October 30, 2010, 06:57:00 PM » |
|
yes.  new M3D is really fast.Thanks Except hard shadows  This is off-topic, but Jesse what do you recommend to calculate them more quickly? |
|
|
|
« Last Edit: October 30, 2010, 06:58:50 PM by bib »
|
 Logged
Logged
|
Between order and disorder reigns a delicious moment. (Paul Valéry)
|
|
|
|


















