knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #15 on: September 30, 2011, 10:52:21 PM » |
|
You could also try: munion(a,b,alpha){
1/(1+alpha)*(a+b-sqrt(abs(a*a+b*b-2*alpha*a*b)))
}
mintersection(a,b,alpha){
(0.25+0.5*alpha)/(1+alpha)*(a+b+sqrt(a*a+b*b-2*alpha*a*b))
}These are smooth variants of min and max operation. alpha should be in the interval [0, 1]. A value of 1 gives the same results as min and max. I found those formulas some time ago in a document about implicit surface modeling and rendering. I will add the reference if I could retrive it. |
|
|
|
« Last Edit: September 30, 2011, 11:15:36 PM by knighty, Reason: Another silly mistake »
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #16 on: September 30, 2011, 11:13:59 PM » |
|
Ooops! These operations actually give smooth distance field. You will see the difference only when you add some value to the DE:
"munion(a,b,0)" will give the same result as "min(a,b)" but "munion(a,b,0)-0.5" is different from "min(a,b)-0.5".
|
|
|
|
« Last Edit: October 01, 2011, 04:23:16 PM by knighty, Reason: yet anoteher silly mistake »
|
 Logged
Logged
|
|
|
|
|
Syntopia
|
 |
« Reply #17 on: September 30, 2011, 11:45:11 PM » |
|
I realized that the method I posted earlier had some serious drawbacks. It is dependenT on the detail setting (minimum distance stopping treshold), so it is not a proper distance estimate. It also scales poorly for multiple objects (since you need to do all-pairwise distance products). I did some Googling and found out that blending was actually already described in John Hart's original zeno paper: http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.48.3825(Soft Metablobbies section) Hart's method is local meaning you can define a radius outside which nothing will be affected. It also scales nicely to multiple objects. #include "DE-Raytracer.frag"
uniform float R1; slider[0.1,1.1,2.3]
uniform float T; slider[0.1,1.1,2.3]
uniform float Dist; slider[0.1,1.1,2.3]
// some primitives from Quilez's lib
float maxcomp(vec3 a) { return max(a.x,max(a.y,a.z)); }
float sdToBox( vec3 p, vec3 b )
{
vec3 di = abs(p) - b;
float mc = maxcomp(di);
return min(mc,length(max(di,0.0)));
}
float sdSphere(vec3 p, float s) { return length(p)-s; }
// Hart's blending function
float CR(float r, float R) {
float rR = clamp(r/R,0,1);
float rR2= rR*rR;
return 2.0*rR2*rR-3.0*rR2+1.0;
}
// The function proposed by Knighty.
uniform float alpha; slider[0,0,1]
float munion(float a, float b, float alpha){
return 1.0/(1.0+alpha)*(a+b-sqrt(abs(a*a+b*b-2.0*alpha*a*b)));
}
float DE(vec3 p) {
float de1 = sdToBox(p-vec3(Dist,0.0,0.0),vec3(0.1));
float de2 = sdSphere(p-vec3(0.0,0.0,0.0),0.1);
//return munion(de1,de2,alpha)-0.5; // <-- for trying Knighty's approach
// Sum primitives
float sum = 0.0;
sum += CR(de1,R1);
sum += CR(de2,R1);
// ... and their radii
float radiSum = R1+R1;
return (2.0/3.0)*(T - sum)*radiSum;
}
Ooops! These operations actually give smooth distance field. You will see the difference only when you add some value to the DE:
"munion(a,b,1)" will give the same result as "min(a,b)" but "munion(a,b,1)+0.5" is different from "min(a,b)+0.5".
You want to subtract something from the 'munion', right? I tried your method - as might be seen on the picture below, it is a global method, so the sphere and box will change shapes also farther away from the melting point. |
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #18 on: October 01, 2011, 04:22:08 PM » |
|
You want to subtract something from the 'munion', right? I tried your method - as might be seen on the picture below, it is a global method, so the sphere and box will change shapes also farther away from the melting point.
Yes, I was a little bit confused because it has been a long time since I've played with it. They are actually called R-functions. See for example this paper or this document. (corrected the previous post  ) |
|
|
|
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #19 on: October 03, 2011, 05:19:02 PM » |
|
Had some problems with a quick implementation of some of the suggested formulas, so i did some own tests and this is what i received so far for the min-combination of distance estimates:
delta1 = Min(0, DE1 - DEcombSmooth);
delta2 = Min(0, DE2 - DEcombSmooth);
DEtmp1 = DE1 + delta1 * (DEcombSmooth + delta2) / DEcombSmooth;
DEtmp2 = DE2 + delta2 * (DEcombSmooth + delta1) / DEcombSmooth);
DE = Min(DEtmp1, DEtmp2);
And the pic:
|
|
|
|
 Logged
Logged
|
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #20 on: October 03, 2011, 05:21:09 PM » |
|
And with a linear combination:
DEtmp1 = DE1 + Min(0, DE2 - DEcombSmooth);
DEtmp2 = DE2 + Min(0, DE1 - DEcombSmooth);
DE = Min(DEtmp1, DEtmp2);
The non-linear method had a DEcombSmooth value of 3, so the effect is not very big compared to the linear one that had a value of 1...
where DEcombSmooth is the absolute distance of the overlap.
|
|
|
« Last Edit: October 03, 2011, 05:38:33 PM by Jesse »
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #21 on: October 03, 2011, 08:37:34 PM » |
|
What about the blobby method?  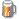 |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
Jesse
Download Section
Fractal Schemer

Posts: 1013
|
 |
« Reply #22 on: October 04, 2011, 08:05:12 PM » |
|
What about the blobby method?  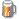 The one and only one, ehmm lets see... dunno whats about it  I just tried Hart's method like in Syntopias code, but have to figure out how to get a general working version with T and other parameters... by now i got only something that looked like my linear version, but it should get better than that. The non-linear version i posted is more like knighty's one, but it might be more easy to implement in a general way, at least for me. Doc, my bulb behaves blobby: |
|
|
« Last Edit: October 04, 2011, 09:28:19 PM by Jesse, Reason: holes in the brain? »
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #23 on: October 04, 2011, 10:17:02 PM » |
|
It looks really awesome as is! Ideal for crazy movies with semifluid fractals! lol  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
hobold
Fractal Bachius

Posts: 573
|
 |
« Reply #24 on: October 04, 2011, 11:46:41 PM » |
|
The trouble with "blobby" blending, regardless of the exact implementation, is that it is always a smoothing operation that tends to drown fractal detail (all small details, in fact, like sharp cusps and ridges and edges). So this kind of thing can only enrich fractal construction in the sense that it can selectively remove the "fractal-ness" in some places.
|
|
|
|
|
 Logged
Logged
|
|
|
|
fractower
Iterator

Posts: 173
|
 |
« Reply #25 on: October 05, 2011, 12:31:11 AM » |
|
I have been playing with combining 2 or more escape time fractals which are spacially seperated.
Assume the origins of the fractals are O1 and O2 respectively. The first step is to calculate the weight to be applied to each fractal.
W1 = exp(-a1 * |z-O1|^2) / ( exp(-a1 * |z-O1|^2) + exp(-a2 * |z-O2|^2))
W2 = exp(-a2 * |z-O2|^2) / ( exp(-a1 * |z-O1|^2) + exp(-a2 * |z-O2|^2))
W1 + W2 =1. The a terms provide a zone of influence. A should be small enough so that the transition is not too abrupt.
Calculate z1 and z2 for each fractal then combine
z_new = W1*z1 + W2*z2.
I have found it best to keep the fractals seperate by at least the escape shell. If the exp is too abrupt, 1/|z-O2|^n will work but n must be greater than the power term in the fractal. For example an 8th order mandelbulb will need an n of 9 or more.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|


















