Ausdehnungslehre 1844
Section 1
The Extending Magnitude
Chapter 1
Addition and Subtraction of the simple extensive/ extending Magnitudes of the former Step/ rank/ Stage or the Line Segments§15. If the continuous creating whole of the line segment comes to be thought interrupted within, broken underfoot in its waygoing , then around hereconcording, continuing forward again to come to Be, thusly appears the complete line segment as knitting of 2 line segments, which continuously close themselves up besides one another , and from which the one appears as continuing forth of the other
Both the line segments, which the limbs of this knitting build a represention of are " in the same sense" created whole(§8), and the output result is the knitting from the beginning element of the former to the end element of the latter, if both continuously in one another are " laid" ,that brands, are so presented that the end element of the first at the same moment is the beginning element for the second.
Forward running we besigned the line segment from the beginning element

( compare with fig.2) to the end element

with [


], [


] and [

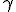
] are in the same sense created,
Thus is [

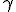
] the output result of the above indicated to one side knitting, if [


] and [

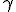
] are the limbs.
We have already (§8) concordingly demonstrated above, that this knitting, there it represents the unioning of The" in like sense created whole" magnitudes, as Addition, and their intercommunicant analytical unioning as subtraction apprehended must become,
And therehere all rules of these knitting artforms for it empowers.
We have here still only the centrally acting assignings concordingly to demonstrate, which the negative magnitude upon our field of study achieves. Specifically , around the initial , the assigning of the subtraction Side by side like showing to make to us , thusly we can thereout that
[


] + [

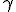
] = [

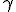
] exists,
Thus directly [


] and [

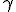
] in like sense created are, we can the conclusion draw, that plainly thusly generally
[


] = [

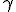
] – [

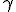
] exists( compare fig.2)
Therefore, that brands, if we now to us the In the subtraction usual nomenclature serve up,
" the remainder is, if minuend and subtrahend with their end element one lays onto one another, the line segment is from the beginning element of the Minuend to the element of the Subtrahend"
One sets in the latter format

and

identical, thusly one outwardly holds
[


] = [

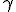
] – [

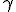
]
That brands, like Null!
Further is everyway pleasing of the label of the negative line segment.
(–[


]) = 0–[


] = [


]–[


]= [


]
That brands, the line segment [


], which to an other [


] its label concording to (§13) running into against set is, appears also in its relating to the Addition and subtraction as the running into against set magnitude to that one.
There at last now.
a + (–
b) =
a –
b exists.,
Thusly one has , if [

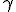
] and [
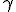

] in the running into against set sense created whole are
[

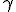
] + [
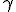

] = [

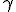
] +(–[

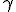
]) = [

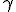
] – [

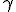
] = [


]
That brands, if also both line segments are created whole in the running into against set sense, their Sum is the line segment from the beginning element of the first to the end element of the second continuously laid besides them.
And we can this result with the above grabbing together summary, declare
" if one knits together 2 like-artformed line segments continuously, that brands so knitted that the end element of the former becomes the beginning element of the latter, thusly the Sum of both is the line segment from the beginning element of the former to the end element of latter.";
And in which entity it as Sum is besigned, thusly it should lay therein expressed, that all rules of addition and subtraction for this knitting style empower.
Still I want to herebesides have a Following to close, which for the wider development, abundantly fruitful is, specifically that , if the bounding elements of a line segment in the same System themselves both around a like line segment vary , then the lying between the 2 new bounding elements line segment to the former is like.
In practice let the originating line segment be [

] ( compare fig3) and [
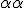
'] = [
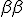
']
Thusly is to show, that if all named elements are related to the same system
[
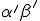
] = [

] be.
But it is [
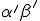
] = [
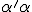
] + [

] + [
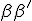
]
concording to the definition of the Sum,
And there
[
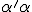
] = –[
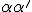
] = –[
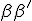
] exists
Thusly heaves up themselves [
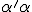
] and [
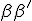
] by considering the Addition, and it is really by working through
[
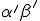
] = [

]
Footnotes
•This besigning of the line segment is Only for a forward runnining line segment. The enduring besigning of the same through its boundong elements can firstly become everyway standing, if we the knitting of the elements have learned to Recognise to be( see the second section § 99)
The besigning [

] is chosen in the Ausdehnungslehre from 1862 for the product of both elements
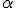
and

, which if [

and

are points, represents the
line part between

and

, whererom the line segment therethrough distinguishes itself, that in these ones only Length and direction, but in those ones at the same time, the position and unending-like, direct line comes to be held fixed, to which the line part is relating.
Therefore it is here around, thusly more therebesides, to firmly hold, that the besigning of the line segment through

only a forward running Aide is, the material measured besigning
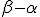
can concording to the principle of representing first in §99 com to be given. (1877)
•• above all, compare here §7














