|
cKleinhuis
|
 |
« on: December 17, 2009, 03:13:58 AM » |
|
i have entered the rather simple burning ship formula 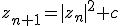 it is the burning buld fractal at 2 exponent ! front and rear view  rendered with pixelbender skript on gpu |
|
|
« Last Edit: December 17, 2009, 08:45:24 PM by Trifox »
|
Logged
|
---
divide and conquer - iterate and rule
|
|
|
|
kram1032
|
|
« Reply #1 on: December 17, 2009, 02:07:04 PM » |
|
looks way more interesting than the 2D-version  |
|
|
|
|
Logged
|
|
|
|
|
matsoljare
|
|
« Reply #2 on: December 17, 2009, 05:50:26 PM » |
|
The 2D burning ship is very interesting, when you start to zoom in on it...
|
|
|
|
|
Logged
|
|
|
|
bugman
Iterator
Posts: 122
|
|
« Reply #3 on: December 17, 2009, 06:14:17 PM » |
|
Very neat! I'm not clear what do you mean by abs(z)? For the complex case it should be: xnew+iynew = x²-y² + 2i|xy| - zc
|
|
|
|
« Last Edit: December 17, 2009, 06:17:09 PM by bugman »
|
Logged
|
|
|
|
|
kram1032
|
|
« Reply #4 on: December 17, 2009, 06:15:33 PM » |
|
abs z is clear. it's just the radius with phi=0° and theta=0° just compare polar coordinate complex abs  |
|
|
|
|
Logged
|
|
|
|
|
Fray
|
|
« Reply #5 on: December 17, 2009, 06:17:18 PM » |
|
what algebra is it?
i've got different results with quaternions:
z[n+1] = (abs(z.a) + abs(z.b)*i + abs(z.c)*j + abs(z.d)*k)^2 + h
|
|
|
|
Logged
|
"There is Plenty of Room at the Bottom"
|
|
|
bugman
Iterator
Posts: 122
|
|
« Reply #6 on: December 17, 2009, 06:19:50 PM » |
|
abs z is clear. it's just the radius with phi=0° and theta=0° just compare polar coordinate complex abs If so, then I don't think this is the correct formula for the Burning Ship, but it's still interesting. |
|
|
|
« Last Edit: December 17, 2009, 06:35:34 PM by bugman »
|
Logged
|
|
|
|
|
kram1032
|
|
« Reply #7 on: December 17, 2009, 06:46:08 PM » |
|
ah, wait, yeah, forgot... abs(real)+abs(imag) for complex... well... convert from spherical to cartesian and then abs(x) abs(y) abs(z)  |
|
|
|
|
Logged
|
|
|
|
|
cKleinhuis
|
|
« Reply #8 on: December 17, 2009, 08:44:46 PM » |
|
=|x|) and it is the same for more dimensions sorry for confusion i have corrected the above notation  @gaston3d the used algebra is polar coordinate triplex, d.white & p.nylanders version, as defined on: http://www.fractalforums.com/theory/triplex-algebra/i will go and try to find more simple base fractals, was experimenting with barnsley. until i understand how to modify the derivations for new functions i will wait for trying newtonian, or diverging fractals it is very enjoying seeing that thing morph in realtime on my gts250 gpu, i really hope there will be a numbers library with arbitrary precision for gpus soon to work with greater precision  |
|
|
|
« Last Edit: December 17, 2009, 08:49:54 PM by Trifox »
|
Logged
|
---
divide and conquer - iterate and rule
|
|
|
|
BradC
|
|
« Reply #9 on: December 17, 2009, 08:47:32 PM » |
|
Do you mean |(x, y, z)| = (|x|, |y|, |z|) ?
|
|
|
|
|
Logged
|
|
|
|
|
cKleinhuis
|
|
« Reply #10 on: December 17, 2009, 08:50:11 PM » |
|
yes
|
|
|
|
|
Logged
|
---
divide and conquer - iterate and rule
|
|
|
|
Fray
|
|
« Reply #11 on: December 17, 2009, 09:10:16 PM » |
|
i think formula z[n+1] = |z[n]|^2 + c is still improper and is equivalent to z[n+1] = z[n]^2 + c
one of definitions of absolute value is: abs(a+bi+...) = sqrt(a^2+b^2+...), then (abs(z))^2 = z^2
|
|
|
|
|
Logged
|
"There is Plenty of Room at the Bottom"
|
|
|
|
Fray
|
|
« Reply #12 on: December 17, 2009, 09:28:42 PM » |
|
... i really hope there will be a numbers library with arbitrary precision for gpus soon to work with greater precision ...
i am not into gpu programing, but read somewhere that 64 bit double precision were introduced in shader model 5 (directx11) and is supported by nvidia gt200 chipset |
|
|
|
|
Logged
|
"There is Plenty of Room at the Bottom"
|
|
|
bugman
Iterator
Posts: 122
|
|
« Reply #13 on: December 17, 2009, 09:48:56 PM » |
|
Do you mean |(x, y, z)| = (|x|, |y|, |z|) ?
You might also want to try {|x|, |y|, z}, as that seems to give interesting results as well, and the cross section in the x-y plane still contains the 2D Burning Ship fractal. |
|
|
|
|
Logged
|
|
|
|
|
cKleinhuis
|
|
« Reply #14 on: December 17, 2009, 10:15:07 PM » |
|
Do you mean |(x, y, z)| = (|x|, |y|, |z|) ?
You might also want to try {|x|, |y|, z}, as that seems to give interesting results as well, and the cross section in the x-y plane still contains the 2D Burning Ship fractal. yes, that is what i did, i think it is nice to have possible 3d analogons of existing fractals using the triplex algebra, i am right now into trying several formulas, which do not need additional functions ( sin,cos ... ) btw. having the original 2d complex numbers fractal in one plane is a must ... |
|
|
|
|
Logged
|
---
divide and conquer - iterate and rule
|
|
|
|
November 29, 2010, 10:13:29 AM
Burning Fleet
3d Art / Composition
Dilber MC Theme by HarzeM