MathJason
Forums Newbie

Posts: 9
|
 |
« on: September 16, 2016, 02:40:49 AM » |
|
Between any two points in the Mandelbrot set, there is a continuous path. (Well...this isn't a theorem yet, but it is very likely true.) Moreover, this path is basically unique. (Formally, there is one unique set of Misiurewicz points and hyperbolic components that any such path would go through without self intersecting. Again, not a theorem that I know of, but very probably true.) Anyone who has seen a high-quality zoom of the Mandelbrot set has seen the thin filaments connecting the big M-brot to the minibrots. - Can we write a program which would practically draw the path connecting any two given points in the Mandelbrot set?
- Has such a program already been written?
- Are there images or videos online of this?
My guess on how to implement it is to construct the M-set using distance estimation and then to just search for the path using a path-finding algorithm. Of course if the resolution is not good enough, it might find false paths. I imagine the center of spirals may give it trouble as well as connecting a point outside a minibrot to the minibrot itself (such as the path connecting 0+0i to a minibrot which goes through the cusp of the minibrot cardioid). Motivation: I think it would be cool to see the path though a Julia island that starts at the edge (where it connects to 0+0i) and travels to the center. More so, every zoom (especially one ending at a minibrot) just traces a complex winding path through the the M-set. It would be fun to see such a path highlighted in a zoom video. (Or better yet, to avoid giving away where the zoom is headed, one could have the path dynamically drawn using a glowing dot which traces a trail behind it. Like Tinkerbell in the Disney movies. Maybe, like Tinkerbell, it could also light-up each hyperbolic component as it passes through it.  ) |
|
|
|
|
 Logged
Logged
|
|
|
|
|
TheRedshiftRider
|
 |
« Reply #1 on: September 16, 2016, 06:16:14 AM » |
|
|
|
|
|
|
 Logged
Logged
|
Motivation is like a salt, once it has been dissolved it can react with things it comes into contact with to form something interesting.  |
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #2 on: September 16, 2016, 01:21:57 PM » |
|
The trouble is that passing through even 1 Misiurewicz point is in general an infinite spiral, so you need to pick an arbitrary resolution to know when to stop spiralling in and switch to spiralling out. And if you pass through one Misiurewicz point you'll pass through an infinity of them (and an infinity of minibrots too). Your idea of drawing using distance estimation at a particular resolution then analyzing the image is probably as good as it will get, maybe some kind of adaptive resolution increase when you're in doubt over which way to go could maybe help too, though it's hard to know when to stop (and the boundary has dimension 2, so it's quite hairy). But you may be interested in "Internal addresses in the Mandelbrot set and Galois groups of polynomials" Dierk Schleicher http://arxiv.org/abs/math/9411238 which describes angled internal addresses which identify hyperbolic components in a path-like way by saying which other hyperbolic components you have to pass through to reach them. In particular it describes a conceptual "long address" which lists the whole infinity of components on the route (the regular addresses are strictly increasing in mentioned periods). Lighting up hyperbolic components is comparatively easy. First step is to find the period and nucleus, then trace points along the boundary using Newton's method. Example output: https://mathr.co.uk/mandelbrot/2012-11-02_boundary_trace.svg |
|
|
|
|
 Logged
Logged
|
|
|
|
MathJason
Forums Newbie

Posts: 9
|
 |
« Reply #3 on: September 16, 2016, 08:44:13 PM » |
|
Claude, I'm not sure that Misiurewicz points will be a huge problem since at a fairly good resolution, one will be able to separate the arms of the spiral except near the center. However, I think minibrots will be a challenge since they are often surrounded by a dense halo of filaments.
Either way, it seems I should just try to code up something simple and see how it goes.
The internal address stuff is cool and I may look into it more, but this is beyond anything I want to think about right now. Although, it would certainly provide a nice solution to this problem if one could efficiently locate the largest hyperbolic component between any two given hyperbolic components.
|
|
|
|
|
 Logged
Logged
|
|
|
|
bkercso
Fractal Lover
 
Posts: 220
|
 |
« Reply #4 on: October 06, 2016, 01:04:41 PM » |
|
If I would want to solve the problem by analizing a picture, I would play with max. iteration number adaptively, rather than the image resolution. Lower iteration numbers gives you thicker filaments.  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
|
Adam Majewski
|
 |
« Reply #6 on: October 06, 2016, 03:52:57 PM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Adam Majewski
|
 |
« Reply #7 on: October 06, 2016, 04:11:04 PM » |
|
@Claude
Can you describe method for drawing internal rays ?
|
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #8 on: October 06, 2016, 07:53:26 PM » |
|
The first couple of paragraphs here explain the problem as a pair of equations that can be solved using Newton's method in two complex variables: https://mathr.co.uk/blog/2013-04-01_interior_coordinates_in_the_mandelbrot_set.htmlYou need to know the period of the component, and you can start from the nucleus with b = 0 and gradually increase r to 1 in b = r e^(i theta) where theta is the internal angle of the ray you want to trace. Be careful when theta is 0 and the component is not a cardioid, as it can become unstable when r gets close to 1 and jump out of the child component to find the root of the parent component... Here's some C99 code that implements it (the 2x2 complex matrix inversion is inlined somewhat): #include <complex.h>
#include <math.h>
static inline double cabs2(double _Complex z) {
return creal(z) * creal(z) + cimag(z) * cimag(z);
}
static inline bool cisfinite(double _Complex z) {
return isfinite(creal(z)) && isfinite(cimag(z));
}
static const double epsilon2 = 1.9721522630525295e-31;
enum m_newton { m_failed, m_stepped, m_converged };
typedef enum m_newton m_newton;
extern m_newton m_d_interior_step(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period) {
double _Complex c = c_guess;
double _Complex z = z_guess;
double _Complex dz = 1;
double _Complex dc = 0;
double _Complex dzdz = 0;
double _Complex dcdz = 0;
for (int p = 0; p < period; ++p) {
dcdz = 2 * (z * dcdz + dc * dz);
dzdz = 2 * (z * dzdz + dz * dz);
dc = 2 * z * dc + 1;
dz = 2 * z * dz;
z = z * z + c;
}
double _Complex det = (dz - 1) * dcdz - dc * dzdz;
double _Complex z_new = z_guess - (dcdz * (z - z_guess) - dc * (dz - interior)) / det;
double _Complex c_new = c_guess - ((dz - 1) * (dz - interior) - dzdz * (z - z_guess)) / det;
if (cisfinite(z_new) && cisfinite(c_new)) {
*z_out = z_new;
*c_out = c_new;
if (cabs2(z_new - z_guess) <= epsilon2 && cabs2(c_new - c_guess) <= epsilon2) {
return m_converged;
} else {
return m_stepped;
}
} else {
*z_out = z_guess;
*c_out = c_guess;
return m_failed;
}
}
extern m_newton m_d_interior(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period, int maxsteps) {
m_newton result = m_failed;
double _Complex z = z_guess;
double _Complex c = c_guess;
for (int i = 0; i < maxsteps; ++i) {
if (m_stepped != (result = m_d_interior_step(&z, &c, z, c, interior, period))) {
break;
}
}
*z_out = z;
*c_out = c;
return result;
} or from my mandelbrot-numerics repository: https://code.mathr.co.uk/mandelbrot-numerics/blob/HEAD:/c/lib/m_d_interior.cThe idea when tracing an internal ray is to call m_d_interior with the previous z, c outputs as z, c guesses, while increasing the radius of the argument interior = radius * cexp(I * twopi * angle). maxsteps around 16 should easily be enough. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Adam Majewski
|
 |
« Reply #9 on: October 06, 2016, 09:14:24 PM » |
|
Here is what I have done /*
drawing internal ray by Claude Heiland-Allen
http://www.fractalforums.com/mandelbrot-and-julia-set/pathfinding-in-the-mandelbrot-set/?topicseen
Here's some C99 code that implements it (the 2x2 complex matrix inversion is inlined somewhat):
gcc i.c -Wall -lm
*/
#include <stdbool.h> // bool
#include <complex.h>
#include <math.h>
static inline double cabs2(double _Complex z) {
return creal(z) * creal(z) + cimag(z) * cimag(z);
}
static inline bool cisfinite(double _Complex z) {
return isfinite(creal(z)) && isfinite(cimag(z));
}
static const double epsilon2 = 1.9721522630525295e-31;
//
enum m_newton { m_failed, m_stepped, m_converged };
typedef enum m_newton m_newton;
extern m_newton m_d_interior_step(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period) {
double _Complex c = c_guess;
double _Complex z = z_guess;
double _Complex dz = 1;
double _Complex dc = 0;
double _Complex dzdz = 0;
double _Complex dcdz = 0;
for (int p = 0; p < period; ++p) {
dcdz = 2 * (z * dcdz + dc * dz);
dzdz = 2 * (z * dzdz + dz * dz);
dc = 2 * z * dc + 1;
dz = 2 * z * dz;
z = z * z + c; // fc(z) = z^2 + c
}
double _Complex det = (dz - 1) * dcdz - dc * dzdz;
double _Complex z_new = z_guess - (dcdz * (z - z_guess) - dc * (dz - interior)) / det;
double _Complex c_new = c_guess - ((dz - 1) * (dz - interior) - dzdz * (z - z_guess)) / det;
if (cisfinite(z_new) && cisfinite(c_new)) {
*z_out = z_new;
*c_out = c_new;
if (cabs2(z_new - z_guess) <= epsilon2 && cabs2(c_new - c_guess) <= epsilon2) {
return m_converged;
} else {
return m_stepped;
}
} else {
*z_out = z_guess;
*c_out = c_guess;
return m_failed;
}
}
extern m_newton m_d_interior(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period, int maxsteps) {
m_newton result = m_failed;
double _Complex z = z_guess;
double _Complex c = c_guess;
for (int i = 0; i < maxsteps; ++i) {
if (m_stepped != (result = m_d_interior_step(&z, &c, z, c, interior, period))) {
break;
}
}
*z_out = z;
*c_out = c;
return result;
}
/*
You need to know the period of the component,
and you can start from the nucleus with b = 0
and gradually increase r to 1 in
b = r e^(i theta)
where theta is the internal angle of the ray you want to trace.
Be careful when theta is 0 and the component is not a cardioid,
as it can become unstable when r gets close to 1 and jump out of the child component to find the root of the parent component...
The idea when tracing an internal ray is to
call m_d_interior with the previous z, c outputs as z, c guesses,
while increasing the radius of the argument interior = radius * cexp(I * twopi * angle).
maxsteps around 16 should easily be enough.
draw_internal_ray( 1, 0, "1/2", 16);
*/
void draw_internal_ray(int period, double _Complex nucleus, const char *angle) {
int maxsteps = 16;
????
}
int main (void) {
double _Complex nucleus;
int period=1;
return 0;
}
|
|
|
|
|
 Logged
Logged
|
|
|
|
MathJason
Forums Newbie

Posts: 9
|
 |
« Reply #10 on: October 07, 2016, 03:00:58 AM » |
|
Since this thread is revived, I thought I'd share what I've done. I generated a portion of the Mandelbrot set and then used Dykstra's algorithm to find the "shortest path" though that image. (Technically, I used some complicated edge weight between adjacent pixels based on the distance estimation method. The idea is that pixels with a distance closer to 0 are preferable, and consecutive pixels both with a bad distance are to be avoided at all costs.) The results (see below) are interesting, but not close to accurate. You can see that with better resolution, the path gets better. Some adaptive increase in resolution (or just a much larger resolution image) would certainly help in finding a more accurate path. The two +'s represent the endpoints of the path that I fed the algorithm. (The location is -1.770119403587, 0.0041109401046462)  http://sta.sh/0nemzelf6lq http://sta.sh/0nemzelf6lq http://sta.sh/019ug0o4hf9c http://sta.sh/019ug0o4hf9c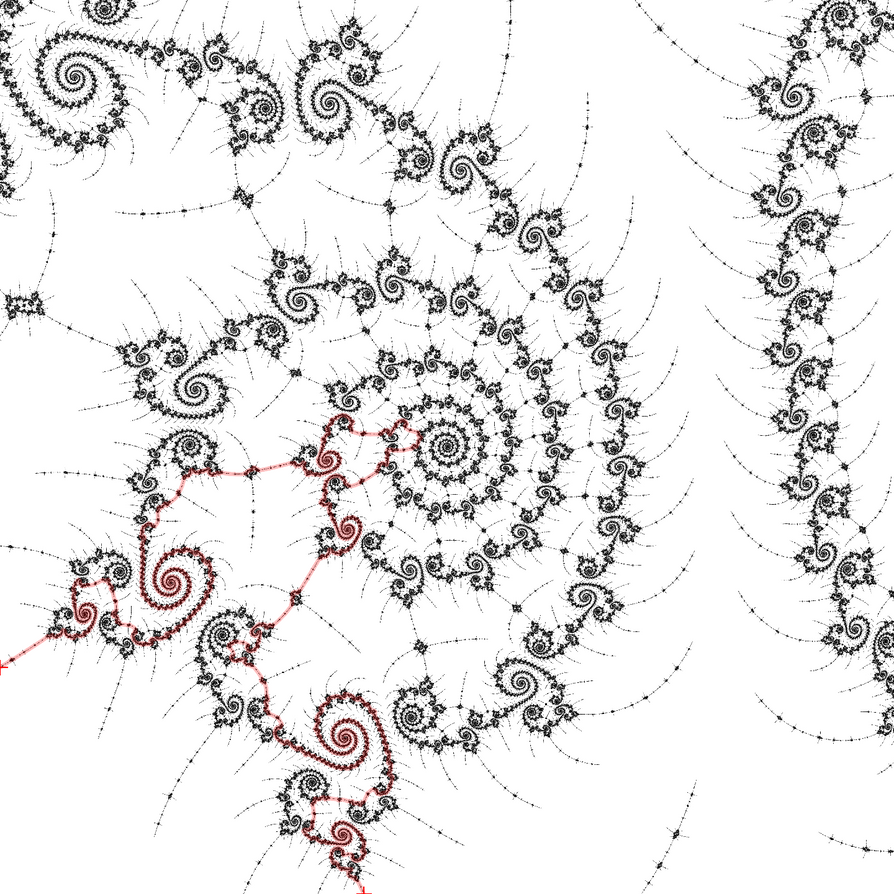 http://sta.sh/0v1kgnby7xb http://sta.sh/0v1kgnby7xbYou can tell the algorithm is particularly bad with Misiurewicz points at the center of single spirals. It should be going to the center of the spiral using the thin filaments. The spiral itself is not connected along the "spiral part"---it just looks that way (to both the computer and the human eye). Also, while the generated path does go to the center of the double spirals, it doesn't go along the correct path. It should take the inside path (again via thin filaments that are barely visible.) I have to admit however, that the algorithm is probably better than my human eyes at identifying the path. (Of course my human intellect is better than both the computer and my eyes, being able to deduce the correct pattern.) |
|
|
|
« Last Edit: October 07, 2016, 03:22:04 AM by MathJason »
|
 Logged
Logged
|
|
|
|
MathJason
Forums Newbie

Posts: 9
|
 |
« Reply #11 on: October 07, 2016, 03:13:03 AM » |
|
Also, on a different note, it seems that it would help greatly to know the values of certain important points on the path. This leads to two related but different questions: - Is it known how to compute the external address of the largest mini-mandelbrot and/or Misiurewicz point between two other external angles? I am sure this is related that the "long addresses" that Claude mentioned.
- Given a rational external angle (in a discrete representation such as 1/3 or .(01)), how easy is it to compute the point on the Mandelbrot set boundary associated with that angle? I noticed Claude's online tool, http://mathr.co.uk/mandelbrot/web/, doesn't compute this information, which makes me believe it is difficult.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
|
Adam Majewski
|
 |
« Reply #13 on: October 07, 2016, 08:43:40 AM » |
|
is it known how to compute the external address of the largest mini-mandelbrot and/or Misiurewicz point between two other external angles? I am sure this is related that the "long addresses" that Claude mentioned.[/li][/list]
* Principal Misiurewicz point , principal spoke of the limb * characteristic Misiurewicz point : http://www.tic.itefi.csic.es/gerardo/publica/Romera96b.pdf |
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #14 on: October 07, 2016, 03:29:43 PM » |
|
Here is what I have done
Maybe this is of interest: https://code.mathr.co.uk/mandelbrot-graphics/blob/HEAD:/c/bin/m-subwake-diagram-a.c#l25Also, on a different note, it seems that it would help greatly to know the values of certain important points on the path. This leads to two related but different questions: - Is it known how to compute the external address of the largest mini-mandelbrot and/or Misiurewicz point between two other external angles? I am sure this is related that the "long addresses" that Claude mentioned.
- Given a rational external angle (in a discrete representation such as 1/3 or .(01)), how easy is it to compute the point on the Mandelbrot set boundary associated with that angle? I noticed Claude's online tool, http://mathr.co.uk/mandelbrot/web/, doesn't compute this information, which makes me believe it is difficult.
Computations with external angles are easiest when expressed in binary. For example, the largest periodic angle between .(01) and .(011) is .(0110), which is less than the upper angle .011011011... and greater than the lower angle..010101010... There is probably an algorithm to determine the angle directly, perhaps some experimentation with different concrete examples would give some hints how to derive it. The problem of determining the point on the boundary associated with an external angle can be solved partially by "tracing external rays". It's not entirely trivial, but it's certainly possible - I have code to do it, but I haven't ported it to the web-based tool (which mostly contains symbolic algorithms, not numerical ones). See the code here: https://code.mathr.co.uk/mandelbrot-numerics/blob/HEAD:/c/lib/m_d_exray_in.c (double precision) https://code.mathr.co.uk/mandelbrot-numerics/blob/HEAD:/c/lib/m_r_exray_in.c (arbitrary precision). For explanation, http://www.math.titech.ac.jp/~kawahira/programs/mandel-exray.pdfThe rays get closer and closer to the boundary, but don't reach it in finite time - for a more exact boundary point you need to switch to different methods when the ray is close enough. For points on the boundary of hyperbolic components, split the internal angled address (computable from the angle) into island and child path components, when tracing the ray to the parent island use atom domain test (to see if Newton's method is likely to converge to the right place) and switch to Newton's method to find the nucleus of the parent island and then trace internal rays through the chain of connected components to the desired boundary point. For Misiurewicz points, there is probably a similar test to the atom domain test after which point Newton's method will converge to the desired location (though rays to Misiurewicz points tend to converge much more quickly than rays to roots of hyperbolic components anyway). The atom domain test checks that the iteration count of the last minimum of |z| is the same as the period of the ray. |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















