The All New FractalForums is now in Public Beta Testing! Visit FractalForums.org and check it out!
|
|
|
||||||
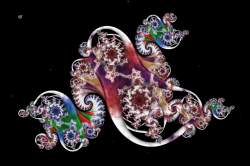
| Medusa | ||||||
| Previous Image | Next Image | ||||||
| Description: A Kleinian Group fractal based on methods described in the excellent book "Indra's Pearls - The Vision of Felix Klein" by David Mumford, Caroline Series, and David Wright. Created with the Fractal Science Kit. Key Links: Main page: http://www.fractalsciencekit.com/index.htm Fractal Gallery: http://www.fractalsciencekit.com/gallery/gallery.htm Fractal Tutorials: http://www.fractalsciencekit.com/tutorial/intro.htm Fractal Examples: http://www.fractalsciencekit.com/tutorial/examples/examples.htm Enjoy, Ross Hilbert hilbert@fractalsciencekit.com Stats: Total Favorities: 0 View Who Favorited Filesize: 293.24kB Height: 900 Width: 900 Keywords: Fractal Science Kit Orbit Trap Medusa Kleinian Group Indra's Pearls Posted by: Ross Hilbert  May 15, 2009, 07:39:53 PM May 15, 2009, 07:39:53 PMRating:      by 3 members. by 3 members.Image Linking Codes
|
||||||
| 0 Members and 1 Guest are viewing this picture. |
|
Comments (7)  |
|
| cKleinhuis | May 19, 2009, 09:38:06 PM hi there, just got the book "Indra's Pearls" what an excellent book! just browsing through the pages and i am enjoing the illustrations of the little man building different objects ( torus, moebius sphere  ) .... thx ) .... thxvery good and deep informations and many detailed description of the principles |
| Ross Hilbert | May 17, 2009, 06:44:40 PM Yes, you can create a Kleinian Group fractal as a strange attractor. Unlike an IFS which is generated from a set of affine transformations, a Kleinian Group fractal is generated from a pair of Mobius transformations and their inverse transformations. A Mobius transformation is similar to an affine transformation in that they both include rotation, translation, and scaling, but Mobius transformations do not support reflection in a line but do allow complex inversion (f(z) = 1/z) which is not supported by affine transformations. A Mobius transformation has the general form: f(z) = (A*z+B)/(C*z+D), where A, B, C, D, and z are complex numbers. See the book Indra's Pearls for further details. David Wright, one of the author's, also has a great web site at: http://klein.math.okstate.edu/IndrasPearls/. Ross |
| cKleinhuis | May 17, 2009, 10:02:21 AM i believe the kleinian group can be created like an ifs fractal ? you have a starting point ( on a circle ) and the transformations are mirroring, rotating, and the kleinian group is all the points that are reached before starting point is reached again ? so, i would try to render it as straightforward, so, setting a startpoint, apply the transformations and render a sphere on each of these points.... |
| Ross Hilbert | May 16, 2009, 04:40:28 PM Kleinian Group fractals are fractals. The implementation of the render in a specific fractal program is based on where it 'fits' in the program framework, of course. The Fractal Science Kit supports Kleinian Group fractals in 2 different ways; 1) as an orbit trap composed of tens of thousands of circles and 2) as a strange attractor. When using the orbit trap implementation, you would normally only display the 1st dwell to generate the image since the real work is done by the orbit trap. You can display other dwells or apply complex transformations but these will usually distort the shape of the circles. Using Mobius transformations to alter the base Kleinian Group fractal as is done in Medusa above will preserve the circles. I think you may have a little trouble rendering them in real-time given the complexity of the fractal but maybe your computer is much faster than mine :-) Ross |
| cKleinhuis | May 16, 2009, 04:03:40 PM hello, thank you for the tip, i want to render them in realtime, i will go and buy the book so it is a coloring algorithm not a fractal ? |
| Ross Hilbert | May 16, 2009, 01:58:29 PM The image was produced using the Kleinian Group orbit trap program that is part of the Fractal Science Kit fractal generator. The math/algorithms behind the program are described in the excellent book "Indra's Pearls - The Vision of Felix Klein" by David Mumford, Caroline Series, and David Wright. In fact, the whole book is dedicated to explaining how to produce pictures such as this. I highly recommend you get this book if you want to understand Kleinian Group fractals. If you are just interested in generating the fractals, the Fractal Science Kit fractal generator is one option. See the Kleinian Group example at http://www.fractalsciencekit.com/tutorial/examples/kleingp.htm for additional details. Ross |
| cKleinhuis | May 16, 2009, 10:19:51 AM great image! i am wondering how to render those kleinian groups, i just found a complex formula with four parameters ( a,b,c,d ) but i do not really know how to produce a kleinian image ... i want to do it in realtime  can you provide a howto? can you provide a howto? |
Powered by SMF Gallery Pro