The All New FractalForums is now in Public Beta Testing! Visit FractalForums.org and check it out!
|
|
|
||||||
| baroque | ||||||
| Previous Image | Next Image | ||||||
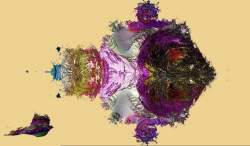
| Description: this picture is only a fragment of a large picture, i failed several times to upload it here. The complete picture should be available here(but as i found, again it is not completely available, but maybe it will give an impression of some spiralic features): http://trajektorulm.tr.funpic.de/index.htm made with an algorithm described at "more informations" on Youtube, video "artichoke"(the algo i wrote some years ago, it is implemented in QUASZ as gedatou(but only for power 2). the angles(measured from the northern pole and from meridian with geographic length zero) are multiplied with "power", as well as the distance of z1 is taken to the "power", the fragment of code goes as(the result is a trajectorial system just between the wonderful mandelbulb-algo and the squaring (or taking to higher powers) of quaternions: a1 = x1 * x1 + y1 * y1 + z1 * z1; //a2 = a1;//: REM new distance if squaring only a1 = sqrt(a1); loa1=log(a1); a2=exp(power*loa1); yioi1 = y1 * y1 + z1 * z1; yioi1 = sqrt(yioi1) ; //alpha1 = angle(x1, yioi1); alpha1 = arg(x1+1i* yioi1);(would be in C++ alpha1=atan2(x1,yioi1))// if not, then atan2(yioi1,x1) gamma1 = arg(y1+1i* z1); alpha2 = power*alpha1; gamma2 =power* gamma1 ; x2 = cos(alpha2) * a2 ; yioi2 = sin(alpha2) * a2 ; y2 = (yioi2) *cos(gamma2); z2 = (yioi2) * sin(gamma2) ; Stats: Total Favorities: 0 View Who Favorited Filesize: 206.54kB Height: 622 Width: 939 Keywords: mandelbulb mandelbrot set threedimensional fractals Posted by: vector  January 08, 2010, 05:50:51 PM January 08, 2010, 05:50:51 PMRating:     by 1 members. by 1 members.Image Linking Codes
|
||||||
| 0 Members and 1 Guest are viewing this picture. | ||||||
| Related Images | ||||||
|
|
Comments (0)  |
Powered by SMF Gallery Pro