|
Chris Thomasson
|
 |
« on: May 18, 2015, 12:23:25 AM » |
|
I need some help with converting a Julia set IFS that computes Julia fractals of the second power into one that works with higher powers. Basically, I have a Julia point C as a given, and a random point Z to work with. During iteration I take the distance D from Z to C, then the angle A and finally get a radius R by using the square root of D. I use a random number in the interval of [0...1] to create a probability factor F to help decide on which image I should use in R, a positive or negative. Then I take the cos/sin of the angle A divided by two. The result is then multiplied by the R selected with F. The resulting point is plotted, and used as the new Z in the next iteration.
This is working well for power of two Julia sets. However, I am having trouble converting this into a, perhaps, general form that can create Julia fractals for any given power...
Any help would be greatly appreciated!
Thanks.
:^)
|
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #1 on: May 18, 2015, 01:35:44 AM » |
|
So you have 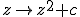 and you invert it to ^{1/2} \to z) , choosing one of the 2 roots at random. For an integer power 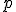 , the process is the same ^{1/p} \to z) with 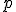 roots to choose from - luckily you are using polar form already, so you can take the positive real 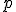 th root of D ( 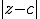 ) to give R, and divide the angle A by 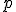 instead of 2. Now you can choose which of the complex roots to use, by adding an integer multiple (with the integer chosen at random from ![[0,1,...,p-1]](/cgi-bin/mimetex.cgi?[0,1,...,p-1]) ) of 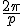 - take the 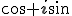 of this angle and multiply by R as before to give the new Z. This method still works for 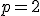 , because adding 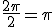 to an angle negates the result. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #3 on: May 18, 2015, 03:56:52 PM » |
|
Don't reinvent the wheel use Apo's plugins they are opensource and there is a juliaN and even phoenix julia  Also the complex pow julia was done at least twice already  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|
lycium
|
 |
« Reply #4 on: May 18, 2015, 04:58:57 PM » |
|
Apophysis' rendering is really bad, and I don't think its Julia or JuliaN are actually "correct" (in the sense of doing what is described above). The information given in this thread is pretty much exactly what is needed, no more no less  (I also recommend using the MIIM method with derivative if you need a really accurate visualisation.) |
|
|
|
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #5 on: May 18, 2015, 05:56:50 PM » |
|
Of course but still it gives a great starting point, just reading the plugin src code you haven't got to start from zero... I think.  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|
Chris Thomasson
|
 |
« Reply #6 on: May 18, 2015, 10:20:52 PM » |
|
So you have <Quoted Image Removed> and you invert it to <Quoted Image Removed>, choosing one of the 2 roots at random. For an integer power <Quoted Image Removed>, the process is the same <Quoted Image Removed> with <Quoted Image Removed> roots to choose from - luckily you are using polar form already, so you can take the positive real <Quoted Image Removed>th root of D (<Quoted Image Removed>) to give R, and divide the angle A by <Quoted Image Removed> instead of 2. Now you can choose which of the complex roots to use, by adding an integer multiple (with the integer chosen at random from <Quoted Image Removed>) of <Quoted Image Removed> - take the <Quoted Image Removed> of this angle and multiply by R as before to give the new Z. This method still works for <Quoted Image Removed>, because adding <Quoted Image Removed> to an angle negates the result.
Thank you so much for reading my query, and giving such a concise answer! Looking back through some experimental try's of mine wrt getting a general algorithm, I noticed that I was failing to choose the right number of roots for a given power! So, I was iterating a cubic, and only choosing two roots. Well, IMHO, that is rather embarrassing, but luckily your excellent answer helped me find the error of my ways. BTW, I am coding my own personal software for fractals. ;^o Anyway, I have it working like a charm now. I have to admit, the extra roots make finding a probability factor for converging a rendering that has detailed spirals more difficult... Thanks again Claude! :^D |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Chris Thomasson
|
 |
« Reply #7 on: May 18, 2015, 11:17:28 PM » |
|
Don't reinvent the wheel use Apo's plugins they are opensource and there is a juliaN and even phoenix julia  Also the complex pow julia was done at least twice already  I like to be creative, and I enjoy creating my own software. I definitely learn a lot from the process at hand. Heck, the learning process itself seems to be naturally fractal in and of itself. Humm... Anyway, Thank you DarkBeam for your excellent hard work, and more importantly, your passion for said creations: Algorithms, Coding galore! :^D |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Chris Thomasson
|
 |
« Reply #8 on: May 18, 2015, 11:19:20 PM » |
|
FWIW, here is an experimental attempt at something interesting wrt using fractional powers for the power of the Julia set P. Also, this contains more than one Julia point, and slightly different dimensions/powers for each one:  Thanks again Claude! |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Chris Thomasson
|
 |
« Reply #9 on: May 20, 2015, 01:52:17 AM » |
|
FWIW, here is a simple low-res test of a basic zoom wrt: https://plus.google.com/101799841244447089430/posts/RFXih818KCyThe "static" must be due to the fact that I am using random numbers to select what root to actually follow during iteration.
<a href="https://www.youtube.com/v/ljeN7dYNHhQ&rel=1&fs=1&hd=1" target="_blank">https://www.youtube.com/v/ljeN7dYNHhQ&rel=1&fs=1&hd=1</a> |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Chris Thomasson
|
 |
« Reply #10 on: May 20, 2015, 01:53:27 AM » |
|
Yes. Quite right Adam. I am currently experimenting with some of these excellent methods. Thanks! :^D |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Chris Thomasson
|
 |
« Reply #11 on: May 20, 2015, 02:54:06 AM » |
|
The "static" must be due to the fact that I am using random numbers to select what root to actually follow during iteration.
Humm... I am wondering if I could perhaps reduce some of the static by simply "resetting" the random number generator before each frame. |
|
|
|
|
 Logged
Logged
|
|
|
|
youhn
Fractal Molossus
 
Posts: 696
Shapes only exists in our heads.
|
 |
« Reply #12 on: May 20, 2015, 07:46:54 AM » |
|
I think you might need multi-scale perlin noise, with the scale of the graininess just a bit larger than the maximum pixel size. http://devmag.org.za/2009/04/25/perlin-noise/And then do NOT reset the noise, but keep it in line and scale with the fractal. |
|
|
|
|
 Logged
Logged
|
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #13 on: May 20, 2015, 11:39:53 AM » |
|
FYI: That link is incorrect. What's being described is "value noise" and not Perlin (gradient) noise. http://www.java-gaming.org/topics/noise-bandpassed-white/27071/view.htmlI haven't looked into how this method is working, but you might want to look at a sobol sequence...I put some java & c code somewhere. The idea here is to generate 2D (or nD) random-like point sets that uniformly cover the domain. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
|


















