Tglad
Fractal Molossus
 
Posts: 703

|
 |
« on: December 01, 2010, 01:21:37 AM » |
|
Hello everyone, I was thinking yesterday how it would be really awesome to start animating 3d fractals like the KIFS in a fractal way. Currently animations vary parameters smoothly, what should look impressive is if they move so that the large pieces move slowly and widely, and the small details move quickly over small distances. Just like how a tree's trunk sways slowly but the small leaves flap quickly. If a reflection plane on a KIFS is given by a planePosition and planeNormal, then the code would be: float time = 0
for each animation frame
{
for each x,y,z
{
float t = time;
vector v = (x,y,z);
for each iteration
{
vector pos = planePosition + planeNormal*sin(t)*sizeOfMotion;
v.reflectAroundPlane(pos, planeNormal);
v *= scaleFactor;
t *= scaleFactor;
}
}
time = time + timeStep; // timeStep gives speed of motion
} Jesse, Buddhi, Rrrola, would you be interested in trying this out? |
|
|
|
« Last Edit: December 01, 2010, 01:23:22 AM by Tglad »
|
 Logged
Logged
|
|
|
|
|
The Rev
Guest
|
 |
« Reply #1 on: December 01, 2010, 04:01:03 AM » |
|
This is a terrific idea. When I put together an animation, I have three dimensions (well, two actually) that are fractally generated, but the fourth is just how I choose to move the camera and/or fractal image around. It would be amazing to have four fractally generated dimensions, with movement being iterative in nature in line with the equation that generates the form.
The Rev
|
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #2 on: December 04, 2010, 12:25:32 AM » |
|
Is anyone interested in trying this out? I promise I'll make some cool videos with it  |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #3 on: February 09, 2011, 02:47:03 AM » |
|
I have made some videos to demonstrate these fractally animated fractals (or fractal animations), as opposed to animated fractals.
This is an animated fractal tree, animating the angle parameter on a sine wave:
<a href="http://vimeo.com/moogaloop.swf?clip_id=19726752&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19726752&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>
This is how animating fractals currently works in mandelbulber etc.
This is a fractally animated fractal tree:
<a href="http://vimeo.com/moogaloop.swf?clip_id=19726673&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19726673&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>
It gives a much more natural appearance of a tree blowing in the wind. This type of animation models nature better because it is fractal in time as well as space. The first video is not a fractal animation, because the speed of movement is smooth.
Also, the fractally animated tree looks complex and random, in fact is is not. The smaller branches oscillate quicker so move out of synch with the larger branches. It is in fact very simple and just result from scaling time in the recursion, not just size.
Here's one in 3d
<a href="http://vimeo.com/moogaloop.swf?clip_id=19733475&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19733475&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>
Maybe they should be called dynamic fractals, defined as time scaling equally to space each iteration.
Could look really nice on the kaleidoscopics, to make them into real dynamic fractals.
|
|
|
|
« Last Edit: February 09, 2011, 06:16:27 AM by Tglad »
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #4 on: February 10, 2011, 02:09:23 AM » |
|
Here's another dynamic fractal:
<a href="http://vimeo.com/moogaloop.swf?clip_id=19769856&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19769856&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>I suppose its a sort of growth pattern, reminds me of bubbles forming on the top of a boiling broth. It actually models nature pretty well if you think of each circle as a plant or animal being born, growing and then dying. The small plants/animals are very common and have a very short life cycle, like mushrooms or ants; the big plants/animals are much fewer and have a much longer life cycle, like oak trees or elephants. So this 'growth fractal' is kind of fundamental in nature I think. Like the previous dynamic tree, this fractal is not at all random, the chaotic look just comes from the fact that the variations in size make each bubble run at a different rate so they are not in synch. Just like the dynamic tree, if you zoom in on a small area and watch it in slow motion, it will be exactly the same as watching the whole fractal. (I classify this as a '2-form void cluster' here https://sites.google.com/site/simplextable/3-simplex, though I'm not certain if this is the best way to classify dynamic fractals). |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #5 on: February 11, 2011, 02:30:55 AM » |
|
and here's another example of a dynamic fractal that also exists in nature:
<a href="http://vimeo.com/moogaloop.swf?clip_id=19810243&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19810243&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>
A dynamic cluster.
Unlike the growth dynamic fractal, in this one no disks appear or disappear, so it remains a simple cluster, just a dynamic version.
The number of different dynamic fractals is probably huge, but its interesting because it seems relatively unexplored. I hope to make a few more examples.
(Note that dynamic fractals are not the same as a moving slice through a 4d fractal).
|
|
|
|
|
 Logged
Logged
|
|
|
|
hobold
Fractal Bachius

Posts: 573
|
 |
« Reply #6 on: February 11, 2011, 03:16:03 AM » |
|
The growing circles fractal is unique among the examples so far in that it is the only construction where the time axis is indeed interchangeable with the spatial axes. I'll try to explain this observation more clearly, so bear with me through what seems to be a detour.
Let's build a non-moving fractal in three spatial dimensions. Specifically, let's take infinitely many filled spheres, the sizes of which adhere to a fractal distribution (i.e. few large ones, more medium sized ones and yet more small ones). We dither these spheres throughout space, non-overlapping, with smaller spheres filling the gaps between larger spheres. Occasional void zones may exist, but these, too, are fractally distributed (i.e. few large gaps, but more smaller gaps and so on).
We now have a static sculpture of filled spheres in three dimensions.
Now choose one straight line through that sculpture of filled spheres. Move one point along that line at constant speed. Through the moving point, a cutting plane can be defined that is orthogonal to the straight trajectory of the moving point.
The cutting plane, when intersected with the three dimensional sculpture of static spheres, will display the growing circles fractal.
Another way to see this special quality of the growing circles fractal is the above construction backwards: take all animation frames and stack them on top of each other as slices of volume data. Some other examples will result in whipped cream, some in fractals with substantial directional bias, and only one example will result in an isotropic three dimensional fractal.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #7 on: February 11, 2011, 09:57:46 AM » |
|
Super! Terrific! Fantastic!  Glad i dropped by! In case nobody gets it, this is very important stuff!Its also way cool, too! |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
Kali
|
 |
« Reply #8 on: February 11, 2011, 02:29:28 PM » |
|
Tom, congratulations, another great finding.
So simple ideas, so great results... this is what I love from fractals.
(Also I think fractals are the answer to everything...
a sacred plant showed me this, and this is the reason why I'm here at this forum)
|
|
|
|
« Last Edit: February 11, 2011, 03:53:50 PM by Kali »
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #9 on: February 14, 2011, 05:56:39 AM » |
|
@hobold, you're describing a 3d cluster (or 3d fractals) viewed through a moving 2d slice, similar but not the same as the growth fractal. Moving slices can look interesting but they don't describe nature because time isn't a space dimension, it's separate. The dynamic fractals in this topic are still conformal, since we scale time by the same amount as distance.
The next one is tricky:
<a href="http://vimeo.com/moogaloop.swf?clip_id=19910961&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19910961&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>
I guess its fractal brownian motion, or a colliding cluster, like perhaps an asteroid belt. This is simulated, so unlike previous ones the small disk paths are not just the larger disk paths in fast forward. However, I think you could actually make this as a recursively used path, but the path would be non-repeating and infinitely detailed, as such it is probably provable that any simulation like the video equates to an equivalent using recursive paths. So this video is really no different to the previous dynamic fractals.
I classify it as a 2-form cluster tree, because it takes on 2 forms. Firstly a cluster, but also trees are built up and dismantled at every collision, as seen circled. These trees are fractal/infinite because as you look at smaller disks the likelihood of one touching the disk in question increases to 1, so there must be a finite touching child disk, and therefore a grandchild disk and so on.
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #10 on: February 14, 2011, 02:16:13 PM » |
|
Not even the greatest scientist or philosophers can describe exactly what really time is, so I wouldn't say for sure that it is a definite separated non-spatial dimension. Sorry about the off-topic, but check this out: http://en.wikipedia.org/wiki/Eternalism_%28philosophy_of_time%29 |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #11 on: February 15, 2011, 12:06:05 AM » |
|
Indeed and thanks for the link. Here's another dynamic fractal, its like a tree blowing in the wind strong enough that the branches bang together. Hard to replicate so this is a simple version:
<a href="http://vimeo.com/moogaloop.swf?clip_id=19879237&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=19879237&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>It's a tree structure, but the collisions form and unform sponge fractals, as circled in red. 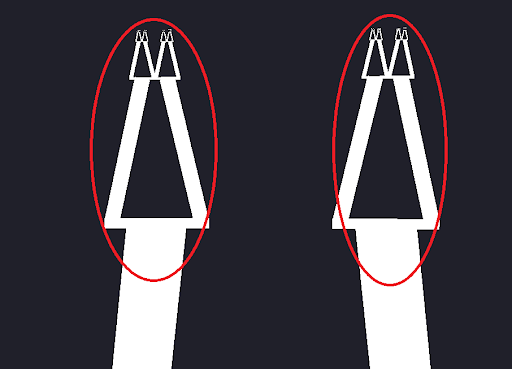   Maybe there are some more I can make but not sure. In the meantime here are three questions: 1. In all of these videos, how does the speed of the small parts compare to that of the large parts? Ignoring the first videos on waving trees: 2. How does the fractal 'self-connectivity' change from the first to the most recent videos? 3. Which is the odd one out? |
|
|
|
« Last Edit: February 15, 2011, 12:08:56 AM by Tglad »
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #12 on: February 16, 2011, 12:38:34 AM » |
|
I don't see self-conectivity in the fractals of growing bubbles, neither in the orbits one.
|
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #13 on: February 19, 2011, 12:28:21 AM » |
|
A simpler dynamic fractal is a sierpinski triangle rotating-
<a href="http://vimeo.com/moogaloop.swf?clip_id=20120900&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA" target="_blank">http://vimeo.com/moogaloop.swf?clip_id=20120900&amp;server=vimeo.com&amp;fullscreen=1&amp;show_title=1&amp;show_byline=1&amp;show_portrait=0&amp;color=01AAEA</a>
As you can see, mostly it is a void cluster (like 2d cantor dust is), but you can see it often becomes a void sponge, or void sponges, as in the pictures below.
The deeper you look, the more frequently these sponges occur, so you can't describe the whole fractal as just swapping from one type to another, the two are completely interwoven.
@kali... what about being connected to its later or previous self?
|
|
|
|
 Logged
Logged
|
|
|
|
|
Kali
|
 |
« Reply #14 on: February 19, 2011, 02:37:12 AM » |
|
@kali... what about being connected to its later or previous self?
Good point, but I find a little contradictory that you are pointing at that, after rejecting hobold's idea. It's pretty much the same. A 3D fractal made of stacking the 2D slices of each frame in the animation, is the best way to see this self-connectivity you are talking about, don't you think? (temporal connectivity also suggest the idea of time being a spatial dimension) By the way, liked the Sierpinski dynamic fractal. Good work. One thing that has me thinking about the last dynamic fractals: As each self similar part of the fractal get's smaller, does it really moves faster? As for the tree-like, the branches oscilates faster, but the distance between them it's smaller, so maybe the absolute speed of the edges of any branch it's the same? (or at least for the calculated median speed after a certain period of time, because they don't move at a constant speed) Also, in the Sierpinsky dynafractal, the smaller parts rotates at a faster rate, but as the radius is also smaller, maybe all the vertices have the same speed? I was also thinking what happens as we aproach infinity... infinite small parts oscilating or rotating at an infinite rate... It reminds me of something I read about string theory but I don't remember well what it was, I'll try to find it... |
|
|
|
« Last Edit: February 19, 2011, 05:07:35 AM by Kali »
|
 Logged
Logged
|
|
|
|
|


















