|
David Makin
|
 |
« Reply #15 on: August 14, 2014, 11:13:54 PM » |
|
Yes, PI is a fractal, maybe you just don't have the right visualisation.
I disagree - the digits of Pi are *chaotic* and anything *chaotic* can be converted into a fractal via appropriate manipulation - that does not make the original chaos itself "fractal" - for instance any general chaotic random generator (including a truly "real-world" random generator) can be used to produce say fBm fractals but that does not mean that the random sequence or sequences used can be said to be fractal themselves. The digits of Pi itself in the raw do not exhibit any self-similarity nor do they even resolve to a strange attractor (at least not as far as we know, one would literally have to check the full infinite digits to be certain). Also since I've often said "everything is fractal" I should clarify - the above is using the standard definition of a fractal - my own definition is simpler and more generic - a fractal is anything that can be produced using math that also produces fractals - this means effectively *all math* is a subset of fractal math and I seriously believe that is the way math (and indeed effectively all science) should be approached in future. |
|
|
|
« Last Edit: August 14, 2014, 11:19:46 PM by David Makin »
|
 Logged
Logged
|
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #16 on: August 15, 2014, 10:15:42 AM » |
|
Any pi=a/b expression is a circular argument. a and/or b must already contain pi.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
lkmitch
Fractal Lover
 
Posts: 238
|
 |
« Reply #18 on: August 15, 2014, 06:53:23 PM » |
|
I have to precise that what I was talking about is NOT random walks.
It's an algorithm in which the direction of the walk is linked to a property of the number and works for others constants than PI. The images reveals the true nature of such complicated numbers.
It has been applied to sqrt(n), e, ln(2), catalan number, etc... and produce really interesting fractals patterns.
As was said, it depends on what one means by random. The figures in my blog posting were created using the digits of pi, not with random numbers. It's called a random walk only because it appears random. |
|
|
|
|
 Logged
Logged
|
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #19 on: August 15, 2014, 08:54:26 PM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
hermann
Iterator

Posts: 181

|
 |
« Reply #20 on: August 23, 2014, 10:40:38 AM » |
|
The digits of 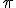 are random and no pattern has been discovered until know. So one of the main features of a fractal, self similarity of patters on different scales, is missing. On the other hand very interesting algorithems have been discovered to calculate 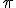 The following approximation algorithem shows a nice pattern:  By the way: The following aproximation can be used for 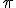 : 21053343141/6701487259 A comparable problem I am personal interested in are prime numbers. Which seems to appear random and patterns are hard to find. It seems to me that prime numbers are the non periodic part of the natural numbers. I have produced a lot of tables to visualise the distribution of prime numbers on my home page. I have used a lot of JavaScript for the calculation of the tables which challenges the numerical skills of a browser. I propose to use the firefox browser (That the one I used for the development). On windows 8.1 the explorer warns that he might crash but survives. With other Browsers I have no experience. http://www.wackerart.de/mathematik/primzahlen.htmlhttp://www.wackerart.de/mathematik/primzahlen_mountain.htmlThe only pattern i can visualy recognise are in the visualisation as Ulam Spriral. http://www.wackerart.de/mathematik/distribution_pattern.htmlAlso Gilbreath's Conjecture produces interesting patterns: http://www.wackerart.de/mathematik/gilbreaths_conjecture.htmlWhen someone is interested in prime numbers we may open a further thread? Hermann |
|
|
|
« Last Edit: August 23, 2014, 10:53:41 AM by hermann »
|
 Logged
Logged
|
|
|
|
|
TheRedshiftRider
|
 |
« Reply #21 on: August 31, 2014, 11:04:34 AM » |
|
I think PI would be more like a random fractal. C10 would be a better example.
|
|
|
|
|
 Logged
Logged
|
Motivation is like a salt, once it has been dissolved it can react with things it comes into contact with to form something interesting.  |
|
|
|
jehovajah
|
 |
« Reply #22 on: September 02, 2014, 12:35:36 PM » |
|
I figured you'd need additional digits to get additional precision, but it still strikes me as excessively weird that a known circumference and a known diameter require such extravagant methods to derive "true" values for pi.
Makes me question the whole idea really.
It is mathematically sound, but philosophically unacceptable to me.
Good thing I don't write the rulebooks for this stuff!
I am very sympathetic to your view Sockratease. Philosophically Kant used this situation to justify mathematics as a discoursive subject, one revealed to man by a transcendental being, hence pi was declared a transcendental number. The principle of exhaustion applies to pi, and that is another philosophical principle. Pragmatically Archimedes advised commenurability as the important or relevant outcome. When you move to the Indian Sages the taste for infinite exhaustive calculations as an end in themselves really gets introduced into the consciousness of mathematicians. Shunya being everything is experienced in these practices.the great circles of the years and epochs reflects their completely different but consistent approach to Shunya founded on the circular and spherical vortices of space. Reducing the count modulo 10 and modulo 9 revealed an incredible fractal structure which they represented spatially by a system of gears or clocks .this great fractal metronome we reduce to the decimal system, and in that system pi has a representation as an endless polynomial. The physical " polynomial" is a set of circular dials frozen at each sector representing the numerals of pi. This endless Arithmos sits within all possible Arithmoi described in this way, and each one can be geometrically arranged in space in any pattern which may itself be a fractal pattern or an endless tessellation. In the end the pursuit of numerals obscures the richer Spaciometry from which they may be drawn. The beauty of fractals for me is not the numeric processes used to generate them, but the algorithms used to generate surface plots and colours which depict extensive properties in space. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
Sockratease
|
 |
« Reply #23 on: September 02, 2014, 11:13:50 PM » |
|
I am very sympathetic to your view Sockratease.
Philosophically Kant used this situation to justify mathematics as a discoursive subject, one revealed to man by a transcendental being, hence pi was declared a transcendental number... Kant? Really? Wow. I always admired his Logic and am a bit surprised he took that position. It seems out of place with what I recall from the rest of his stuff {but my Philosophy courses were as long ago as my math and programming courses, so my memory may well be at fault!}. It's always fascinated me that when confronted by concepts like infinity so many otherwise rational thinkers fall back on metaphysics to explain things. But I guess it's an easy way out and it explains things with no further need for questions or elaborations, so it must be very tempting  |
|
|
|
« Last Edit: September 02, 2014, 11:15:45 PM by Sockratease, Reason: Grammatically Incorrect »
|
 Logged
Logged
|
Life is complex - It has real and imaginary components. The All New Fractal Forums is now in Public Beta Testing! Visit FractalForums.org and check it out! |
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #24 on: September 03, 2014, 04:40:18 AM » |
|
Pi itself is not the same as the decimal sequence of Pi. Pi itself is not chaotic, nor fractal nor random, it is just a real value.
If pi written in something other than base 10 were just 1.12345678.... we wouldn't think of it as a mysterious or interesting number would we?
That is what Roquen pointed out, if, instead of using a decimal sequence, we write pi as a sequence a.bcdefg... which is twice a + 1/(1/b + 1/(1/c + (1/(1/d + ....)))) then Pi is in fact 1.12345678...
|
|
|
|
|
 Logged
Logged
|
|
|
|
fractower
Iterator

Posts: 173
|
 |
« Reply #25 on: September 03, 2014, 05:34:04 AM » |
|
Interesting point Tglad.
Pi in base Pi is 10.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Sockratease
|
 |
« Reply #26 on: September 03, 2014, 06:14:59 PM » |
|
Pi itself is not the same as the decimal sequence of Pi. Pi itself is not chaotic, nor fractal nor random, it is just a real value.
If pi written in something other than base 10 were just 1.12345678.... we wouldn't think of it as a mysterious or interesting number would we?
That is what Roquen pointed out, if, instead of using a decimal sequence, we write pi as a sequence a.bcdefg... which is twice a + 1/(1/b + 1/(1/c + (1/(1/d + ....)))) then Pi is in fact 1.12345678...
Interesting point Tglad.
Pi in base Pi is 10.
Pi isn't interesting for the sequence of numerals, it is interesting for the special and extremely useful geometry it represents. Because of this special nature, it gets much more attention than other irrational numbers. Personally, I find e gives much more interesting results when plugged into various properties of fractal generators than pi (I like plugging mathematical constants in various places just to see what happens  |
|
|
|
|
 Logged
Logged
|
Life is complex - It has real and imaginary components. The All New Fractal Forums is now in Public Beta Testing! Visit FractalForums.org and check it out! |
|
|
lkmitch
Fractal Lover
 
Posts: 238
|
 |
« Reply #27 on: September 04, 2014, 05:49:00 PM » |
|
Pi isn't interesting for the sequence of numerals, it is interesting for the special and extremely useful geometry it represents.
I would say, pi isn't interesting *just* for the sequence of numerals... Quite a bit of effort has be spent computing zillions of digits of pi in base 10, when the value of the number (for practical purposes) has been known for a very long time. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #28 on: September 05, 2014, 02:26:20 AM » |
|
The ratio of a circular perimeter to a rectilineal diameter is given the label 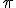 The ratio of a semi circular perimeter to that diameter is 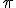 /2. A quarter circular arc to a radius is 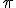 /2. The ratio of a circular disc to a square that sits between the radii of a quarter sector is 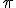 . 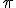 is not an Arithmos . It is a logos. Is a logos fractal? I do not think it can be any other. Euler used the notion of Equivalence classes to deal with the endless iterations involved with logoi. We are taught to " reduce" the endless fractal nature of ratios to their simplest form, because all logoi say too much! |
|
|
|
« Last Edit: September 14, 2014, 04:11:55 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
Mrz00m
Fractal Lover
 
Posts: 204
|
 |
« Reply #29 on: September 11, 2014, 03:54:41 PM » |
|
I thought the same thing as you about PI, surely they are a fractal!!! I had the same genious moment, it's true! Wow, how can a line be infinately non linear, it's a fractal linearity ?  1/ A circle can't have an infinite circumference. Dont all fractals do? It only has infinite non linearity. If non linearity can frame a fractal, then a mobeus, sinus, strange attractors, can also be considered as fractals. 2/ No fractal programs can use a circle to make a fractal, you have mix many iterations to make a fractal from them. 3/ They use Square Root to find PI. In fact they add the square root of an infinite number of numbers. Sqrts are often irrational numbers so adding an infinite number of them is super irrational. Pythagoras was obsessed with triangles and sqrt, so he sqrted a circle, that's probably all he thought about for 20 years until he decided to make the diagram that you posted. 4/ The irrational number of PI is a random theoretical number resulting from artificial "2D" construct of theoretical maths copying a random natural patterns as if they have some infinite perfection to them, which in nature can't exist, in the known universe, PI doesnt exist. The number itself is as infinitely chaotic as a circle is infinitely non-linear. In theory, perhaps the most likely pattern that you could find in PI is that it could show echoes of central symmetry, that one element of PI is a mirror image of another. Does the number that results from adding an infinate amount of sqrts together, is it more a wet biscuit than a fractal? |
|
|
|
« Last Edit: September 11, 2014, 04:02:14 PM by Mrz00m »
|
 Logged
Logged
|
|
|
|
|


















