|
jehovajah
|
 |
« Reply #195 on: April 20, 2014, 01:10:11 AM » |
|
Commentary.
Ok so I have given the background to logarithms some thought, and the claim that they are a link between arithmetic and geometric series. For me they represent a functional relationship. The notation covers over a very great deal of subjective processing and picks out only certain aspects of the total information.
Napier reputedly performed 10 million calculations, this was so his colleagues would not have to do so.
In fact Napier used the binomial expansion to structure his work, and lessen the calculation burden. The second diagonal of Pascals triangle tells him which sines to pick for each logarithm. Gradually as the index increases more of the diagonals may need to be consulted to see if they affect the 7 th significant figure, but 10^14 is a very large number, and implies the 14th significant figure would have to be factored by a coefficient greater than 10^6 in the binomial expansion.
In addition, the proportions are not equated. They are calculated and associated with a count of the number of terms factored together. Thus Napier and we have complete freedom to associate the proportions or geometrical terms to any regular dynamic or arithmetic progression. Usually these progressions represent arithmetical forms, hence the name Arithmoi in his title.
Napier associated a geometrical series of values from the sine table to an infinite straight line. However he could also, less clearly associated them to infinite sectors in a circle. Thus as each proportion is calculated it is associated to a fixed arc length. In this way the proportions turn the wheel. The value of the proportions is not necessarily connected to the rate of turn. In fact Napier specifies constant speed.
When Briggs came he was able to demonstrate that any geometrical series can be constructed by Napiers method. In fact, as this was before Descartes, DeFermat and Wallis, he could not show the now familiar log curve in Cartesian coordinate geometrical form using the logarithms as the x axis, and the proportionals as the y axis values.
The base, as we came to call it can be arbitrary, but it must have a product defined in terms of itself. In the case of the initial value for Napier it was sin pi/2 But then 1 small length had to be subtracted. If a small length element was added to sin pi/2 it would cease to be sine. It could be consecant or secant,or tangent. Instead it was given a new name as e the exponential base derived from the binomial series , over time.
We can apply logarithmic analyss and synthesis to any product algebra . Grassmann applied it to his quotient product. As far as I can tell he did it according to the rules of Napier. The fact that the products are not proportionals is of no import. If a product is defined then a logarithm function can be designed.
|
|
|
|
« Last Edit: December 02, 2014, 12:03:10 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #196 on: April 20, 2014, 09:57:53 PM » |
|
Commentary
While I cannot quite frame it yet I have the notion of the logarithm of rotations. By this I mean that rotations may be described as exponents of the exponential function, and in fact must therefore be complex or quaternionic logarithms. Whether these can be extended to n-dimensional Tensors or reference frames I do not know.
The structure of Grassmanns algebras allows for sums and products of these exponential forms as well as quotients. While Grassmann was at a loss until he researched Hamiltons Qaternions( only then realising he had solved his "looseness" problem for swivelling arms in 3d without realising) he later set a task for himself to do the incumbent processing to continue his planned development. However he died before he could make much more headway
The tantalising snippet from his proposed "Schwenkunglehre" whets the appetite and the imagination for more detail. The logarithm of rotations is precisely his idea of the log of a quotient. There he considers it to be the point of intersection of 2 lines forming the angle of swing. My notion is more related to Napier's logarithms using the sines.
By the way, it seems clear that this name is misleading. These proportions are found in the sine tables, but they are true geometric terms, the angle is insignificant to the calculation in fact the geometric mean between sin90 and sin30 is sin 45 not sin60.
The logarithms do not index angles uniformly, nor indeed the tangent line. The concordance however is fairly accurate up to tan45, by then over 4 million calculations of the proportion had been done. To get to tan60 so as to calculate sin30 2 million more calculations needed to be done.
It is not necessary to perform the calculations with these constraints as Brigg showed, but in doing so Napier reveals how logarithms can be shaped to any scale or form, as they are only indices not measures. Setting them out in a measured way allows a calculation process to trace out a form by the logarithms.
As an example, placing the logarithms uniformly on a circle drives a rotation around the circle by an infinite iteration,
Napier also placed the proportions on a line parallel to the logarithm line. He could have placed them on the radius of a circle, starting at the centre. As the sine decreased so the angle of the radius decreases and the point on the radius traces out a small semi ctcle, if it is rotated by the sine itself. But if it is rotated by the evenly spaced logarithms of the calculations it will trace out an inward spiral.
The relationship between the trig ratios is extremely convoluted. It requires the subjective process to account for orientation, direction and direction of rotation. It has multiple concordances between ratios and many surprising and convoluted algorithmic identities. Accordingly it is a rich field for meditative exploration, and a school for concepts of rotation, reflection , translation, rotational and reflective symmetries and computation.
It is the computation or arithmetic which is the odd one out! The introduction of quantity into a magnitude is simply so we can make a song and dance about it, literally. The experience of magnitude is entirely subjectiv; to communicate to an external other we have to specify and bound a region, this quantifies it and we can then communicate that specific region to an other. Depending on the conscious process of that other, they may understand the quantity on face value or as a label for the experience of magnitude .
The quantification of a magnitude always introduces a difficulty. The form or magnitude in a form is as is. The quantity we introduce is totally subjective and arbitrary. Thus as we compare,count , distinguish thus generating a logos or language model of the activity of comparison, the dynamics of it, we have no way of predicting if the comparison will be artios or perisos , perfect fit or approximate fit ( even or odd, which I hope you can see is now inane!) . Consequently we have subjectively moved from an indeterminate whole without anxiety to an indeterminate multiple form with anxiety! Will the quantity specified fit?
These specific quantities are called Metria a single ( Monas) one (en) is called a Metron. The idea of singling "one" out ( ekateros) is fundamental to book 7 of the Stoikeia of Euclid. This Monas becomes the standard monad or unit for a process of covering (sugkeime) which is done by placing the monad down(kata) onto the form/ magnitude to be measured/ quantified/ compared, and counting( Katametresee). This count is literally a cultural song and dance, by which we interact with and order space.
The form so covered by contiguous( edge joined) Metrons as monads are experienced as multiple forms( pollaplasios). But in fact they are also experienced as epipedoi or floor coverings. We came to call these things mosaics . Archeologists finding these patterns on the floors in Mousaion, houses for the Muses coined this term.
The mathematical significance of Mosaics is a fundamental and continuing analysis of the Pythsgorean school of philosophy. Indeed no Pythagorean astrologer could qualify as an Astrologer( Mathematikos) without a deep muse inspired intuition of these forms.
These mosaics did not consist of standard Metrons, ie a cube tile or a hexagonal tile, but of a mixture of tile or block forms that continuously tiled or blocked the space being compared. Thus the spaces were Topologically described and counted. Area as a standard concept of counting only standard monads is a much later idea and of a different school of thought.
Mosaics were aesthetically designed to inspire, and thus often depicted scenes as well as just abstracted patterns. Such patterns were often traces of shadow dynamics throughout the yearly cycles.
By introducing standardised Metrons, a standardised approach to topology was introduced before we came to realise how limiting that was. Also anxiety was increased because one form as a Metron does not fit all!. The proclivity for perfect fitting forms drives aspects of mathematics today, but it is perisos or approximate fits that these mathematicians see as monsters! These standardised multiple forms are called Arithmoi. Thus all Arithmoi are mosaics but not all mosaics are Arithmoi. The counting of these standard forms eventually became confusingly modified into the notion of number.
Engineers and architects however love these perisoi! These approximate fits are pragmatically engineered to construct or sculpt real objects and structures. Pragmatics chooses the best approximation for the task, and filling and smoothing gives the final fom. It is artisans and engineers who apply forms iteratively in construction projects which are grand mosaics! We live and have our conscious bring in these grand mosaical structures of our own hands and minds. And we continue to process the experiences around and in us in this way.
As much as this is formal and subjective it is also our experience that magnitude is regionalised. The very deepest meaning of this we encapsulate in the perfected magnitude, a formal creation, called the sphere.
There are 2 other formal creations which result from the deep processing subjectively of the sphere itself, These are the plane and the later straight line. Nether exist as magnitudes in our experience. We formally construct these notions from regions, that is from plane segments or line segments. In fact it is clear that the sphere is a formal construction from an iterative process of construction requiring infinitesimal regions.
The complexity of the notion has fascinated ever since it was first conceived and continues to this day. The sphere encapsulates all our notions of analysis and synthesis, all our methods or processes of calculus both differential,integral and logarithmic. All our conceptions of topology and finally all our concept of spatial mosaics.
Because we quantify and thus introduce perisos anxiety it is not surprising, after so long a time of philosophising about it that we should find some counts of seemingly unit magnitudes should involve an endless process. In fact Zeno and Parmenides drew pointed attention to this. The pragmatist had no problem identifying the solution, as do engineers. You embrace approximation!
At some stage you simply decide enough is enough! This is essentially the principle of Exhaustion! Motivating such a principle is not only tiredness but also a notion of cyclical count. This count, as a record of planetary positions became known as Time and is dynamically measured, by dynamically cyclical objects in motion. Such measures are called Metronomes!
As you can see the Metron concept underpins all our measurement, including dynamic ones.
Dynamic measures answer the Zeno Parmenides conundrum. An infinite subjective process of analysis occurs like everything else within a dynamic cycle. Thus unless we actually extend the analytical process into infinite cycles, we can stop at any cycle by design or exhaustion! In particular. We can note that Dynmical systems traverse these infinite process measurements in cyclically finite ways! That is to say I can count a number of cycles and while thus distracted a dynamic object would have traversed a magnitude I was unable to determine by an infinite process!
The issue therefore is pragmatic. Is the infinite process necessary ? The answer is no, but to be able to be as " accurate " as desired or needed is necessary. The use of the term accuracy and exact is misleading. Simply we can choose the form as the standard and then it is exactly and accurately 1 !
The underlying process is a comparison. The count is to determine a ratio. The ratio is to be reapplied pragmatically and iteratively in some construction or synthesis process. We only need to be using ratios that do not " fall over", crumble or shatter under stress and vibration! In addition, if we can we want to use ratios that are aesthetically pleasing. And we want to do most of this within the dynamic cycles of a lifetime! Pragmatics and aesthetics govern many of our most fundamental processes.
Before I finish, it is good to observe that iteration of the pragmatically generated ideal forms is fundamental to our experience of change. Having devised these forms and reapplied them to interacting with space we are reminded of why we had to devise them in the first place! Everything moves! Panta Rhei!! Our anxieties drive us to try to keep things still, but in so doing we lose contact with real life experience. We often kill the thing that caught our interest and so inspired us in the first place. However a compromise is to abstract by analogy a form and then use it iteratively to identify the dynamic experience. This is precisely how are neural networks work!
A good example is found in film or video capture. Each frame captures an analogous form to the real life object. As the cycles continue the analogous foms change and we thereby capture change by iterative analogous forms synthesised into a contiguous mosaic.of frames.
Grassmann in his analysis and synthesis intuitively understood that these forms found our notions of everything, and their mosaic combinations are the stuff of our Musings. He therefore worked very hard to establish a labelling system that made this very clear, and rediscovered a deep and abiding connection to the philosophical enquiries, observations and formulations of the Pythagoreans!
The heuristic, mnemonic and whimsical approach is actually psychologically consistent with the way we subjectively process our interactions with space.
The modern number concepts, devoid of this rich association actually obscure the natural human processes involved in the logos analogos response: how we language our experience of real life , and thus synthesise a language model of our subjective Kosmos!
|
|
|
|
« Last Edit: December 02, 2014, 02:34:41 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #197 on: April 21, 2014, 08:09:09 PM » |
|
Commentary
Lol! Norman mentions the engineer versus the pure mathematician.
While this is called the dot product Grassmann dealt with this under his quotient product.
<a href="http://www.youtube.com/v/2ZeP_Gn1x7M&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/2ZeP_Gn1x7M&rel=1&fs=1&hd=1</a>
In Norman's treatment the numbers have to be recovered or extracted from the vector. However Grassmann simply defines these line segments as what I have called trig line segments. The projection is an " arithmetic product" he says. Of course he means the product of the hypotenuse and the cosine, but in ratio form. Thus h x a/h = a where h is the hypotenuse and a the adjacent side . Thinking of the quotient a/h we see it is Grassmanns quotient operator, but restricted to the right angled triangle. Grassmann generalises this for ant line segments of any magnitude by a scaling factor.
Again the advantage of Grassmans labelling is that we can think beyond just finding a length of an adjacent side! As Norman demonstrates in this series. Lines, reflection rotation and transformations of the plane by the quotient Algebra.
|
|
|
|
« Last Edit: October 13, 2014, 07:54:31 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #198 on: April 22, 2014, 09:14:40 PM » |
|
I have rejigged some of the translations in the light of these later translations, and better resources for translating.
I think
AB + BC= AC is as important as any of Eulers fundamental equations!
It takes a mathematician and a geometer and makes them into mechanics of Nature!
|
|
|
|
« Last Edit: October 13, 2014, 07:56:01 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #199 on: April 23, 2014, 11:14:02 AM » |
|
Commentary.
The reflection of a reflection is the original; but the reflection of a reflection in a reflected mirror is a rotation of the original!
This experience highlights 2 things: reflections are reflections through a point around which point a singular rotation occurs for each point matched to each Pliny in the mirror plane. ; the rotation around one single point in the mirror plane requires an intersecting mirror precisely at that point.
By obscuring the reflection from the hidden part of a mirror plane by another mirror, we provide our subjective processing centre with additional information that allows it to factor rotation into its computations. The result is a complex Jaleidoscope image, tha subjectively regionalises all the information showing all possible results!
This superposition of solutions is regionalised because real life results occupy a region, but the multiplicity of results indicates the ability to parallel process and blend and resolve a computational result..
How do we know the result is not real? Only by comparison with other surroundings and situations, otherwise we are per force so constructed as to respond to the complex image as real!.
An insect with a compound eye has the same experience but not the ability to blend the images bifocally into a
a single depth image without visible joins. In reality we have the same bisul field experience, but we merge the boundaries after the parallel processing computes the results. The mirrors force our processing algorithm to remove the blending step in that region.
The rotation we compute in the reflected mirror is not introduced by computation. The rotation is first physically done by rotating the mirror. The computation then uses the given constraints to compute solutions.
As an academic fact geometry disregarded rotation in favour of the form. Mechanics however utilised the form to model rotation. Rotation is actually the fundamental motion in and of space, in my opinion. From it we can derive all else.
Thus when mathematicians were asked to establish a method of computing rotations, it was the engineers and Astronomers that came up with the system. Geometers were too far removed from real life to even understand the request!
Grassmann therefore arrives at an interesting time. Before Riemann asked for the help of Physicists and engineers to solve the applicability problem of academic Maths, Grassmann was having an experience that gave an answer. While Gauss was muttering over the failure of geometry and instructing Riemann to find a way round these past failures, Grassmann had sent him a copy of the Ausdehnungslehre1844 for comment. It is my suspicion that Gauss got more from perusing that draft than he realised. His busy schedule probably meant he did not give it the time it deserved, given the philosophical challenge Grassmann placed before Mathematicians. Indeed he was in danger of being called arrogant! However, gauss who did not necessarily mince his words if he felt he had preeminence was quite mild and witty in his response. He recommended that Grassmann not multiply I many new and extraordinary terms, if he wanted his work to be seriously studied! To me this indicates he read it after a fashion, but like Möbius could not make much sense of it.
However, if my experience is anything to go by , the work affects you intuitively!
Thus despite the progress on rotation in Gauss's time it is Grassmann who nails it tight in his overview. Later Hamilton acknowledges his preeminence.
Euler" s analysis of Rotation while fundamental was flawed in that he did not realise the issue of the doubling of the angle. This was caused by his arbitrary assignment of pi to the semi circle, when up to that point it was always assigned to the full circle..
The concept of rotation is still confusingly taught today, with students being given the impression that circular forces do not exist, only lineal ones do !
Both Newton and Grassmann, and many others believed in circular forces. Their labels were devised to best capture them, not to obviate them!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #200 on: April 23, 2014, 12:43:21 PM » |
|
The analysis of rotation is quite subtle, From Archimedes we get the notion of progressive orientation adjustments. From wallis a Cartrsian point version for all the Conics, and from the indian mathematicians an association with the sine and cosine ratios. Formerly it was the chord diameter ratio, and it is the chord diameter ratio that best describes rotation. While Wallis derived his equations via Pythagoras theorem, and the work of Thales and Apollonius , Newton resolved to analyse rotation in terms of the tangent and the radially directed forces, the centrifugal and the centripetal. Combining all methods he explored rotation as a projection onto the orthogonal axes of the force that acted tangentially to the circular path or course of the force, and thus always at right angles to the attractive and repulsive forces. This mechanical analysis is in fact the description of the electro magnetic combination of forces, but that was not clear to him or anyone else for that matter. Both Newton abd De Moivre used tHe ) as a constant in the unit circle to define many secret relationships between the sine / cosine and solutions to Multinomials equations of degree 2 and it's powers.mthe culmination of their work with Cotes was the Cotes De Moivre theorems of the roots of unity. Alongside these roots was the constraints I have called the zeroes of space. The logarithms of these adjugate forms sum to 0. It was votes who realised that by using the circle perimeter to record the logarithms he could write down the logarithm of the factors of 1 that is (cosx+isinx)(cosx–isinx) ix = ln(cosx + isinx) Later Euler fully derives the exponential form of Cotes discovery. This was the most celebrated formula dealing with rotation, and it made it plain rotation involves both sine and cosine. However mathematicians all over Europe were choking on the diet of negative numbers. They were positively manic over imaginary numbers! There was an intense and bloody resistance to these developments, with the preferred choice being traditional geometrical descriptions using sines and cosines. It was not untill Cayley reinterpreted the imaginary combinatorics as matrix algebras that mathematicians were able to begin studying rotation properly. Grassmann had an alternative solution to that which involved imaginary values. In fact he restated the concepts in terms of geometrical constructions. However the rotation is handled notationlly it requires orthogonal measures , arc measures and double angles! The biggest error in misunderstanding rotation comes to the so called wave mechanics. Kelvin, De Broglie and others mistakenly took the Eulerian sinf function as the model of a wave! The wave model was simplified from the vorticular dynamics of Helmholtz and Kelvin. The vortices were quietly dropped in favour of corpuscles and do the combination of cos and sine was lost. It returned later as physicists struggled to describe rotation of these corpuscles in free space. Wave or undulatory mechanics is just rotational mechanics. The forms in space are properly, vortices, and the rotations are more properly trochoids. |
|
|
|
« Last Edit: April 23, 2014, 01:00:15 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #201 on: April 23, 2014, 01:14:58 PM » |
|
There is one last fundamental aspect to rotation and that is dilation. Dilation refers to the Newtonian centripetal and centrifugal forces. We are schooled to think of rotation as circular. In general it is better to think of it as trochoidal.
When an object is rotating it experiences forces radially. Such forces are the forces of dilation. In most treatment of rotation this dilation is normalised, that is the rotation is made to conform to our ideal! In fluids the normalisation actually leads to error in the description. A rotating space dilates as a function of its environmental constraints and the energy type of the rotation. In general rotations are outwardly dilating or inwardly dilating gyres. A purely circular rotation is an equilibrium between the two dynamics.
If we can accept this as endemic within fluid rotation we can better model fluid behaviours and thus rotational mechanics. This relates then to the electro thermo magneto complexes of plasmas.
|
|
|
|
« Last Edit: April 25, 2014, 05:54:59 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #202 on: April 25, 2014, 07:53:47 AM » |
|
Commentary
I was on the bus when I finally grasped Grassmanns presentation of the quotient operator, which is an exponential operator. Crucially it elains why figure 1 in his Ausdehnungslehre is the construction of a rhombus. It is well to remember that at this stage Grassmann did not have a "solution" (Lösung) to the " looseness"(Lösung) problem of a trig line segment swinging freely in space. He only felt he had a notion for it swinging in a firmly attached (!) plane.
Having revisited the text to revise the translation of geltenden Werth and theilweise, I also realised that the complex sentence refers to " potable" values.
Gelten is an interesting concept in German. As much as I can grasp from Grassmann it is the potency or power of an idea or thing that establishes its validity or reality. Through power a thing exists or becomes..these concepts it seems are ultimately Socratic Platonic, but Hegel is the paramount modern philosopher of them!
Schliermacher is putatively said to be a major influence on Grassmann, but I think this cleric was a greater influence on Justus Grassmann and was a follower if not a student of Hegel.
In any case it is Hegel Grassmann mentions not Schliermacher.
Thus geltenden I took to mean a potable quality , in the sense that it was none zero and increasing. On further reflection I used the Newtonian idea of assignability. This comes from Newton's consideration in the method of Fluxions, where he diminishes a quantity( note , not a magnitude!) to its last assignable value. This represents, in the method of exhaustion our inability to go on with the process.
So this assignable value reminded me of the tables of values for the sine and cosines etc. within these tables are all numbers from +/-infinity to +/-1 to 0 . They nestle there in their rank and file containing a secret : the Indian decimal polynomial system!
These tables are quantitative up to exhaustion. Thus +/- infinity is written as ad infinitum, and understood not to be a number but an indefatigable process! Thus Grassmann introduces numbers in their ranks as quantitie in his geometrical constructions. The partial nesting of the trig line segments and the ordinary line segments he realised gave a metric or a quantitative evaluation to all of his geometric musings by an overlapping ratio.
In the nature of his development of his initial and fundamental " laws or rules" the preeminent symbols of which are
AB=–BA
and
AB+BC=AC
Where A,B,C can represent or label, or be handles for: points, line segments,plane segments,tetrahedral spaces, complex crystal structures etc Grassmann was granted the extra insight that 2 sorts of line segments are noted in the formal structures. The algebras for both are inter communicant, but nevertheless different. I have called them ordinary and trig line segments
He first came upon the notion of trig line segments as he reworked, reprocessed ( re-edited and redacted) the Analytical Mechanics of Lagrange. It became clear that these types of line segments, we're associated with swivelling or pivoting in the plane and in space. This swivel was first presented as a perpendicular projection, but later it was generalised by Grassmann as a type of swinging arm ( trig line segment) and producted with the exponential function as an operator. It is these trig line segments and the exponential operator that form the most general Algebra he could conceive. It is a quotient algebra,where the quotient represents the exponential operator.
The exponential operator is designated as such because it is in fact an infinite or ad finitum process..thus we cannot consider it to be a potable value in the trig tables, but it is clearly a part and mentioned in the trig tables. Thus immediatel we realise that the trig tables relate to this operator as particular and assigned values. However, the tables canbe extended at either end by this exponential process, and they canbe interpolated, again by this ad infinitum process.
In fact, within the Indian number system, the numbers themselves represent a polynomial in exponential terms, the base of which is 10.
Thus Grassmann identifies the exterior product by the swinging line segment swinging apart to get an assignable value, and the interior product by the swinging arms swinging together to get an assignable value.
Ordinary line segments have a fixed magnitude that does not therefore assume or presuppose any rotation or dynamic change in the line segment. The Algebra for that situation is clear and well defined in Grassmanns earlier work.
However for all dynamic situations the line segments need to be trig line segments. These represent fundamentally rotating space. Thus in Grassmanns Algrbra the fundamental dynamic is rotation and extension.thus the fundamental spatial orm is a vortex in the GrassmannQuotient Algebras!
The exterior product is based on fixed line segments, but they can represent dynamics by the use of scale factors. Thus these dynamics are based on transformations or extensions. For a very great many engineers and mathematicians this is sufficient to describe all kinds of dynamics even circular. But for the geometers from Newton and from Euoxus before him, the ultimate description had to be based on the sphere, and the sphere in its dynamic form is the gateway to all vortices!
When Descartes utilised the paradigm of vortices to explain orbits, it was taken seriously until Newton demonstrated a formula and a failure. The formula is now called a gravitational law; the failure was his inability to fathom the mathematics of fluid dynamics using his principles.!
Despite knowing the exponential base value, and logarithms and the binomial series and Fluxions, and infinitum processes, and the most sublime philosophy of Quantity, he could not see how to combine it all. This fell to Sir Roger Cofes as a happy and tragic moment in a worthy career! He established the logarithmic relationship
ix= ln( cosx+isinx)
Both De Moivre and Newton were on the wane in their powers of analysis, but Cotes was up and rising., when he was struck dead. The loss was palpable to Newton who remarked " Had he lived we would have learned something!"
It was about 80 years later when Euler put it all together in the Cotes Euler form
eix= cosx +isinx
and about another 60 years for Hamilton o come up with his Quaternions and the quaternionic form of this formula
eq = cosM+ LsinM
Where q= a+LM
Where a and M are " real" and L is the imaginary part of a quaternion., M being the magnitude or modulus of the quaternion.
In the meantime Grassmann had done his general analysis of how to do and learn and conceive of mathematics based on simple line segments. It was the trig line segments which in their dynamism furnished the link to the geometry and construction of imaginaries as arcs of rotation( in the plane at least). this is not to say that Hamilton did not realise this, but rather that Hamilton recognised Grassmanns formulation and expression of the idea as better and more general than his own. Not least because it avoided reams of calculations and keeping track of sign, but also because it could be generalised to arbitrary parameters( ie not just 4) .
The inner product is vitally necessary to make this quotient algebra work meaningfully.
|
|
|
|
« Last Edit: December 02, 2014, 02:46:05 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #203 on: April 25, 2014, 11:15:45 AM » |
|
Commentary. In the Grassmann " melded " notstion( zusammenhängend) which he arrived at by am intense process of reworking and editing guided by the principles of the sum and the product of line segments as constructions. Thus points A,B instruct a straight line segment. The line segment scaled constructs a ray . 2 rays construct an angle when summed, unless they are parallel, then they add or subtract quantity.( nb! not magnitude!)according to a magnitude called direction and a magnitude called orientation . The magnitude of orientation is given or presumed. The magnitude of direction is given and fixed by convention. What a line is thus becomes a moot point. Later we will find it can only really be defined by rotation about a given point! However starting with 3 points they form a line if the product BC extended= the product –BA extended indefinitely . Thus qAB + qBC =0 which Möbius used to define his line in his Barycentric calculus . Of course AB = –BA gives AB + BA =0 but this is clearly a line segment or a single ray. This formula defines direction of a ray but not orientation . The orientation is assumed given. The properties of points as generators of straight lines begs the question how? The simplest construction is by a mechanically straightened edge. But this too begs he question : how is a straight edge made? The surprising newer is by dual points constructed inside a crcle using a compass pair! Ordinary line segments are Inthe mixed or melded form cAB where c is the quantity by some measuring scheme( metric) and AB is the line segment generated with the direction A to B. In contra distinction a trig line segment exists in a relationship. At first it seems to BR by perpendicular projection Thus for for cAB and bAC we can write ccosøAC and bcosøAB. These are trig line segments in the line segments AB and AC. Now I said that it seems like these are perpendicular projections, but in fact Grasdmann introduces them as a swinging arm protected onto the horizontal position. Thus they represent a dynamically rotating ordinary line segment or an ordinary line segment that changes its orientation relative to a perpendicular to a projection line segment or if you prefer a start position for the swinging ordinary line segment. These trig line segments thus have a particular role: when considering geometry in dynamic relative rotation to its initial conditions these forms of line segments are fundamental. Now the Algebra while being inter communicant with the ordinary algebra for line segments has a remarkably different product rule due to the cosine circular function and in part the hyperbolic cosine function. This can be constructibly demonstrated using the rhombus construction in figure 1 The processing of the labels is subtle. First  is used to identify a corner angle, not to measure it. So how do we measure it? ā is used to symbolise a measurement in radians. So now we can say  = ã radians. But since  is only labelling a corner we can replace it by another label. In this case it is the product ab where a and b are trig line segments( because we are dealing with relative rotations) ab is thus a parallelogram product, in which case it is an inner product because these are trig line segments, or it is an intersection point for the 2 trig line segments. The appropriate interpretation is the intersection point. The reason being that the inner product becomes 0 at 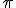 /2. The intersection point not only labels the point where the angle is located but so the trig line segments that form the angle. What it does not do is quantify or measure tha angle. That has to be done by the appropriate radian measure. Now we can establish the operator as a quotient that multiplies, pro icing the Algebra with a new type of notation to perform multiplications. This notation is a logarithm of the exponential. Thus all multiplication can be done by addition of Logs! In one fell swoop Grassmanns notation allows quotient multiplications to be done by logarithmic addition, in addition the quotients are clearly the corners of the geometric inner product. Thus we have a geometrical representation of quotient multiplication which is clearly angular addition. These angles are corners of inner product parallelograms so now rotations can now be represented by logarithms which add like angles, are measured in radians and which look like inner product parallelograms! The quotient notation or labelling can then be used to transform trig line segment quotients into exponential operators recording and manipulating rotations. As you can see, no normal to the plane is required , but the line segments do have to be trig line segments to function properly. The beauty of trig line segments is that if you fix their relative orientations they can be treated as ordinary line segments. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #204 on: April 26, 2014, 04:20:05 AM » |
|
Commentary
Eiø = coshø+ i*sinhø
This analog suggests itself or reveals itself from Grassmanns argument for a construction of the imaginary magnitudes. Using the E instead of e is to remind one that the hyperbolic functions are to be used , and thexprct hyperbole not circles
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #205 on: April 26, 2014, 01:40:52 PM » |
|
You cannot serve God and Mammon!
This ecclesiastical dictum, put into the mouth of Jesus, shaped the course of Prussian mathematics and ultimately it's groundbreaking impact on Western thought!
The debate arose as a religious difference. The philosophical differences had been simmering for centuries. Galileo and his Memesis Garibaldi, Descartes and Leibniz, to name but a few. But in Prussia , the political and national turmoil brought about by several humiliating defeats by the French led to the debate about reform. The chief philosophical argument for reform was that of Humboldt. He recognised that if Prussia was to survive it needed self actualising individuals who would think creatively for themselves, for their futures and ultimately for the future of Prussia! The evidence seemed to be demonstrable in the burgeoning uccess of the French and their imperial conquests. New ideas, new technologies and new politics were all evident in the French " revolution" .
In order not to be engulfed by these revolutionary passions Prussia had to reform, and Humboldt focused on education. In the meantime the ecclesiastical powers were fighting to maintain their control over education. Their enemy was not the emperor of Prussia, but the burgeoning industrial concerns in the rest of the world. This was Mammon!
The growing success of technologies made certain groups and individuals very wealthy. It enabled them to demand certain things of their workforce and certain protections of their intellectual and industrial properties. Rural Prussia , the power base of the clerics was increasingly made to compete with these demands and repeatedly failed to deliver the social and economic goods! God it seemed was on the side of the industrialists!
The theosophical debate was whether God actually intervened in the world, and if so how? On the one hand clerics were preaching faith in a god who shapes history especially the Holy Roman Empire now seated in Prussia, while industrialists were pointing out that those who held a mechanical philosophy were receiving more of the earths bounty. The debate was very divisive with the rtionalists( those that believed in gods revlatIon through Jesus) accusing all others of being irrational. The debaters broke into schisms and dome even came to blows and pitch battles.
In the midst of this, a new philosophical breed of clerics struggled to provide sneers. Schliermacher, Hrgel, Kant all were engaged in the debate, while Humboldts followers eventually pressed the advantage and got the imperial seal on a sketchy programme of educational reform.
It was meant to involve all the society in the debate and it had to, because there was no 5 year plan, just Humboldts ideas! Everybody was executed to bring their expertise to the tak, and all levels of society in education were expected to mingle to discuss how to bring it about. The natural meeting places were the universities as such, nd all teachers were called to meetings, iscusdions, debates on the way forward, intermingling with the academics and the philosophers.
It was at such meetings that a young Justus Grasmann first heard the call and dedicated his life to educational reform in Sczeczin. This is how the Grassmann came to be involved in the topic of the Ausdehnungslehre.
In the meantime Kant had managed to broker a peace between the warring factions about God and mammon, now represented as man's ingenuity, on the bais of ome fine philosophical argumentation, and the work of Newton. Newton was widely regarded in Prussia as an apostle of God, bringing god' s truth about the laws of nature. Thus, despite Newtons unconventional beliefs, he was used to join together believers in a truce. All would wait and see how god would unfold the universe according To Newton's laws. If so then Gid cited and it was described by mathematics!
This is for me a great fallacy, but even in Kant's brokered peace there were dissenters. Mathematics was not rational and thus revealed and handed down by god; instead it was constructible, and arrived at by the hands and minds of men!
The debate became: was Mathemtics discourive( revealed in iscusdions with god and others) or constructed?
It turned out that Justus believed his tutor that it was constructed and set out to prove it in Geometry! Really it was to establish it in arithmetic, but he could not found multiplication logically either in Algebra or arithmetic or even logic itself! His resort was to geometry or confusion!
His problem was not his analytical ability, or his rigid formalism, it was Aristotle ! Immediately it was Legendre's Euclidean Geometry, which was a concoction of parts of Euclid's Stoikeia and Legendres own pragmatic approach informed by his engineering and Mechsnical background. In addition he was schooled in the Aristotelian system developed by Aristotles Lyceum and copied by the Islamic scholars. Thus few realised the difference between Playos Academy and Aristotles Lyceum. They were deemed to both be Platonic. But in fact The Academy was Pythagorean! Aristole rejected several key Pythgorean notions particularly in regard to Arithmoi! Thus Aristotle's teachings were Platonic, but no longer faithfully Pythagorean.
The view of the Stoikeia, when it was made public was that it was a Greek geometrical text after the fashion of Aristotle? Nothing could have Ben Rutherford from its purpose!
The philosophical introduction which the Stoikeia constitutes is markedly different from he Aritotelism introduction to rhetoric, grammar and logic! In addition, the Stoikeia is Muse lead, requiring the student to meditate and seek guidance by the muses. Aritotle replaced the muses by Peripatetics! These were teachers who walked up and town in front of a class! This was unheard of before! Students gathered round a seated teacher hoping to eavesdrop on his conversation with his chosen students!
Thus the philosophy of the Stoikeia does not sit well with the Aristotelian pedagogic or logical approach!. Grassmanns attempts to " fix" geometry was misguided by Legendre, and many others before him. The case of the 5th postulate is the most famous embarrassment of the era. It culminated in so called nonEuclidean Geometry which turned out to be a version of ancient and well used and researched spherical geometry!
Gauss was appalled and embarrassed and hot Riemann to throw out a challenge to engineers and physicists! Essentially it was a request for help to get Maths back on track, dealing with real world probems based on a real well founded Grometry or set of geometrical notions..
The solution fell to Hermann Grassmann. It turned out that though it was innovative and entirely novel thinking on his part, he had managed to recapture Pythagorean thinking and thought process.. His approach involved tackling the philosophical Kantian issues first , using to him a clearer version of Hegelian dialectic.min so doing he created a work, part time, and in between very demanding periods of his life , which fundamentally shook the philosophy of Peano, A N Whitehead, Hamilton, and a number of others internationally. However it did not seem to have affected Gauss!
We see that to this day Mammon won the argument. Mathematics had to deliver technological benefits! They were called for by Riemann and thus Gauss. They were worked on by the Grassmanns, and Now they underpin all our modern mathematically nd theoretical physics.
This is why Hermann was at pains to point out all his proofs were constructible!
|
|
|
|
« Last Edit: April 27, 2014, 10:05:39 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #206 on: April 28, 2014, 01:22:00 AM » |
|
Commentary. I have reviewed the translation of the section on the imaginary magnitudes, in the light of Grasssmann knowing and studying the work of Euler on the circular functions. In this regard the whole passage represents hiscanlysis nd reworking of Euler's wok in tems of the sum and product of line segments, however it is crucial that the line segments are trig line segments. In this section he discusses the cos line segment snd the sine line segment.. Given these 2 line segments he is able to use an snakogy with the sinh nd the Cish circular functions, by imagining the sin as the sinh and the cs as the cosh. He then derives Eulers formulae from the line segment sums , taking care to rotate the swinging are by 90° to get the sine analogy correct. However his argument or presentation relies on the identity e ix= cosx + isinx which is derived from the infinite series expansions by Euler. That being given one can demonstrate theat Coshix = cosx And sinhix = isinx Thus e  is relateable directly by the imaginary arcs to e i(a)The fact of the matter is that neither sinh or cosh are close to sin and cos in tabled values, so such an equation is not sustained for "real" values. However for these imaginary arc values they mysteriously work! What Grassmann is showing is that geometrically these processes make sense. In particular they make sense as rotation. One new analogue in Grassmanns promoted idea is that i not only rotates the plane , and every line segment in it, it also necessarily rotates every circular arc segment concentric to the centre of rotation. . Rotating arc segments takes us into the concept of phases and phase angle! A phase essentially is a notion of a position or status in a cycle . Thus i changes the phase of a rotation by pi/2. The arc logarithms is another new concept. An arc in a sector marked out by two radii can be defined as the logarithm of the quotient of these 2 lines. We could say that degrees are the logarithms of the 1° sector, with the 2 radii forming the intersecting lines of the quotient operator. While we tended to just measure Grassman realised that a product could be formed that rotated the swinging arm or arc round the disc. The addition of angles was now able to be viewed as logarithms of a proportioning process, ie a geometric mean process. The exact nature of this process is discussed usually under the heading of the roots of unity. These come about as a result of the Cotes DeMoivre theorems. In this sense a degree is the 36o th root of unity , while i is the 4 th root of unity. As Grassmann observed the Menge or crowd of all these different logarithmic scales or logarithmic schemes is infinite in magnitude! Because we are so poorly educated we do not currently know these things! When I was developing the polynomials of rotations thread I had only intuition, and brute force to guide me. I made many mistakes, based on false assumptions and did not realise how to get from one firmly fixed plane of rotation to another. It is heartening to realise tha neither did Grassmann at this stage, and Hamilton had sent some 10 years blundering into his solution! The importance of parallel or concentric motions came to me later. Eventually I was able to construct the Newtonian triples, something Hamilon was not able to achieve satisfactorily. This all by flashes of insight into this analysis here! |
|
|
|
« Last Edit: April 28, 2014, 02:15:16 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #207 on: April 28, 2014, 02:03:12 PM » |
|
Commentary
It seems plausible that Grassmann in the section on the development of the inner product into the quotient algebra, introduces a a third type of line segment: the hyperbolic trig functions line segment!
Not only does this extend the generality of the trig line segments it suggests a future development of the line segment types into the general function line segment.
Such a ,one segment would essentially be n ordinary line segment with a function as a factor in a product with the quantity of a line segment. In one development I can imagine using functions bases on the trig tables, in another line of development I can think of new tables being developed by using the richt angled triangle to measur off points along a general curve..
I did this for Theodorus spiral and developed a function called sint= øsinø. Plotted against cos it gives a spiral .
The possibilities are endless.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #208 on: April 28, 2014, 03:23:50 PM » |
|
Commentary
While not earth shattering it is important to realise that the line segment AB fir example is a representation of a family of parallel line segments throughout space.
Thus when Grassmanns quotient operator swings a line segment into another orientation it swings all the family into that orientation. This is the meaning of his statement about every line segment in the planar case. However, this makes a point not unique in space, but rather a representative of a family of points!
To specify a unique poit we have to actually uniquely identify it. Even if I uniquely identify it that is only with regard to a uniquely identified reference frame! Thus every aspect of our mathematics is relative and subjective. The only invariants are formulaes expressing invariant relationships As everywhere in space. This is a big assumption, and one that needs to be empirically justified.a formal proof is just an illusion in this case?
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #209 on: April 30, 2014, 11:30:40 AM » |
|
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










