I would not want anyone to go away with the notion that the complex numbers are inherently complex as they are not.
Firstly they are not numbers but trigonometric ratios written in a polynomial form.
Secondly they are not complex but they are applied to geometrical situations that look simple but turn out to be complex!
In fact what we have in the past termed complex is better described by thr notion "fractal" as commonly used in these times.
I know some would like a strict definition of fractal, but the genie is out of the bag and normal language development of meaning now applies.That more often than not is a good thing as it indicates spreading of the idea to the general consciousness, and providing confusion is headed off at the pass can make communication simpler.
Most of us are familiar with negative numbers but maybe not understanding that their proper name is directed numbers, as they have a geometrical application beyond double entry book keeping. As a consequence we may be familiar with the rotation of the number line to describe negative values. We however are misdirected precisely at this point in our understanding.
We may then come across the trigonometric ratios and the importance of direction and quadrant without ever making the connection. We may then be introduced to the weird and wonderful world of complex arithmetic through the imaginary "route", exploring briefly and confusingly the roots of x^2+1=0. Again no understanding or explanation that makes sense is usually given, and the relation to trigonometry is totally void.
Finally vectors may be thrust upon you with the trigonometric conversions and no understanding of where you are, where you have just been, and where this is all leading you toward!
I hope that fairly explains an initial interaction with the so called complex numbers.
In my experience one never quite gets over the √-1!
So lets get over it together.
First of all directed numbers are a special case as they only address opposite directions! What if a directed number is not in an opposite direction, how do we notate that?If you keep this question in mind then everything else becomes real simple.
We chose, confusingly i think, + and - for the opposite directions, but what did we choose for other directions?
Bombelli attempted to set up a notation for the other directions but was cunfused himself. He chose +√- (piu di meno) and -√- (meno di meno).
This was quite a complex sign which for a long while had no commonly accepted geometrical meaning, but which for Bombelli and Descartes always meant at right angles to!
Therefore as geometers they always looked and moved at right angles to the +- direction in their geometry.
When it became popular to use their system by fixing the ordinate and coordinate in the page then the right angles direction became known as y. Thus historically y came before i but they both represent the same thing, the orthogonal direction to the +- direction you define on the page.
To say this became obscured is to make an understatement.
Most of us have heard the rule of thumb:
the square root of a number is that number you have to square to get the number you start withSome are familiar with its origin in the geometric mean a*b=x^2 for a pair of crossed lines divided in the ratios a:b and x:x.
These in turn are magnitudes of similar triangles where a:x=x:b for corresponding sides. Thus the geometrical construction of finding the geometrical mean underlies the expression "to square root"
When directed magnitudes are introduced into the geometry what we find is that square rooting involves a rotation through π/2 from the positive direction, in either an anticlockwise or clockwise rotation.
Thus, very straightforwardly and without any artifice the square root of a magnitude in the negative direction involves rotating clockwise or anticlockwise by π/2We simply have to set up some convention for these rotations and the simplicity is made secure.
So for example √-1 may be defined as a clockwise rotation by π/2 and -√-1 as an anticlockwise rotation or vice versa. However The Bombelli operator does the job perfectly and should be retained as the standard.
So the rule of thumb then becomes: the square root of a directed magnitude is the rotation of the direction by π/2 and the geometrical mean of the magnitude, under the rules of operation described by Bombelli.We need only now to realise that √-1 is a trigonometric ratio called
)
if anticlockwise rotation is defined or
)
if clockwise.
The definition of √-1 is implicit in the trig identity:
geometric mean of
)
=
)
*
)
From which we derive
)
as a directed magnituce with direction radial
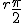
in the unit circle and magnitude unity from the unit circle.
It is to be called the fourth root of unity, thereby recasting all numeral schemes as scalars of roots of unity. Our understanding of measure is to be derived from this basis, making -1 simply a measurement in the direction - of 1 unit magnitude, and allowing such measurements in an infinity of directions denoted by radial directions in the unit sphere, with a special subset in the unit circle.
In the unit sphere we define the eighth root of unity for the sphere as
In 3 dimensional spherical
) geometric mean of(geometric mean of(
geometric mean of(geometric mean of()
,0,0
) *(
)
,0,

)
)Where the magnitudes of the vectors/ tensors are used.
From this we see that a matrix or tensor format is desirable over a linear form, but a linear form can be written with the additional conventions that the axis are represented by orthogonal vectors, and the aggregation is an algorithm for defining a position in 3 space.


















