|
jehovajah
|
 |
« on: October 13, 2008, 01:12:05 AM » |
|
The operator is i
|
|
|
|
« Last Edit: February 01, 2011, 03:42:23 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
cKleinhuis
|
 |
« Reply #1 on: October 13, 2008, 09:12:31 AM » |
|
very good statement   the operator i stands for a number whiches square root is -1  a complex number is made upon a number 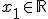 and a number 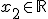 times the virtual number 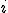 , those two numbers are written ) this is a complex number http://en.wikipedia.org/wiki/Complex_number |
|
|
|
« Last Edit: October 14, 2008, 11:36:13 AM by Trifox, Reason: added latex code »
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
|
|
jehovajah
|
 |
« Reply #3 on: November 19, 2008, 11:55:26 PM » |
|
The statement itself arose out of being pressed for time but i wanted to intimate the distinction between the concept of number and the concept of operator. Number is a quasi mystical concept with a long philosophical tradition. At each historical advance along the way to our number system the operators have been minimised in favour of the concept number. However the very methods that were being codified or explained were introducing a complex or systematic set of operations on either the numerals or the variables or the shapes and now even on the regions of space. The operations are what are overlooked. Nowadays we call these complexes of operations algorithms. Your algorithm for constructing a complex number is not rigorous enough and only delineates the form. The uperator +i rotates the numeral it is next to through 90 degrees to the number line. This spatial movement is represented in the x,i plane. This is mathematically no different to the x,y plane. So the so called complex number is formally equivalent to a number pair or more rigorously a numeral pair. The properies of the operator i are therfore crucial for determining the actions on the numeral pairs. All these operations/ properties can be represented in the matrix notation making even clearer the operative nature of i.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #4 on: October 25, 2009, 04:52:54 AM » |
|
 i was taught arose out of being unable to solve for the roots 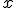 2 2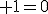 . However it seems that they arose in an algebraic context while the solution for the roots of quadratic, cubic and quartic polynomials as we call them were being sought. They were a pure invention whose use was not fully appreciated until euler, and later. Euler recognised their rotational value but not that they are an operator. In field and ring theory today they are still treat as a number. Euler's identity  ipi ipi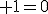 allows a number value to be arrived at in certain instances but his formula clearly shows that i is an infinitely termed operator equivalent to the two angle operators sin and cos in an algorithm. The operator i acts on the numeral pairs ) transforming them to ) a rotation of the plane through  . Using the Euler formula we can specify the angle of rotation more precisely. Thanks to euler the role of the operator i can be specified and it is not part of the numeral system. 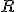 x 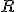 is a better description of the field of application of i and the field in which any fundamental theorem of polynomials needs to be established. To extend this operator to 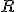 x 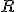 x 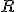 we could define it as operating on the plane (x,y) followed by on the plane (y,z). This can be extended to higher surfaces. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
Cyclops
|
 |
« Reply #5 on: November 30, 2009, 02:19:10 AM » |
|
very good statement   the operator i stands for a number whiches square root is -1  a complex number is made upon a number <Quoted Image Removed>and a number <Quoted Image Removed> times the virtual number<Quoted Image Removed> , those two numbers are written<Quoted Image Removed> this is a complex number http://en.wikipedia.org/wiki/Complex_numberFox,what do those symbols € and R represent in your statement?(I cant replicate what you typed on my phone) |
|
|
|
|
 Logged
Logged
|
Sensitively dependant on initial conditions  |
|
|
|
cKleinhuis
|
 |
« Reply #6 on: November 30, 2009, 02:25:46 AM » |
|
Fox,what do those symbols € and R represent in your statement?(I cant replicate what you typed on my phone)
this is standard math notation, "R" stands for the Real Numbers ( 3.14.. ) , there also exists "I" for integers, or Q for rational numbers ( 1/2, 1/3...n/m ) so, and the € (  ) stands for is element of in the stament above i just wanted to say that x1 and x2 can be real numbers ... |
|
|
|
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
David Makin
|
 |
« Reply #7 on: November 30, 2009, 02:27:54 AM » |
|
very good statement   the operator i stands for a number whiches square root is -1  a complex number is made upon a number <Quoted Image Removed>and a number <Quoted Image Removed> times the virtual number<Quoted Image Removed> , those two numbers are written<Quoted Image Removed> this is a complex number http://en.wikipedia.org/wiki/Complex_numberFox,what do those symbols € and R represent in your statement?(I cant replicate what you typed on my phone) "a complex number is made upon a number x_1 \in \mathbb{R} and a number x_2 \in \mathbb{R} times the virtual number i , those two numbers are written (x_1+x_2i) this is a complex number" x_1 € R == x_1 is a member of the set of real numbers x_2 € R == x_2 is a member of the set of real numbers At least that's what it means using the correct symbols - I couldn't work out how to get them either  |
|
|
|
« Last Edit: November 30, 2009, 02:30:22 AM by David Makin »
|
 Logged
Logged
|
|
|
|
|
cKleinhuis
|
 |
« Reply #8 on: November 30, 2009, 02:41:36 AM » |
|
the laTex notation for those is: x_1 \in \mathbb{R} = 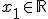 x_1 \in \mathbb{Q} = 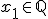 x_1 \in \mathbb{N} = 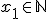 use the latex button to insert the <tex> tags in your posting the "_" sign stands for sub writing, the "\in" standsfor "is Element of, or is In Set" the "\mathbb{}" statement does some magic to encode the symbol you want to display in double dashed characters "HELLOWORLD = \mathbb{R}"= 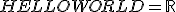 <- define a set "x_{downunder} \in \mathbb{HELLOWORLD}" = 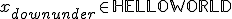 this is how the above lines look in sourcecode of a posting "HELLOWORLD = \mathbb{R}"=[tex]HELLOWORLD = \mathbb{R} [/tex] <- define a set
"x_{downunder} \in \mathbb{HELLOWORLD}" = [tex] x_{downunder} \in \mathbb{HELLOWORLD} [/tex]
|
|
|
|
« Last Edit: November 30, 2009, 02:54:36 AM by Trifox »
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
kram1032
|
 |
« Reply #9 on: November 30, 2009, 04:16:35 PM » |
|
=-1 |^2<br /><br />x = (-1)^2<br /><br />x = 1<br /><br />sqrt(1) = -1<br />) as lyc said:    * sqrt(-1) = sqrt((-1)*(-1)) = sqrt(1) = 1<br />) be careful, that notation leads to a problem, proofing wrong all the previous maths. So you can't say =i) because that would lead to the caluclation above. Instead, i is defined as the number/value to give -1 when squared 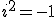 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Cyclops
|
 |
« Reply #10 on: November 30, 2009, 05:05:08 PM » |
|
<Quoted Image Removed> x = (-1)^2 x = 1 sqrt(1) = -1 " border="0" align="absmiddle" /> as lyc said:   <Quoted Image Removed>-1 = i*i = sqrt(-1) * sqrt(-1) = sqrt((-1)*(-1)) = sqrt(1) = 1 " border="0" align="absmiddle" /> be careful, that notation leads to a problem, proofing wrong all the previous maths. So you can't say <Quoted Image Removed> because that would lead to the caluclation above. Instead, i is defined as the number/value to give -1 when squared <Quoted Image Removed> <Quoted Image Removed> x = (-1)^2 x = 1 sqrt(1) = -1 " border="0" align="absmiddle" /> as lyc said:   <Quoted Image Removed>-1 = i*i = sqrt(-1) * sqrt(-1) = sqrt((-1)*(-1)) = sqrt(1) = 1 " border="0" align="absmiddle" /> be careful, that notation leads to a problem, proofing wrong all the previous maths. So you can't say <Quoted Image Removed> because that would lead to the caluclation above. Instead, i is defined as the number/value to give -1 when squared <Quoted Image Removed> I'm afraid this is all gobbledeegook to me! I'm fascinated by numbers but am uselsess at math and never did algebra at school-you might as well be typing in Swahili! :S |
|
|
|
|
 Logged
Logged
|
Sensitively dependant on initial conditions  |
|
|
|
jehovajah
|
 |
« Reply #11 on: December 05, 2009, 03:23:08 AM » |
|
The problem here is not you cyclops but the notion that maths is these symbols. I bet this would look great in swahili and probably more inviting! You are fascinated by number you say. so were the Pythagoreans, the Indians, the numerologists etc. Modern math has tended to downplay this great driving force engaging individuals in the playfulness of math. However, math is just thinking about the experience you have of what is going on around and inside you paying particular attention to iterative features of that experience. It is the iteration that drives the interest in quantification, boundarisation, geometrication, pattern and syntax. In a straightforward way iteration makes "numbers" so fascinating. It is in exploring this that i have come to realise that certain things are not numbers no matter how many times they are called numbers. Here i found a link to a discussion about the operator i and its development http://i-is-no-longer-imaginary.gmxhome.de/ . I have seen the dramatic push this operator has given to the development of modern math, but how mathematicians still have not tidied things up. The complex string a +b*i is no more a number than p and q are numbers. When Al Jabr was published by Muhammad ibn Mūsā al-Khwārizmī it was specified after the indian practice of letting any mark colour or symbol stand for a numerical value But the literal strings formed with operators were always aigorithms. Algorithms are extended operations, and this indian conception was and is a study of the fascinating subject of operators.I have identified the enfolding set of operators as being a set which i call 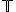 the set of transforms. Alongside this set is the fundamental process for which and from which these transforms were created : Iteration. The greatest achievement of this operator i is to have brought iteration to the fore. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #12 on: January 19, 2011, 10:38:51 AM » |
|
It seems obvious now, but i think it is worth pointing out:
The magnitude denoted by i is a constant. It is a fundamental constant of not only our universe but probably all universes we can apprehend.
I have learned a lot since i started this thread, and i would not agree with myself now. I is a constant magnitude, but not a number and also not an operator! i am hoping to classify it as an orientation, with some help.
|
|
|
|
« Last Edit: April 09, 2012, 03:40:24 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
ker2x
Fractal Molossus
 
Posts: 795

|
 |
« Reply #13 on: January 19, 2011, 10:58:04 AM » |
|
not a number and also not an operator! Ha ! i'm not confused anymore. thx  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #14 on: January 31, 2011, 12:40:22 PM » |
|
I think i can establish now that √-1 was effectively the y axis orientation, before Descarte's coordinate and ordinate system. That When he mentioned this coordinate system in his mathesis, Descartes used the opposite side of a right angled triangle as his coordinate and the adjacent side as an ordinate, and thus subsumed Bombelli's distinction within a scheme of his own. Then by calling √-1 imaginary he dissuaded any close examination of the similarity between him and Bombelli for hundreds of years,
The trigonometric relations were not affected, but because of the confusion, scientists did not know how to connect the y axis and the right angled orientation to this disparaged negative magnitude!
If it were not for Wallis Napier,Newton, Cotes And De Moivre, i think science would have been harmed by this although mathematics so called may have explored imaginary numbers as an oddity in Number theory.
"i" then is no more or less than the unit of the scaled orientation we call y, it is an oriented magnitude, a directed number of magnitude one and direction π/2 and related to the trig of the unit sphere indissolubly .In so far as 1 is commonly called a number it is able to accept that denotation, However, strictly it is a unity, or a unit magnitude after the greek, and a yoked magnitude after Brahmagupta.
A full explanation has been arrived at in the Bombelli operator thread.
Sorry if i have caused any confusion over the years, but it has been quite an investigation and i hope it has cleared things up for any one interested. It certainly has for me.
|
|
|
|
« Last Edit: January 31, 2011, 12:57:03 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|


















