|
jehovajah
|
 |
« Reply #15 on: February 01, 2011, 03:17:03 PM » |
|
Finally i can ask the sensible question: what is the square root of a magnitude that is directed in the direction π!
On the face of it there should be no difference to the square root of a magnitude whichever direction it is measured in, but there is and the reason is because the magnitude is rotating!
So the question is : what is the square root of a magnitude that is rotating between 0 and π? we have to take the orientation of the resultant into consideration, because all our magnitudes are in free rotation.
Thus the answer is :half the rotation and the square root of the magnitude!
You can generalise it to any root.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #16 on: February 02, 2011, 06:50:49 AM » |
|
I have found the most wonderful site for any researcher! Here i have found Riemanns collected works in german! And of course understandings of the foundation of mathematics untrammeled by ignorance. Good luck in your studies! |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #17 on: February 10, 2011, 09:55:06 AM » |
|
Watched a programme on Fermats last theorem, the modern proof. Well Fermat would certainly not have proved it that way! I suspect Fermat's proof would not satisfy todays rigorous standards. Fermat knew about Diophantine numbers, and i suspect he conjectured his proof based on the relation ^n+(sin\theta)^n \neq R^n) the radius of a circle |
|
|
|
« Last Edit: March 08, 2013, 08:37:29 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #18 on: July 20, 2011, 05:25:43 PM » |
|
Complex vector algebra is how i refer to this topic now. i.j,k are orthogonally oriented vectors. The properties of a complex vector space reflect all the properties of so called complex numbers through the product rules of complex vectors. The myth of number is what has caused the difficulty in accepting directed vectors, and the √-1 is a red herring. People hate negative numbers and that hatred passes on to anything to do with them. But everybody thinks they know what number is and yet they cannot explain what it is easily, so how are they going to do with negative numbers or roots of negative numbers.
Numbers have a place but not at the foundation of mathematics. Euclid placed "numbers"about 2/3rd of the way through his elements, because they actually derive from geometry.
Trig ratios are fundamental, and vectors are representations of trig ratios.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #19 on: September 03, 2011, 09:35:37 PM » |
|
i have done a lot of work on generalising the notion of sign without realising that i was in fact generalising it to unit vectors!
Thus i can entirely replace sign by the notion of a unit vector. However to reference the orientation of a unit vector i used the convention of radials emanating from a spherical centre with the radian measure specifying the direction from a pole and a perpendicular rod along the great circles.
Thus spherical geometry had the answer along with everything else.
Now here is the trick, by prefixing or postfixing a radial to a magnitude we create a vector.
The radial clearly records rotational orientation , thus the notion of a vector is linked to rotation, clock arithmetics and moduli. The notion of reflection in a centre of rotation is therefore to be distinguished from the notion of radial orientation .
We do not need to worry about addition subtraction and general aggregation structures, the familiar rules apply, but with consistent significance. We do not get the notion of the √-1 we instead get the notion of the √L1 if L is the left pointing unit vector.
We only get i if we understand that √ is notation for the geometric mean, and in that case we expect not only√1 but also the U vector giving U√1.
We then need to define U•U=r•R•r•R =L that is some aggregation operation produces L from r•R aggregated against r•R. "r" is some action on vectors. (confused? i know i am! And that is the point. The definitions of i are in confusion!! instead of using the notion of "multiplication" we in fact just rotate. The action r is in fact "rotate to vector radial + π/2", and we do not use i as a number but as an instruction)
These unit vectors when employed as gnomons for aggregation have to produce a consistent result. The gnomon may be a curved gnomon and it acts on a vector.
When looked at in this way the complex decisions and aggregation structures that are being chosen are revealed, but they are all understandable and not mysterious or imaginary.
This also seems to be done in isolation but in fact it is done in analogy with a fractal scale of other relations. This is the genius of Hamilton's exposition of complex algebra.
Thus i replace sign by a vector and the sign rules by a set of operators or actions that give the required results . Unit Vectors with a set of actions replace the complex number notion.
|
|
|
|
« Last Edit: April 09, 2012, 04:33:37 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #20 on: January 01, 2012, 11:19:04 AM » |
|
I have recently posted some links to material that makes intelligible the actual proceses involved in apprehending√-1, and places Hamilton and Grassmann in Context. http://jehovajah.wordpress.com/jehovajah/blog/the-ideas-that-led-to-quaternionsAlthough the material contains mathematical notation, the sense is well explained without needing to understand the notation. By this you may come to realise the struggle that took place to find an intelligible notation for the field of "sets" , and how expediency has led to your mathematical education being a melange of half baked ideas. In any case enjoy and deepen your knowledge of where fractals "come" from in space. |
|
|
|
« Last Edit: October 15, 2014, 03:26:12 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #21 on: May 13, 2012, 10:15:24 AM » |
|
|
|
|
|
« Last Edit: October 15, 2014, 03:28:31 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
hgjf2
|
 |
« Reply #22 on: May 13, 2012, 05:03:34 PM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #23 on: June 02, 2012, 03:14:11 AM » |
|
...
 You know me too well! |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #24 on: March 08, 2013, 11:53:11 AM » |
|
I was in conversation with a research scientist just the other day and he was bemoaning ) And I thought " Haven't I dealt with this subject in one of my posts?" Well I have revisited it here thinking hmm I have forgotten so much! The confusion created by this particular piece of conventional notation is profound. It turns the world of mathematics upside down and sets it into a flat spin! I refuse to engage with this notation nowadays. Instead I view it as a procedural call in a computational language. The procedure or algorithm it specifically calls depends on the argument of the call ie the context. Now, when I say I refuse to engage with this notation I do not mean I do not note and value it's significance. It is an invitation to engage in what Hamilton called the mathesis of the imaginaries. This mathesis is hidden away in algebra, as a subject boundary and particularly in abstract algebras. If we take Algebra to be a blind persons geometry then the symbol becomes a braille mark alerting the reader to this singular fact. The plane is not the real world! One cannot model a 3d world in a 2d plane! We have to go off piste!( pun also intended). In reality 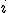 is a label as is 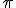 and they both alert to the rotational dynamic in Spaciometry. The procedural call is to some process algebra of rotation. ) is also a functional symbol that has to hang about in process algebras awaiting it's sequential call. In these cases it highlights a meta algebra, a meta mathematics which more prosaically I identify with any sufficiently high level computer programming language that has a mathematical and statistical sub routine library. This is fair, and in fact invigorating. It means that we can dispense with mathematics as a singular discipline and place the content securely within the contexts of computational science and philosophy. The only recognised person, after Newton to attempt such a transformation is Hermann Grassmann in his Ausdehnungslehre of 1844. The version his brother Robert masterminded in 1862 is far removed from Hermanns original conception. That he was able to draw attention to the similarities and developments of his original ideas is perhaps what illustrates the applicability of his original notions. You see, by my meanderings, where this topic leads and always must lead away from mathematics so called to a broader process algebra, even beyond group and ring theoretical analyses. That we can watch a 3d animation is a consequence of the actual meaning of ) ! |
|
|
|
« Last Edit: July 14, 2013, 10:03:32 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #25 on: May 23, 2013, 09:55:17 AM » |
|
The nature of i is discussed in this thread http://www.fractalforums.com/new-theories-and-research/geometric-algebra-geometric-calculus/msg61550/#msg61550in which the symbolic complexity is demonstrated, as it represents the geometrical form and trans-form-ation. I think i have already made the statement that i and √-1 shhould now be clearly distinguished. One is algebraic and a constant proportion, the other is a complex label that acts as a mnemonic during actual arithmetical calculations. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #26 on: July 11, 2013, 02:24:02 PM » |
|
I always advise completely ignoring 'i' except when (in)formally demonstrating the product. Once that's done, you never need it again. It's nothing more than a comma or period past that point...or a typographic element to denote which of the two linearly independent 'parts' one's talking about. i = sqrt(-1) is at best very misleading and at worst completely wrong (depending on how you interpret the expression).
|
|
|
|
« Last Edit: October 15, 2014, 03:31:30 AM by jehovajah »
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #27 on: July 16, 2013, 01:41:04 AM » |
|
Euclids Stoikeioon book 5 helps to explain where the confusion derives from.. The Greeks and the Indians had no concept of negative magnitudes. There was also no concept of multiplication. They also had two concepts of duality. http://jehovajah.wordpress.com/jehovajah/blog/2013/07/14/isos-and-analogos-different-notions-of-dualityBecause of these precursory facts, one has to understand Brahmagupta and Bombelli exactly as they wrote and thought. Quantity was factorised into multiples, and they were aggregated or disintegrated. Brahmagupta did not introduce negative magnitudes, rather he demonstrated how Shunya was at the back of everything. If we subtract what we have we can easily see Shunya. And what we have to subtract is multiple if what we have is multiple. In explaining this he utilised analogous duality, straight from the Eudoxian concept of analogos and logos.
<a href="http://www.youtube.com/v/UcZ9HhVck9Y&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/UcZ9HhVck9Y&rel=1&fs=1&hd=1</a>The question of the rule that a rectangle formed from a pair of magnitudes that are going to be subtracted should be aggregated does not make sense in an isos duality. The issue never arises practically. It is only in an analogos duality that this rule makes sense. This is because of the single rule that magnitudes must be of the same kind to be compared, aggregated or factorised. Logos analogos constraints , applied rigorously mean that algebraic rules are the foundation of Arithmetic. The creation of natural numerals, and then fractional numerals and finally negative numerals were on the basis of the logos analogos duality. The isos duality was restricted to direct geometrical comparisons. In this case negative quantities are geometrically rotations of magnitudes. On the page they look no different to any other geometrical construction. However analogos duality requires 4 magnitudes, and a negative magnitude is drawn within a gnomonic form, where the parts to be subtracted actually have relative positions! This formal presentation of a magnitude with a subtracted magnitude, forces the requirement of an additional magnitude. This rule is expressed as – * – = + in Bombelli's notational rhetoric. But Brahmagupta had explained this in his treatment of analogos duality. These rules actually arise in the cubic setting, and it is only in that case where 3 pairs of magnitudes are compared and each magnitude has a part subtracted, that the full rule appears. However, to reduce it to a rule of signs requires the creation of negative magnitudes, as opposed to parts to be subtracted in the process. In isos duality the ) is no different to the 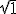 . All quadrature is done in the circle, using chords crossing the diameter perpendicularly. Only by using rotation orientation as a distinguisher can any distinction be made , but it does not actually uniquely define a value. On the other hand analogous duality does enable a unique representation in notation.. The rise of coordinates and complex combinations as vectors has meant that the imaginary quantities can be distinguished in coordinate notation. The myth created around so called imaginary numbers can be dispensed with and more accessible rules and notation can be used. We do not, as a rule seek to confuse our colleagues if we make a mathematical discovery in these days. However, in the past it was a recognised way of determining primacy to send out or publish a confusing or coded message. |
|
|
|
« Last Edit: October 15, 2014, 03:46:52 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #28 on: October 23, 2013, 12:44:04 PM » |
|
Believing that I was some mathematical entity, Clifford went on to use it in the further development of his algebras. http://rsta.royalsocietypublishing.org/content/356/1740/1123.full.pdfIn this regard, I has become a behavioural marker, guaranteeing a predictable mathematical behaviour. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #29 on: April 30, 2014, 01:28:30 AM » |
|
<a href="http://www.youtube.com/v/oybzcvv-ZVo&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/oybzcvv-ZVo&rel=1&fs=1&hd=1</a>
I have placed this here to avoid jamming any ones computer! It is very relevant to the work of Grassman as it occurs historically after he has written and published the Ausdehnungslehre 1844. However it shows little trace of Grassmanns concepts, and consequently it is quite hard to follow . After Riemann's death Mathematicians turned to Grassmanns work to make sense of Riemanns !
The work of Gauss similarly in 1827 the year Justus published a paper on Trigonometry in space, contains some concepts of Euler regarding parameter switching and surface analysis by tangent planes. The linear combination of the map from the parameter plane to the surface, and then from the surface to the unit sphere for the normal to the surface shows ideas that are similar to Hermans but not expressed in terms of vectors, or dot products etc. Thus Hermanns concepts are in keeping with his times, but add that extra insight that makes the difference for the general mathematician.
Gauss may have had a good grasp of what he meant but without the presentation of Hermann Grassmann it was very difficult to follow his argument or disquisition
<a href="http://www.youtube.com/v/drOldszOT7I&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/drOldszOT7I&rel=1&fs=1&hd=1</a>
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|


















