|
jehovajah
|
 |
« on: January 08, 2009, 11:28:48 AM » |
|
By recognising i as an operator on the set of reals we can come to see how we can use the fractal formulae for the various julia sets to describe or rather iterate to real objects. Most work being done now is using i on the 2d plane called the complex plane but this is a misnomer. i on the 4d tensor is being studied the so called quaternion. Only a few mentions of i on the 3d tensor have i found. Any references would be appreciated.  |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
lycium
|
 |
« Reply #1 on: January 10, 2009, 07:31:15 AM » |
|
Most work being done now is using i on the 2d plane called the complex plane but this is a misnomer. i on the 4d tensor is being studied the so called quaternion. why is the complex plane a misnomer? also, i'm fairly sure you meant 4d vector? |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #2 on: April 21, 2009, 12:15:16 PM » |
|
Hiya, not been around for a few months so sorry taken so long to reply.
Tensor maths has vectors as its operational domain. So yes you can use vector interchangeably here. Tensor math is however more general than vector math. The complex plane like cantors infinities are part of the folklore of math. Rigorous definitions of these entitiies exist which are algebraic rather than geometrical. i operating on the reals is called colloquially the complex plane. The structure is an isomorphic map of the operation on the reals to the domain of the 2d tensor, or 2-tuple tensor or 2d vector. How we referrence this to make it of use artistically or engineeringly is part of the experimental nature of math, and in any case is wholly iterative or recursive over any sequence. Several other new operators have been proposed nullity and infinity seeming to be the newest. But in reallity any algorithm is an operator on the domain for which it was created.
|
|
|
|
« Last Edit: October 11, 2011, 09:27:43 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #3 on: October 20, 2009, 09:33:25 AM » |
|
Here is a guy who uses a modulo 9 math group with the numerals 1 2 3 4 5 6 7 8 9 with an additional operator he calls the name of god petroglyph. Now the interesting thing here mathematically is how the operator is defined and then applied within the math operation rules to geometrical space in particular on the surface of a torus. It clearly shows that operators or algorithms in general have to be defined and studied to extract there applications and significance in or to geometrical space. It also shows the power of mystical numerology in the inventing of mathematical method and research. It is for this reason why math is so hard for the average jo and jane, because of it mystical origin and manipulation. However that does not make its insights to the originator wrong , simply difficult to communicate or transfer.
Enjoy this presentation and learn a lot.
<a href="http://www.youtube.com/v/fbFhi7eKwJU&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/fbFhi7eKwJU&rel=1&fs=1&hd=1</a>
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #4 on: December 05, 2009, 03:40:55 AM » |
|
A tensor as opposed to a vector allows for a more generalised treatment for reference systems at any point. Suffice it to say that by exploring a surface as a tensor allows many things to be determined about that surface using other representational systems. In a way this leads to self similarity with other representational systems and an insight into other equivalent ways of describing the system/surface. This may allow or arrive at a solution that cannot be so easily seen in another representational system.
I have seen my request for action on the 3d tensor more than adequately answered in the recent search for the 3d mandlebrot.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
Paolo Bonzini
Guest
|
 |
« Reply #5 on: December 10, 2009, 09:39:53 AM » |
|
I have seen my request for action on the 3d tensor more than adequately answered in the recent search for the 3d mandlebrot.
Note that an algebra on the 3D tensor as you call it was sought for decades. In the end mathematicians appreciated that there is no such thing, and that when you want to operate in 3D you have to use either quaternions, or vectors and matrices. In either case you end up doing the same calculations, just with different notations (quaternions with a real component represent an orthogonal matrix multiplied by a scalar, and 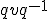 replaces matrix multiplication 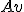 ). |
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #6 on: December 10, 2009, 08:30:57 PM » |
|
afaik, it had to do with the rotational degrees of freedom. I can't be sure of course but I guess, triplex algebra, while finally being a 3D algebra, can't really be used for rotation stuff... Actually I wonder what a rotation represents in that case, as on one hand, 2D-algebra is enough to do 2D rotations but 4D algebra is needed for 3D rotations.... Either, 3D algebra is like eulerian rotations which have the gimbal-lock problems or they would correspond to some weird 2.5D rotations or something like that... (Would actually be interesting to derive fractals from their dimensional properties, rather than searching for the dimension of existing fractals... - if one could do this, there might as well be ways to extend that to normally illegitime notations like a fractal with dimension 4, living entirely in dimension 3, if that in any way ever could actually make sense  ) |
|
|
|
|
 Logged
Logged
|
|
|
|
|
LesPaul
Guest
|
 |
« Reply #7 on: December 12, 2009, 11:07:36 AM » |
|
Here is a guy who uses a modulo 9 math group with the numerals 1 2 3 4 5 6 7 8 9 with an additional operator he calls the name of god petroglyph. Now the interesting thing here mathematically is how the operator is defined and then applied within the math operation rules to geometrical space in particular on the surface of a torus. It clearly shows that operators or algorithms in general have to be defined and studied to extract there applications and significance in or to geometrical space. It also shows the power of mystical numerology in the inventing of mathematical method and research. It is for this reason why math is so hard for the average jo and jane, because of it mystical origin and manipulation. However that does not make its insights to the originator wrong , simply difficult to communicate or transfer.
Enjoy this presentation and learn a lot.
<a href="http://www.youtube.com/v/fbFhi7eKwJU&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/fbFhi7eKwJU&rel=1&fs=1&hd=1</a>
This is only loosely on-topic for this forum, but did anyone else watch this video? It's a 44-part (yikes!) lecture where he talks about his "discovery." As far as I can tell, his discovery is just what any freshman math major would call "modulo 9." He writes out the numbers 1-9 around a ring and proceeds to fill hours and hours talking about the symmetries that result, but I really didn't see anything more complicated than "modulo 9." He seems fascinated with the fact that if you add the digits of a base-10 number (over and over until it becomes a single digit), that's the same as taking that original number modulo 9. I don't think this is unique to base 10... I'm just guessing, but I would think that in any base N, taking a number modulo (N-1) would do the same thing. He also points out that if you start with 1 and repeatedly double (2, 4, 8, 16, 32), you get a repeating sequence in his modulo-9 world: 1, 2, 4, 8, 7, 5, 1, 2, ... And he's also fascinated with the fact that you never hit the numbers 3, 6, or 9, but I don't think that's any mystery -- it probably just has something to do with relative primes? There really isn't any more math than that, but he somehow makes the leap to suggesting that our base-10 system is the secret to the inner workings of the universe. But you could choose just about any base you like and find just as many (or more) symmetries, circular patterns, etc... Sorry to ramble about it, but I just donated several hours of my life to that guy's endless discussion of basically nothing, and thought maybe I missed something... ? He claims to have "solved" pi and reduced it to a rational (I think), and also to have "solved" the primes, and then he goes completely overboard and says that he has mastered space travel, zero-point energy, black holes, you name it... but somehow doesn't ever cover any of that in the actual lecture. |
|
|
|
« Last Edit: December 12, 2009, 11:10:30 AM by LesPaul, Reason: Corrected math »
|
 Logged
Logged
|
|
|
|
|
cbuchner1
|
 |
« Reply #8 on: December 12, 2009, 02:52:53 PM » |
|
Enjoy this presentation and learn a lot.
As far as I can tell, his discovery is just what any freshman math major would call "modulo 9." Too funny. But still, even very simple maths problems often have highly intriguing and fascinating outcome and can be studied ad infinitum. z^2 + c, anyone? It's just that in this video the guy probably didn't know about any "prior art"  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #9 on: December 19, 2009, 09:46:46 AM » |
|
The point of modulo 9 arithmetic is not the simplicity but the application. Math includes mystical and practical thinking in its historical development. Modern math has "wondered" off into an arid desert of abstraction and lost the engaging playfulness that is core to the exploration of mathematical thinking. I am sorry that you did not get much math out of viewing , but the fact that you viewed a large section of these videos is testament to their engaging nature. We tend to be steered into thinking math is this one thing and it has to be hard and we have to not understand it! My point will always be that math is a playful thought adventure which has a value to the players and may just provide a useful way of encoding or describing aspects of others experience. It has always been used like this and always will. The trick is to get paid while you are playing!
So now when Hamilton thought he could extend his theory of couples to triples and finally settled for quaternions did anyone pay attention to his motivation or explanatory schema? It was to establish a mathematics of time! He was trying to amongst other things explore a philosophical notion of time current in his day. in doing so he explored the most complete algebra of the so called complex numbers you will find, and all engagingly written and accessible if you are not put off by a bit of notation.
@paolo, I am sure that you have a point if you maintain the traditional schema, but for a moment explore the idea of unary operators and designing algebras around their properties. I have not written a reply to kujonai and ted yet, but i see their identity rule as only one possible manipulation of the mod(n) unary operators. Who knows if this won't provide further insight into the so called triplex algebra that is non quaternionic. For example mapping the mod(3) unary operators to the complex plane is only one useful mapping.
|
|
|
|
« Last Edit: October 11, 2011, 09:32:45 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #10 on: December 19, 2009, 10:12:42 AM » |
|
I have seen my request for action on the 3d tensor more than adequately answered in the recent search for the 3d mandlebrot.
Note that an algebra on the 3D tensor as you call it was sought for decades. In the end mathematicians appreciated that there is no such thing, and that when you want to operate in 3D you have to use either quaternions, or vectors and matrices. In either case you end up doing the same calculations, just with different notations (quaternions with a real component represent an orthogonal matrix multiplied by a scalar, and 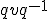 replaces matrix multiplication 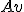 ). One interesting study Paolo is the development of matrices and vectors, not just there manipulation. These procedural forms and there syntax can do so much more than what we are usually taught. I have long thought that 3d is a misnomer, as one requires at least a 7 component tensor to describe a coordinate system, these being the initial extension, the 3 angle rotations to describe orthoganality and then the three extensions along the orthogonal axes so formed. Of course orthoganality though desirable is not necessary. This then begs the question : what is dimension? Tensors seem to me to provide a more genartal algebraic foundation to component forms or ntuples. |
|
|
|
« Last Edit: October 11, 2011, 09:34:34 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #11 on: October 11, 2011, 09:46:05 AM » |
|
It seems a long time since i looked at this topic, but in fact i have never let go of it. My blog has details of my latest adventures in Wonderland! Anyone for tea?   it turns out Hermann Grassmann has been exploring the 3 tuple as a combination of punkt and the bivector. But it also turns out that the so called 2d system is actually a 3 tuple system with one of the vector components ignored or subsumed. Whi would have guessed? |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|


















