|
jehovajah
|
 |
« on: January 27, 2010, 04:45:35 PM » |
|
So just to start off with a+ib is polynomial of degree 1 in i.
This makes perfect sense NOW, especially as i realised that they arose as the solution to polynomials that otherwise had no real solution. HISTORICALLY mathematicians had been used to giving solutions in surd form so a+b√-1 had the right form but no real decimal name in the namespace. However i now see that these are polynomial solutions to polynomial equations. I will call them polynomial numerals. Later I will term them polynomial unary operators or polynomial rotations.
|
|
|
|
« Last Edit: January 28, 2010, 08:37:37 AM by jehovajah, Reason: correction »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #1 on: January 27, 2010, 05:07:11 PM » |
|
I have to acknowledge the influence of kujonai and timgolden in formulating the basis of unary operators by exploring the notion of sign. My interest in the operators of the set FS under iteration have led me to reconfigure foundational notions of math. Unary operators came from understanding the action of i and j. This was then extended by understanding sign, a unary operator mod(2). Some of the language will have to be decided, for example polynomials of degree or power or signal 2!
|
|
|
|
« Last Edit: January 27, 2010, 11:41:57 PM by jehovajah, Reason: finish »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #2 on: January 28, 2010, 08:36:19 AM » |
|
Kujonai also introduced the mod(n) categorisation which means that the logarithmic additions are mod(n) clock arithmetic. This means that the actions of the unary operators on themselves are added mod(n) and thus we can think of them as acting in a kind of multiplicative way. So a unary operator acting on another unary operator is a product mod(n).
For example sign acts on the real numeral 2: sign02 =+2 and sign12=-2
sign1sign02=sign1+02=sign12=-2
sign1sign12=sign1+12=sign02=+2.
The indices to sign i have called signals. They look and act like powers mod(2). In polynomials they may also get referred to as degree. These notational references speak of the history of notation more than anything else, but it is important to be clear from the outset that these indices refer to the action of an operator on an appropriate operator not to numeral manipulation,numeral products or numeral multiplication. Therefore i retain the term signal. This means that if sign is taken as the nomial polynomials in sign will all reduce to signal 1 polynomials mod(2)
sign02+sign12+ sign22+sign32
=2sign02+2sign12
signal 0 is defined as the identity signal and as we have seen the identity signal on sign means that a positive sign is symbolically attached.
Now i can use a consistent geometrical representation of a unary operator as long as i clearly define what that is. For this discussion i am going to define unary operators as acting in a plane only. I am implying that i can define them as acting in geometrical space but it is a bit of a tort to do so without establishing the definition in the plane first.
To have any geometry we need a specific orientation first. This orientation is essentially not definable by any geometrical reference frame i construct with it. So to be literal it is ground 0. Because of this every reference frame is relative to the observer, and it is only by agreement we construct a common reference frame .This orientation is the axiomatic orientation. However it helps me to see that a general property of space is orientation. i have a special capacity to fixate on a specific orientation and reference from that orientation.
Another fundamental property of geometrical space is extension . Orientation and extension are logically and practically inseperable and a sensory synaesthesia. The third fundamental of geometrical space for our discussion is rotation, and again this is inseperable from orientation and extension. However, customarily we ignore the sensory synaesthesia because we are not reference free, we live in a gravitational geometrical space and that determines our orientation fundamentally and frictional forces determine our rotation.
Nevertheless we need three fundamentals to establish a geometrical space : orientation, rotation, and extension. Of the three orientation is the ground 0 and cannot be defined,and extension can then be defined as being in a certain orientation (direction) and rotation defined as around a certain orientation (axis). I am going to use the notion of axis and axes to refer to an orientation different to and from the axiomatic orientation, and to give axes therefore there own extension and rotation. Because of this an axis will have a direction in the plane referenced from the axiomatic orientation.
I will define as a scale a division iteration such as: divide into 10 parts a unit length. This iterated will produce the real numeral scale along the axes. From the axiomatic orientation i define unary operator cycle mod(1) to be a rotation about any axis that returns to the axiomatic orientation . I define the unit length as sweeping out a circle radius 1 circumference 2π and the axis of rotation as being always right to its direction which in a mod(4) unary operator scheme will be identified as π/2, and the axes under cycle mod(1) i define as sweeping out a plane, which makes a normal to a plane (the axis of rotation under cycle mod(1)) the definition of that plane. AS the mod(n) n increases i can define a scale by division iteration: divide 2π into n parts. However we normally use: divide the unit (radius) into 10 parts divide the cicumference into parts that are equal to or fractions of the unit (radius). By this more complex iteration we construct a radian measure of rotation.
It is worth noting that geometrical space has all these attributes but we only distinguish them under some operation,and the vector notion ought really to include rotation as axiomatic and within its definition, thus a vector has magnitude direction and rotation.
|
|
|
|
« Last Edit: February 16, 2010, 06:17:12 AM by jehovajah, Reason: clarification »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #3 on: January 28, 2010, 09:45:38 AM » |
|
I am going to use 3 mod (4) unary operators to construct a reference frame for geometrical space. As you will see this means i am going to construct polynomials of signal 3. Signal 0 will be as defined above the identity or axiomatic orientation for that rotation, ground 0.
The unary operators are i,j,v. They operate on the numeral line.
i only operates on i,j on j, v on v.
The operators act on the real numeral line which is the basis of the axes and to which rotation is imparted orthogonal to the direction of the axis, that is to say that an orthogonal axis to the axis in focus rotatates around that axis. However this implies and is made explicit that there is always an axis orthogonal to both that defines the plane the first two axes in focus are in. So i have our 3 requirements for the vectors orientation and an axiomatic orientation which is to the right of the screen for the positive numeral line (by the way sign is preserved in an even mod unary operator scheme), extension along the numerate axes, and rotation defined by i,j,v.
The reference frame is constructed. Thus the following rules describe the constructed scheme.
i,j,v are unary operators in a specified plane.
Using the real numeral line as the axiomatic orientation i can define i as rotating in a plane that goes into the page away from this orientation, j as rotating in the plane of the page away from this orientation and v as being aligned so that its axiomatic orientation goes into the page and it rotates in a plane coming out of the page orthogonal to the i and j planes. This makes all the normals to the 3 planes orthogonal to each other, and if i take 0 as the "origin" i have the familiar octant division of geometrical space.
i0=1 i0 which is the direction of the real number line.
j0=1 j0 which is the direction of the real number line by construction.
v0= 1 v0 which is the direction into the screen achieved by rotating i00 by i1.
i0=1i0 the identity rotation with extension 1, i1=ii0 a π/2 rotation of the orientation, i2=i2i0 a π rotation of the orientation, i3=i3i0 a 3π/2 rotation of the orientation, i4=i0 a 2π rotation of the orientation.
j0=1j0 the identity rotation with extension 1, j1=j j0a π/2 rotation of the orientation, j2=j2j0 a π rotation of the orientation, j3=j3j0 a 3π/2 rotation of the orientation, j4=j0 a 2π rotation of the orientation. The plane of this rotation is orthogonal to the plane of the i rotation.
v0=v0 the identity rotation of v with extension 1i=1ii0, v1rotates v0 to j10=v10 a π/2 rotation of the orientation, v2=v2v0 =i30 - v20 a π rotation of the orientation of v, v3=v3v0 =j30= v30 a 3π/2 rotation of the orientation of v, v4=v4v0=i10=v0 a 2π rotation of the orientation. The plane of this rotation is orthogonal to the planes of the i and j rotations.
These rotations are quantized, which is a result of the definition as mod(4) unary operators. I point out that all complex math is so quantized and the amount of quanta is some power of 4.
|
|
|
|
« Last Edit: May 22, 2010, 07:45:59 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #4 on: January 29, 2010, 09:51:40 AM » |
|
So referring back to my vector definition , the axes form a set of orthogonal vectors each being the norm to a plane and each importantly having rotation included by definition. I will write the tensor (i0,A1,A2,A3)
where A2,A3 refer to the orthogonal axes with extension and rotation inherent, and i0 refers to the orientation.
I can now rewrite this tensor as (i0,(ei0,v),(ev0,j),(ej0,i))
where ei ej ev are extensions in the directions i0,j0,v0 and i,j,v are the unary operators providing quantized rotation.
Because of the extension on each axis i can use scalar multiplication on each axis, but this operates as a unary operator only on the extension not the rotation.
Focussing on the rotations i can write the position of a point as a polynomial of rotation from the orientation thus
(x,y,z)= xi0+yi1+zj1
Where x is the extension along the axiomatic orientation,y the extension along the axis formed by the rotation i1 and z the extension along the axis formed by the rotation j1.
To clarify matters i define i0,j0,v0 as being of unit extension, these then become scalar products as desired.
An important note is that by design i0 and j0 are interchangeable as are i20 and j20 and v0 and i10 and v10 and j10, v20 and i30 and v30 and j3 0.They are only references to the same orientation (as are i0 0 and j00) so you cannot rotate v0 in the planes for i and j! thus i*i≠v0*v0
Another interesting point to me is that setting the scalar to 0 does not remove the rotation. it simply gathers that rotation to the origin where it remains as an infinite potential, still quantized and still seperate from any other rotation that has been gathered there by setting the scalar to zero!
While i can now refer to any point in the octants by a rotational polynomial, i have not accounted for all the rotations by using the common form of notation.
writing (x,y,z)= xi0+yv0+zj1
is better but means that rotations are independent or dependent , for example i cannot do v0 from the axiomatic orientation without doing an i rotation first. I will cover this in the next post.
{September 2013, i learned that rotations act on the cylinders around an axis! so this restriction i laid on the topic was why it was so hard to grasp what was going on!}
|
|
|
|
« Last Edit: September 12, 2013, 11:45:54 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #5 on: January 31, 2010, 04:35:15 AM » |
|
| xi0 | yi | zj | xi2 | yi3 | zj3 | | | | | | | | yv0 | zv | | yv2 | zv3 | | | | | | | xi0 | x2i0 | xyi | xzi0j | x2i2 | xyi3 | xzi0j3 | | | | | | | | xyi0v0 | xzi0v | | xyi0v2 | xzi0v3 | | | | | | | yi | yxi | y2i2 | yzij | yxi3 | y2i0 | yzij3 | | | | | | | | xyiv0 | yziv | | y2iv2 | yziv3 | | | | | | | zj | zxj | zyji | z2j2 | zxj3 | zyji3 | z2j0 | | | | | | | | yzjv0 | z2jv | | yzjv2 | z2jv3 | | | | | | | xi2 | x2i2 | xyi3 | xzij | x2i0 | xyi | xzi2j3 | | | | | | | | xyi2v0 | zxi2v | | xyi2v2 | zxi2v3 | | | | | | | yi3 | yxi3 | y2i0 | yzi3j | yxi | y2i2 | yzi3j3 | | | | | | | | y2i3v0 | yzi3v | | y2i3v2 | yzi3v3 | | | | | | | zj3 | zxj3 | zyj3i | z2j0 | zxj | zyj3i3 | z2j2 | | | | | | | | yzj3v0 | z2j3v | | yzj3v2 | z2j3v3 | | | | | | | yv0 | xyv0i0 | y2v0i | yzv0j | yxv0i2 | y2v0i3 | yzv0j3 | | | | | | | | y2v0 | zyv | | y2v2 | zyv3 | | | | | | | zv | zxvi0 | zyvi | z2vj | zxvi2 | zyvi3 | z2vj3 | | | | | | | | zyv | z2v2 | | zyv3 | z2v0 | | | | | | | yv2 | yxv2i0 | y2v2i | yzv2j | xyv2i2 | y2v2i3 | yzv2j3 | | | | | | | | y2v2 | zyv3 | | y2v0 | zyv | | | | | | | zv3 | xzv3i0 | zyv3i | z2v3j | zx2v3i2 | zyv3i3 | z2v3j3 | | | | | | | | zyv3 | z2v0 | | zyv | z2v2 | | | | | |
Table of actions on quantized unary operators mod(4) i 0 is the orientation from which all other rotations are measured anticlockwise. By construction j 0 is interchangeable with i 0 and j 20 is interchangeable with i 20. The unary operators i,j,v are rotations by π/2 in a plane, each plane constructed as orthogonal to the other two. v 0 is thus the orientation for v rotations and is not interchangeable with a j or an i rotation. However v 0 is referenced by an i rotation and not by a j rotation. Geometrically the system can be represented by rotations of a vector which has magnitude, orientation and rotation inherent, and graphically we can represent this by a scaled line with spin orthogonal to its extension. This scaled line we define as an axis and the i,j,v as rotatations of a unit extension on the axes. The rotation v 0 is dependent on i and j in this system, but only as ways of referencing the outcome of each of 4 unary rotations under v. Thus the rotations are independent but rule bound as shown in the table above. i cannot act on j. So ij =ji is defined by the orientation acted on. i 20 and j 20 being interchangeable allows ij 2 to become ii 2 which can be resolved as i 3 but only when acting on an i rotation. Where i and j are symbolically written as acting on each other the action is defined only by the orientation acted on . This system allows me to write a polynomial that represents a cartesian triplex or a complete polynomial that represents 8 cartesian points at once. (x,y,z)= xi 0+yi+zj. This represents a point in the first octant obtained by rotating the extensions from i 0/j 0. The extensions are x,y,z and are scalars 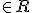 . Writing them in the ordered triplex form can now be seen as a matrix of coefficients. The nomial matrix (i 0,i,j) has i highest signal of 1 I allow other nomial matrices of unary rotations such as (i 0,v 0,j) or (j 0,v 0,j 3) etc. (x,y,z,x,y,z)= xi 0+yi+zj+xi 2+yi 3+zj 3 is the highest signal polynomial i can write and is the basis for the table above. As i see it the axes cover all the octants and so this polynomial represents the 8 points of an object centred on the origin. Thus (1,1,1,1,1,1) are the coefficients for a cube length 2 {September 2013. I was very confused in this post and in fact misleading about the actions. The axes and the rotation operators are confused in this post. I correct this later on but it was a struggle!} |
|
|
|
« Last Edit: September 12, 2013, 11:53:24 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #6 on: February 02, 2010, 06:13:27 AM » |
|
(x,y,z) 2=(xi 0+yi+zj) 2= | xi0 | yi | zj | | xi0 | x2i0 | xyi | xzi0j | | yi | yxi | y2i2 | yzij | | zj | zxj | zyji | z2j2 |
But (x,y,z) 2=(xi 0+yv 0+zj) 2= | xi0 | yv0 | zj | | xi0 | x2i0 | xyi0v0 | xzi0j | | yv0 | yxv0i0 | y2v0 | yzv0j | | zj | zxj | zyjv0 | z2j2 |
Both tables express the squaring of the polynomial rotations for (x,y,z) but the first is with reference to the axiomatic orientation i 0 , the second is with respect to 2 orientations i 0 , v 0 . To plot this i need to show what happens to the orientations under the new rotations and from that what happens to the coefficients . This then gives me the position the pont is moved to. Now sign is the other unary operator which acts in the plane as a π rotation. Thus sign 0v 0=v 0,sign 1v 0 =-v 0=v 2 a π rotation from v 0so sign 0i 0=i 0,sign 1i 0 =-i 0=i 2 a π rotation from i 0sign 0j 0=j 0,sign 1j 0 =-j 0=j 2 a π rotation from j 0. Similarly sign 0v 1=v 1,sign 1v 1 =-v 1=v 3 a π rotation from v 1so sign 0i =i ,sign 1i 1 =-i =i 3 a π rotation from i 1sign 0j =j ,sign 1j =-j =j 3 a π rotation from j 1. |
|
|
|
« Last Edit: May 19, 2010, 07:58:57 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #7 on: February 04, 2010, 04:31:30 AM » |
|
So the rules, just to be rigotous are: | i0 | j0 | v0 | : | i | j | v | : | i2 | j2 | v2 | : | i3 | j3 | v3 | | i0 | i0 | j0 | v0 | : | i | j | v | : | i2 | j2 | v2 | : | i3 | j3 | v3 | | j0 | i0 | j0 | v0 | : | i | j | v | : | i2 | j2 | v2 | : | i3 | j3 | v3 | | v0 | i0 | j0 | v0 | : | i | j | v | : | i2 | j2 | v2 | : | i3 | j3 | v3 | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | | i | i | i | i2 | : | i2 | X | X | : | i3 | i3 | i0 | : | i0 | X | X | | j | j | j | X | : | X | j2 | j2 | : | j3 | j3 | X | : | X | j0 | j0 | | v | X | X | v | : | v | v2 | v2 | : | X | X | v3 | : | v3 | v0 | v0 | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | | i2 | i2 | i2 | v2 | : | i3 | X | X | : | i0 | i0 | v0 | : | i | X | X | | j2 | j2 | j2 | X | : | X | j3 | j3 | : | j0 | j0 | X | : | X | j | j | | v2 | X | X | v2 | : | v2 | v3 | v3 | : | X | X | v0 | : | v0 | v | v | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | | i3 | i3 | i3 | i0 | : | i0 | X | X | : | i | i | i2 | : | i2 | X | X | | j3 | j3 | j3 | X | : | X | j0 | j0 | : | j | j | X | : | X | j2 | j2 | | v3 | X | X | v3 | : | v3 | v0 | v0 | : | X | X | v | : | v | v2 | v2 | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
A table of the associative actions of unary operators It is clear to me that these associations are not commutative or associative in general. The X indicates actions that have no physical, geometrical or logical action. The simple rule is a rotation can only affect axes in its plane of rotation.However the orientations are non rotations so they have no action on any rotation. They serve to apply the extension to the axes being acted on in the association. A couple of interesting notions that occur to me is that sign although a rotation of π in a plane is also a reflection through the centre of rotation. So rotation has a special transform called reflection involved with an axes . This property is a special combination of the rotation and extension and orientation already defined in the vector called an axis and does not need to redefine a vector. Reflection occurs only when one axis is rotated and only when that axis is in the direction of the reflection and the π rotation is in the vertical plane of that direction or is a π rotation of the horizontal axis in that direction. A rotation in the horizontal plane in that direction is a simple rotation. A π rotation of 2 axes produces a reflection through the origin of rotation, which is the same as a rotation to that position. A π rotation of 3 axes gives a reflection again. |
|
|
|
« Last Edit: February 17, 2010, 03:22:44 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #8 on: February 06, 2010, 04:57:33 AM » |
|
{September 2013 This is where i realise that rotation operators are different to orientations! But more subtly the orientations are labels and the labels remind us how the orientations transform when operated on by the rotations . My notation makes explicit what Hamilton was thinking, but loses the fluidity of his presentation}
There is an important distinction i am making between rotation and orientation . Rotation acts on orientation and results in an orientation. Defining i00 as the initial orientation and in0 as orientations resulting from in rotations i can represent the distinction between the i and j and v rotations.
As i defined the in0 are all orientations in a plane.jn0 are in a different plane and vn0 are in another plane. i,j,v are the unary operators for those planes, so no matter what i associating with j cannot be a rotation in a plane unless j rotates jn0 onto a in0.
it is therefore necessary to know which orientations are being rotated and by how many times. Where the resultant orientation falls determines whether the association can act or whether it fails to have an effect, Thus the table of associations above are based on rotations from the orientations of the system in the planes of the system. Thus i2 is the rotation acting on i00 resulting in orientation i20.
ij are the rotations acting on j00 or i00, Whichever i choose the association fails. j rotates j00 to j10, but now i cannot rotate the resultant orientation. Similarly j rotates i00 to j10.
Now by construction j00 and i00 , j20 and i20 are orientations in the same plane so i orj can rotate them but only as an i or j rotation, thus giving an i or j orientation.
Also by consruction j10 , i10 , j30 and i30 are orientations that lie in the v rotation plane. Thus v00 is i10.
Now i3 acting on j only works if j rotates j10 or j30 onto the i plane of rotation. It does not work if j rotates i00 or i20. So it is necessary to know which orientation is being rotated.
Where the X are is where i have made the observation that the first rotation acting has rotated the orientation into a plane the second rotation cannot act on. in this scheme 2 important orientations are rotated v00 or i00. In one instance i have had to emphasise that iii=ii=i=v0 v0 v0 = v0v0 = v0. These associations of i have to be mapped to the rotation that defines v00 very carefully.
(x,y,z)= (xi00,yv00,zj10). This can be written as a polynomial rotation
(x,y,z)= (xi0i00+yii00+zji00) or
(x,y,z)= (xj0j00+yij00+zjj00)
I can then "factor out" the orientation to isolate the rotations
(x,y,z)= (xi0+yi+zj)i00
This then puts the table of actions in context and the table of associations can be used to determine a resultant orientation that is valid.
I did think about using 0 in place of X but this is not just about neutering senseless associations but about reading the signals of what rotations are happening that would be missed.
I think that a lathed mandelbrot is sculpted because the quaternion math accentuates a v rotation under iteration unless missing terms are replaced.
|
|
|
|
« Last Edit: September 12, 2013, 12:03:16 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #9 on: February 07, 2010, 11:46:33 AM » |
|
I am going to call the reference frame i am constructing an initial reference frame. Whether it is the same as an inertial reference frame is a question for later. Using this initial reference frame as a basis i can define the position of origin of any relative reference frame and its orientation using the tensor (i0,ei00,v,ev00,j,ej10,i).
It is clear the quantized rotatations i,j,v are not subtle enough to describe any orientation in geometrical space,but again a later post will consider this. If i refer to this relative frame as XYZ, then it is important to observe that the association ji and ij have a effect on XYZ: they spin XYZ around the v00 or the j00 orientations. This means that far from j acting on i having no sensible meaning it in fact refers to an action on the rotation attribute of each axis. That is to say that if it were possible to quantify the spin in an axis (v00 in this case) j would increase the spin. Alternatively it would rotate the quantized j rotation in v00 by π/2.
This could thus be interpreted as a spin rate increase or a rotation of the other two orthogonal axes (that is the plane in which they lie) around the axis. j acting on i would then be not one axis rotation,( which i have discussed as producing reflection in the case of a π rotation) , but a plane rotation preserving the relationships on the plane but changing the orientations in the plane in the initial system. Since in XYZ nothing appears to have changed i define this sort or rotation as a relativistic rotation, or more simply a rotation in the initial reference frame.
|
|
|
|
« Last Edit: February 16, 2010, 11:03:31 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #10 on: February 09, 2010, 06:57:03 AM » |
|
So briefly looked at hamiltons quaternions and clifford algebras and some vector algebras and think that these are different to polynomial rotations based on unary operators, and constructed reference frames. I was also pleased to note that although widely described as dimensional this in no way necessitates an alternative to geometrical space. Hamilton i might add is quoted as inventing the term space-time even though it did not have the wide meaning it has today.
The unary operators in a plane, can construct orientation vectors to span geometrical space from an initial orientation. This initial set of orientation vectors is the initial basis, but action takes place through the unary operators sign,i,j,v which are rotations,scalar multiplication and addition et al. This means that rotation translation magnification and reflection are all attributes of this constructed system.
The term linear combination is the nearest equivalent term to my polynomial numeral. Polynomials have a long and important history in mathematical thought and i mean to refer to that in the naming so that one can easily search in the field of polynomials for solutions to particular problems.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #11 on: February 16, 2010, 11:21:14 PM » |
|
So i have made some alterations to previous posts in the light of greater clarity. It is unfortunately easy to confuse what is being resolved by polynomial rotations as the custom and practice seems to be a bit confused with regard to rotations and orientations or directons.
I now have in place notation for orientation and notation for rotators and quantized rotations. It is also clear that a polynomial rotation should have an orientation as a resultant. It is also clear that associations of rotations cannot always be resolved without reference to the orientation being rotated.
Finally to be able to plot these polynomial rotations it is important to know what the resultant orientations are not the association of rotations. As the tables so far have been about association of rotations i will produce a table of resultant orientations and see how that turns out.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #12 on: February 17, 2010, 03:19:48 AM » |
|
A thought that needs development but just noted here.
Each axis has extension and rotation inherent with orientation coming from the axiomatic orientation i0 and rotations i,j,v in planes with orthogonal norms j0,v0,i0. Each norms rotation therefore acts on two orthogonal axes in a plane. Objects in this plane with the same norm will rotate about each others norms depending on the spin ratios: the faster spins dragging the slower spins around repulsively, and if the norms are oriented in opposite directions then attractively.
If the norm of the objects in this plane are orthogonal they will be unaffected as to spin and thus the object will be neutral neither attracted or repelled except by objects with the same norm to their spin plane. these objects with orthogonal norms will tend to have there spin rate unaltered but there rotation around the spin plane norm will be at the norms quantized rate.
Would this provide a basis for action at a distance, that is through spin plane coupling on a resonance type model?
{September 2013 I discover through Norman that Euler has thought this problem through very clearly. However, Norman is the only professor who presents it correctly. Euler rotations as "vectors" double the angles of rotation! You have to use half Euler angles to get the desired angle rotation. The angles here are in fact radian "vectors" or arcs of great circles.}
<a href="http://www.youtube.com/v/0_XoZc-A1HU&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/0_XoZc-A1HU&rel=1&fs=1&hd=1</a>
|
|
|
|
« Last Edit: September 12, 2013, 12:15:36 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #13 on: February 17, 2010, 03:50:23 AM » |
|
| i0 | j0 | v0 | : | i10 | j10 | v10 | : | i20 | j20 | v20 | : | i30 | j30 | v30 | | i0 | i00 | i00 | i10 | : | i10 | j10 | v10 | : | i20 | i20 | i30 | : | i30 | j30 | v30 | | j0 | j00 | j00 | v00 | : | i10 | j10 | j10 | : | j20 | j20 | v20 | : | i30 | j30 | j30 | | v0 | i00 | j00 | v00 | : | v00 | v10 | v10 | : | i20 | j20 | v20 | : | v20 | v30 | v30 | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | | i | i10 | i10 | i20 | : | i20 | X | X | : | i30 | i30 | i00 | : | i00 | X | X | | j | j10 | j10 | X | : | X | j20 | j20 | : | j30 | j30 | X | : | X | j00 | j00 | | v | X | X | v10 | : | v10 | v20 | v20 | : | X | X | v30 | : | v30 | v00 | v00 | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | | i2 | i20 | i20 | i30 | : | i30 | X | X | : | i00 | i00 | i10 | : | i10 | X | X | | j2 | j20 | j20 | X | : | X | j30 | j30 | : | j00 | j00 | X | : | X | j10 | j10 | | v2 | X | X | v20 | : | v20 | v30 | v30 | : | X | X | v00 | : | v00 | v10 | v10 | | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | | i3 | i30 | i30 | i00 | : | i00 | X | X | : | i10 | i10 | i20 | : | i20 | X | X | | j3 | j30 | j30 | X | : | X | j00 | j00 | : | j10 | j10 | X | : | X | j20 | j20 | | v3 | X | X | v30 | : | v30 | v00 | v00 | : | X | X | v10 | : | v10 | v20 | v20 |
A table of the resultants of associative actions of unary operators on orientations i00=i0
j00=j0=i00
v00=v0=i10I have adopted a convention that a rotation produces its resultant orientation when that lies in its plane of operation, but an association of rotations is replaced by its rotational equivalent in the plane. under construction |
|
|
|
« Last Edit: August 24, 2012, 09:24:26 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #14 on: March 20, 2010, 05:53:26 AM » |
|
Without confusion it would seem i can rewrite the orientatobsas i10=i1
i20=i2
i30=i3with similar transformations for j orientations and v orientations. Thus v0=i1. Although i think currently that polynomial rotations are different from quaternions polynomial numerals are not. I can write any quaternion as a polynomial numeral of signal 1 if i introduce a fourth rotation k which can be in any plane orthogonal or not to the three planes already defined. In geometrical space there is no fourth orthogonal plane and so the geometrical analogy breaks down,but the symbolic workings continue in much the same way. What i have to do is set the extension of the fourth rotation to zero, that is only applying to the origin. This gives potential at the origin for infinite variations on a theme all happening at the same time but only being realised when the rotation is given extension in place of another being set to zero. This is very much a quantum superposition, and a case of schroedingers cat! However,orthogonality is not a prerequisite for spanning a space, and so we can have non orthogonal orientations of any number set up in a spanning system for which the underlying symbolic manipulation will be identical,but the geometric representation will show transformation modifiers as in a tensor description. Using Terry Gintz Quasz programme which is bases entirely on hypercomplex math using quad variables. which is to say that each polynomial numeral is a quaternion i have been able to construct polynomial rotations in which the extensions are 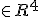 , and then by degrees i have learned how to modify the extensions into elements of 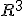 and 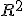 . As i progress in exploring these variaions i will post some image results here. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|


















