|
jehovajah
|
 |
« on: May 13, 2014, 08:15:54 PM » |
|
Reading the Auflage to the second edition is very instructive, moreso than the Vorrede to the 1862 version.
After some 33 years Hermann is able to take a mature look at what transpired to his work.
As you will know if you read the thread
Hermann was beset about by anxieties, pressures indecisions , and saved only by his young mans energy and the determination of his convictions that he had been given a precious insight. He hoped , in vain that his Acadmic peers would see this and grant him a seat to do this crucial work with vigorous endeavour. He published his imperfections his I decisions in a uniquely potent mix of prodigy and promise. He published! And then felt damned!
For ten years he endured meagre response and scant recognition of his work or his abilities. Already struggling to find time and peace ti process and edit his ideas he let this occasional pastime languish. His printed works apart from the few in the catalogues of printers and libraries, mouldered in the warehouse and were eventually destroyed.
But the work was too important to forget, and in particular his brother who was having greater social success than Hermann required this work to be in print to establish the family name, his fathers ideas and his own critique of current philosophy. By his urgings snd discussions Hermann took up the work once more with dedication in bout 1854.
This was the tie Hamilton began to extensively work on his quaternion ideas after critical acclaim had given him a meteoric rise to fame, only later to be dashed by Lord Kelvin and others in a bitter rivalry.
Hermann started nis Ausdehnungslehre again from a different ground plane, Robert insisting that he cater for the mathematical audience rather than the Philosophical one. Thus his choice of the Euclidean format was clear , and his editing choices were guided by formal conventions. With Roberts input and editing as the publisher the work pursued a thorough and pervasive course of Rigorous Euclidean presentations and formats. All areas of Mathemtics and physics and mechanics were accessed by applications of the method.
Much of what was in the 1844 version was completed and extended; new areas were opened up and explored, and the mathematical themes of functions, integrals and differentials were fully exposited and new formats suggested.
When the work was published in 1862 Hermann expressed some disbelief in the work( mostly Roberts) because it bore no relation to the previous, imperfect piecemeal inconsisten mess he had published earlier! However that was at least his own work!
At first forv5 years it looked like Roberts plan was not working. But then in 1867 Yänkel published referring to the ideas in the -Ausdehnunglehre and the floodgates opened . It seemed as if they were waiting for Riemann to die. But more astonishingly for Hermann was the growing fan club for his 1844 work! It served that the more insightful realised that the 1844 publication was the bible to refer to! As. Consequence Hermann was able to afford to get the original work reprinted with notations, eagerly snapped up by a hungry readership. There was even talk of a colour pint edition!
Hermann list several key advances in his method made by insightful others like Stregel, but Leo his own advances made by inspirational retreading of his seminal work as a young man.
There are about 4 papers he mentions including this one on Hamiltons Quaternions. Plus he mentions and insightful review of the meaning of his Ausdehnungslehre, perhaps in distinction to Roberts, no also started publishing on the topic.
By 1877 Grassmnn was making plans to further develop this work, started in a occasional and piecemeal way; published full of imperfections in hop, dashed, snd finally completely redacted in collaboration with his brother, launching him into a celebrity he could not have dreamed of! and then he died!
In keeping with his absolute fearless clarity Hermann points out where his work was fruitful, unfruitful or even inconsistent! The work clearly was a work in progress, but it's deep I'm was to supply the modern Mathematicin, physicist, engineer and mechanic with a deep understnding of the melded connectedness of all the rapid and confusing modern developments in scientific and computational and geometric thought.
Those that valued it most were those whose philosophical natures lead them to try to understand how this modern burgeoning intellectual growth was deeply connected to each and every technological and material advance in understanding the space in which we live and of which we are composed.
There is a deep melded harmony in the way we interact with space in the sciences nd engineering and Grassmann drew attention to it through what I call Spaciometry, and the effective labelling of it nd our processes in it.
|
|
|
|
« Last Edit: May 01, 2017, 07:14:34 PM by Sockratease, Reason: Apostrophe Removal »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #1 on: May 19, 2014, 10:46:39 AM » |
|
Whenever I read summary biographies of theoretical physicists or mathematical engineers of the late 19th early 20th century, those who are now regarded as pioneers are always said to have created their own, idiosyncratic vector algebra. This is so of Heaviside and in this particular instance P.A.M. Dirac whose bra-ket notation is regularly inflicted on young impressionable minds.
I suppose it is easier to make such statements than it is to delve into the murky and nefarious misdeeds in academia!
Vectors in principle as I now understand are inherent in the ancient Greek notion of a segmented line, especially as described in the Stoikeia and elaborated on by Apollonius and Archimedes. Many Pre Socratic philosophers from Thales, Herakleitos , Parmenides Luycippius and Democrites, considered the plenum to be eternally dynamic, and their drawn lines just to represent instaneous form or motion,: skesis or sketches and schematics of ephemeral manifestations in the flow of Rhea or Hekate. Phusis was that grand system of opposing entities which alone maintained a sensible equilibrium or a system of equilibria with an attendant Harmonia. These two were represented as sisters and members of the 9 muses, the attendants of Apollo the great Sun God whose beauty was admired by all!
Nice myths, and memorable stories, which in the absence of television game shows occupied the minds of young impressionable people of the time. Now these myths reappear in some detail in the console games loved by do many of today's youth.
To the wise they encoded deep philosophical truths, and Newton as an example devoted considerable effort in his youth to deciphering the physical and alchemical information encoded therein. But the line segment as a symbol belongs to the Pythagorean Eudoxus, who encoded the understanding to be found in the mosaic arrangements that decorated the Pythagorean temple walls and floors. These temples to the Pythagorean Muses were called Mousaion, whence we derived Museums and also the epithet mosaic. But ib Euclid these patterns are called epipedoi, and in the literature speripedoi. They were also called Epiphaneia, because light fell upon them and cast shadows. These shadows were marked ti designate certain times of the day or year, and so crazy "abstrac" patterns were noted in early examples of mosaics.
Eudoxus took these principles to the Pythagorean conclusion that all forms can be reduced to these dynamic shadows cast onto these mosaic floor patterns. The shadows could be quickly sketched round thus giving grammai or drawn lines in the earth. The embedded pebbles, later baked tiles enabled these lines to be counted or measured, and this was the meaning of geometry.
Geometry used these drawn lines on mosaics to measure space out to the sun, and the stars, and this was known as Astrology. Thus geometry was not about surveying the earth, rather the earth was measured to survey the stars and planets in their motions and positions .
Aristotle who through circumstance never completed his Pythagorean studies under Plato, investigated this dynamic relationship between all things that moved in his great work on metaphysics. His ideas were greatly influential on Islamic scholars and notably on Newton and many others. However they were criticised by Gilbert in his work on Magnetism and on the empirical basis of human knowledge. In this Gilbert predates Bacon, who somewhat witheringly disparaged Gilbert's great insight.
Suffice it to say Aristotle was misleading on many many points and was taken with a pinch of salt by many later philosophers, who found safety and clarity in Euclids Stoikeia. Later some questioned even Euclid!
But it must be acknowledged that in Newton all that was best in Aristotles reasonings were combined into Newtonian astrological principals, ie the Principia Mathematica. Thus the Greek notions of dynamic line segments pass on to Newton and others who following Archimrdes, Apollonius and Parcletus, to name a few , gave us a system of analytical Mrchanics. However it is Newton who combines this with the analysis of Aristotle on motion to give to us the new Mevhanical philosophy that avoids many of the ancient extremes and mistakes..
From this source most of the scientific clubs and societies in the world drew their concepts of how this world order might best be described, and what mathematical principles might best be employed in doing do. Buried deep within this apprehension was the ignoble line segment and it indissoluble link to mosaic ratios of line segments and to Eudoxian proportions. Amongst these line segments and mechanical motions of drawings, the ubiquitous circle was also preserved, and its utility and fundamental constructive power was seen as the ultimate goal of all analysis. It's perfection could hardly be described without all it's children of which the most important was the segmented line.
Notions of straight, parallel and rotation were fundamentally and mechanically defined in terms of the circle and the rigidity of space. Even though it was impossible to find such a design in nature yet it easily dropped out of rotating every rigid object no matter how convoluted! Eudoxian proportions fundamentally rely on it, as do geometric extremes and means.
Thus the great secret and harmonium Mensurarum of Sir Roger Cotes, that which Newton intuitively perceived, and De Moivre also skilfully analysed both in trigonometric form and probability measure form is the unit sphere and it's projected shadow the unit circle.
It is the unit circle which defines every aspect of the notion of line segments and thus every spect if the notion of so called vectors. And while Newton addressed these properties in his geometrical reasonings, yet he did not make fully clear the underlying Algebra. And While Hamilton by brute force extended the underlying algebra into 3 dimensions from his noteable concepts in his essay on the science of Pure Time, that is conjugate functions or couples., it is remarkable that he did not fully apprehend what he was pursuing so ardently.
On the other hand, both Lagrange and Euler casually cast these things about as if they were playthings, but it is not certain that they grasped the fundamental nature of what they had adduced to Newtons great works, nor those of his acolytes De Moivre and Cotes. In any case they did not seem concerned to fundamentally give insight into how these things may be best understood.
This fell into the hands of a great an innovative teacher named Justus Grassmann, who was charged with the responsibility of bringing the academic standing go the average Prussian child to the level required for Prussia to compete with the French empire in the modern industrial world. Indeed it was the duty of all educators under the imperial seal to implement the Humboldt reforms throughout the length and breadth of the Prusdian holy roman empire.
As such, the classically trained Grassmann, educated out of the best of the French Ecole tradition, which was principally disseminated by Lagrange from Berlin, who saw to it that Legendre and the work of many others became the text books in Prusdian higher education; as such Grassmann deconstructed the work of Legendre who himself had reconstructed the works of Euclid from what sources he had. This lead Grassmann into a deep logical analysis and synthesis, that resulted in him training students in a constructive and dynamic geometry, which he could show logically hung together and underpinned Aruthmetic. Rather he was keen to show that arithmetic was the fundamental of all geometry! But he came unstuck at multiplication. Under his analysis there was no logical precursor or analogue ti multiplication. It stood in its own right as a purely geometrical construction!
In fact, in my opinion, this was a misreading of the concept of logic, perpetrated by Aristotle. Aristotle based his definition of logic on the grammar of language. While tis is a very powerful consonance it is also a fundamental dissonance. Language in the end is a verbalisation of non verbal experiences. Much of what is communicated in language is non verbal, and that means it has a referent in one or many of the other sensory modalities. Thus to understand language we have to start in the nonverbal experiential modalities. This means we have to start in our experience of interacting with space.
To cover this concept I defined the notion of Spaciometry. This covers an individuals logos, analogos, sunthemata and summetria response. These non verbal interactions with space underpin the comparison, distinction and declarations of those distinctions we call language. Thus multiplication is without doubt a non verbal primitive. In fact I claim we have mis apprehended the primitive by calling it multiplication!
In any case this intense scrutiny and synthesis lead to Hermann developing a unique constructivist approach. This Förderung was so innocuous that it literally requires the individual to go back to the wide eyed suspension of critical faculties common among children. This concept is expressed in 2 Laws of Grassmann
AB=-BA
And AB+ BC=AC
This is the fundamental product sum laws( nb! Product sum not product and sum) of what Grassmann called his Aussere product.. The inner product is based on a different kind of line segment, what I have called the trig line segments. This produces a " Normal" or usual product but the product sim is still Grassmanns product sum law.
This product sum law makes no sense as a measurement, but as a process description of spatial behaviours it is absolutely fundamental to any algebra of space.
None of this was notated as precisely as this. In fact it was not even considered as needing notation because it was sufficiently clear in the rhetoric of any geometrical " proof" or exposition. The fact that Grassmann set out an algebraic notation for it, which is really a symbolic arithmetic for it, is one of those rare moments of wacky thinking that just proved to be so right! Recall Bombelli saying that his idea of adjugate numbers was so crazy he had to shut his eyes and muddle through! Again this was described as Akgebra, by Bombelli. As you will read in the links in the thread on Bombellis operator, if they are still active, Bombelli went on to solve quintic and degree 6 equations using his notational algebra.
This of course begs the question what is algebra? Newton hated the idea of notating all his muddled thinking by means of these symbols, but Wallis believed this could help others to emulate the genius of the very best mathematical minds.
It should be noted that despite protestations to the contrary algebra represents muddled, muddied and contortional thinking in feeling ones way to a solution. Often it requires one to assume the impossible or the unexplainable, to hold ones breath or shut ones eyes and hope to god it all works out and cancels to some easy result.
It is a tortuous exercise which only a few actually enjoy. In particular, the great savants who could calculate pi in their heads to several hundred places would find the formulaic patterns intriguing and even " nice"! But to the vast majority of us these algebraic symbols and patterns are literally " all Greek" to us.
So I say that the Algebra that Grassmann and Bombelli perceived is a symbolic procedural algebra best expressed as rhetoric. Although this is much longer to read or explain it is more user friendly. The best communicators explain the symbolic arithmetic with inviting analogies, as I remember Lancelot Hogben doing in his book Mathematics for the millions, which I read as a child and which confirmed me in my decision to become a " great" mathematician!
As you see I failed in that goal round about entering into university, when my relatively sheltered mathematical training was introduced to the harsh realities of pontification! No one would explain how all these mathematical symbols and juggling actually came into existence and had any relevant meaning in everyday life. I was astute enough to realise that my mathematics should be able to describe a door! And yet I could not describe a door mathematically.
The Grassmann concept of line segments as the basic primitives of an algebra is so far reaching that you need to see how it reaches into the mind of Dirac to realise this. You need to ubpnderstand that Hamilton recognised Grassmann as a Master, that Gibbs recognised the work ofbGrassmann as fundamental to replacing the arcane Alice in wonderland world of Quatenions, that Heaviide realised that Grassmanns principles properly understood gave him physical insight, and that Bill Clifford determined to spend his life promoting Grassmann work and analysis.
Today Norman Wildberger, David Hestenes and others are busy continuing the programme and work of Grassmann. Of course Grassmann is dead, so why name your work after him! In all fairness Grassmann is referred to as the source, but few really explain how much what they discover by using his methods of Analysis and synthesis has already been written down long ago by Grassmann.
In this thread Grasdmann deals with his issue in that particular instance of Quatenions. He does not clim to have discovered quatenionic, but rather that what can be discovered by Quatenions can more rapidly and more cogently be discovered by his algebra, and indeed already had bern by him!
<a href="http://www.youtube.com/v/myxx2uaqPLM&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/myxx2uaqPLM&rel=1&fs=1&hd=1</a>
By the way Grassmann fully credits the works of Lagrange and Euler and others as his inspirations.
|
|
|
|
« Last Edit: May 01, 2016, 11:46:41 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #2 on: May 21, 2014, 12:53:49 PM » |
|
<a href="http://www.youtube.com/v/H8xBlLWdzBE&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/H8xBlLWdzBE&rel=1&fs=1&hd=1</a>
<a href="http://www.youtube.com/v/GMZoXXaOFeQ&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/GMZoXXaOFeQ&rel=1&fs=1&hd=1</a>
These 2 videos are preceded by 2 more that I recommend watching on Galois theory.
The work of Gauss is often difficult to place in time due to his reticence in publishing his half formed ideas. Thus he later would sardonically. Liam precedence to any published or prepublished work tht he reviewed if they contained ideas he had explored in his " notebooks!" . In fact his students continued this trend after his death often climbing intellectual priority. Only the most capable mathematicians like Hamilton, would resist such fanatical domination of mathematical thought.
It is instructive however how the ideas testify to a sort of Zeitgeist and commonality of thinking. It must be remarked however that the intellectual climate, despite the difficulties in communication, relied upon frequent and lengthy scholarly missives and letters , often hand written , but later published as memorie. In addition, true " education" in the classics required travel to the great academies in Europe, in Baghdad and Southern Spain, and infrequently to the monastic centres in the Orient. Thus Libraries and manuscripts were of invaluable assistance in transmitting wisdom and intellectual philosophies around the world, wherever traders and merchants might ply their trade.
Gauss was impatiently ambitious, wishing to make his mark as one of the great Prusdian intellectuals. Up until then, the French Evole dominated the intellectual curriculum of Europe.mfiercely patriotic Gauss wanted to deliver a sense of homegrown greatness to the Prusdian Empire, which until then imported all it's intellectual capital. The royalty of Rurope in thir meetings often boasted of their national prowess by these accomplishments. In Prussia and Russia it wasa great royal embarrassment to have mainly peasants as the main economic power, whereas the advancing industrial nations boasted of mechanisms of thought and ingenuity. Engineers and mathematicians clearly as inventors had transformed the economic status even of small islands like Great Britain!
The Humboldt reforms in Prusdia were not a luxury, they were a geopolitical necessity, which all intellectuals in Prusdia acknowledged.Gauss seems only to have concentrated on the Academic quality of the higher institutes.
What I have learned from Grassmanns Vorreden and Auflagen is that their were places of rich intellectual and cultural commodity. Stettin( Sczeczin) was a dormitory community to such an area in the Rhone valley. Thus the intellectual thought of Rurope flowed into Stettin because the printing industry had taken a major advance in this area of Prussia texts nd folios books and manuscripts were all accessible if not in the libraries then hot off the presses in Leipzig. Justus Grassmann hermanns father , and Robert Hermanns brother ho lived with his father, whereas Hermann lived ith and was fostered by his uncle, we're extremely well read.
By all accounts it seems that Hermann was a late developer, probably due to a kind of autism and fragile health condition. Thus benefitting from the education system in Stettin that his father Justus set up required Hermann to do a great deal of self or private study. In this way his Förderung was developed without harsh academic correction . But it also meant he was unaware of certain standard ideas in the public domain. For example he had only heard of Möbius Barycentric calculus, and only read it after he had formulated his point algebra as I have called it. Again Gauss tentatively published his ideas on what are now called Gausdin Integers in about 1831 after being persuaded by Wessels paper on directed magnitudes that his use of imaginary numbers, though metaphysically and philosophically unsound in his opinion was somehow fundamentally important.
Gauss used the Eulerian i notation extensively and arguably in a way that defines it as a complex number adjugate, following Bombelli. It is not clear if Euler got beyond viewing i as an ratio which was its own negative inverse which passed beyond the infinite unbounded ness of space to return on the other side! However he thought of it, he states in his institute on arcs and integration that he could see a way through the problems of understanding the solutions to certain equations only this way! He was considering polynomials we can call circular functions, and it resulted in him linking i indissolubly with the arc length through the trig functions. It is hard to express how this notion found only in Sir Roger Votes Eork some decades earlier came into his imagination.
So Grassmann states in the 1862 Vorrede that he had not known of Gausdian integers until after his publication of the 1844 Ausdehnungslehre. He took it as a sign that he was on the right track because the Gausdian form was an example of his general concept of an Ausdehnungsgröße.
From the videos you can understand that the Schwenkunlehre of Hermann Grassmann was arguable extant in the writings of Lagrange and Lplace, and certainly in the concepts of Ruler. Thus what I have called a Grassmann Twstor is not uniquely Grassmanns. In fact I clim now after studying the Vorrede of 1844 that Grassmann goes out of his way to make plin he claims no original thought beyond his Förderung! His mindset was totally unique and insightful and it was this mindset , this Förderung he was at pains to Promote as a method of analysis and synthesis utilising " algebraic" conventions.
By 1877 the concepts of ring and zgroup theory were firmly established in Europe as the basis of modern Algebra. In that regard, Hamilton is often hailed as the father of modern Slgrbra as a separate discipline. However as Leah's, these things are not so clear cut. Along the way many Europeans contributed to what later was gathered into the new subject domain called Algebra. This was not without a considerable academic turf war in which many reputations were made and lost! Hamilton himself became a casualty of an international backlash against the new algebras.
My opinion on numbers stands. We are better off without the convoluted concepts they have become. Instead we are better off adopting the iteration of applying spaciometric Metrons to space and singing the counting ong as we fo so! The world will be a much happier place!
One note. Often mathematicians will tell you it is impossible to trisect an angle! This is not true. If you press them they will backtrack and mumble about rulers and compasses.rulers and compasses are mechanical devices , pragmatic tools for constructing the forms which geometry then idealises. Newton firmly based geometry in an interdependent loop or pair of loops with Mechanics. There are many ingenious mechanical devices that can precisely trisect any angle!
However what is perhaps more Pythagorean in constructing this trisection is the ratio of circles. Whatever pi may or may not be we can construct circles in my ratio by their diameters or radii. Thus to mark of the third of any arc is not only possible but mechanically simpler than constructing a perfect straight edge! In fact once a circle has been created as a disc it is a curious fact that the hypo trochoid of a disc inside a circular wall in the ratio 1:2 is perhaps the best way to trace out a perfectly straight line using the disc centre. All other concepts involve defining a straight edge to define a straight edge. This convolution or tautological reasoning will iterate to a perfectly straight line over time, but a circular method is faster and more accurate.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #3 on: May 26, 2014, 01:45:13 PM » |
|
So I get deep into the Fourier transform as an example of a Grassmann tisyor( see thread on twistor) and I am close to analysing light and magneto Thermo electro complexes as twistor complexes. But the detail is distracting.
What lifts me up out of the potential quagmire is the glistening rotating sphere of unit radius. I have seen this sphere many many times, especially in the thread on the fractal foundation of mathematics, and I habpve even called it Shunya, the source of everything to do with measurement. Shunya is indeed the Sanskrit for the fullness of everything, so the sphere is merely a representation a metaphor.
My meditation on the V9 group or possibly a ring has slowly deepened. I made the mistakes of rushing in on my thread on polynomial rotations. Understanding these product tables / matrices ( Cayley) is hard, that is interpreting them. The V9 group table can be rolled up into a torus but what is the best way to do that? A square table gives one result, forming the products into a hexagonal shaped table by judicious cutting gives another.
The physical significance then takes on if fervent interpretations with regard to the flux of vortices in space!
Again the unit circle/ sphere is involved in apprehending the spatial significance of the patterns counted. We lose sight of this by replacing Arithmoi by Numerals.
Rotation is fundamental to my thinking process and my experience and crops up everywhere, so had I understood Hermann correctly, was he seeing what I see everywhere?
So many of my insights into rotation can be linked back to him one way or another. Was I right about the cyclical rotation? And the inner product, does it behave like normal integer multiplication?
The place of Hamltons Quaternions generated more questions as well as insights. Thinking about it I realised that a better working title is " How to find the spot where the Quaternions are in the Theory of stretchy thingies!" it is quite complex, and Hermann goes into detail. Complex as it is he has not yet used complex numbers! Rather he has used cyclic rotation !line segments and cyclic rotation of the indices. What effect foes that map to in space? It is not a simple rotation, but a convoluted one.
I was right to go slow. Hermann has grasped rotation only partially. That is in keeping with his times, the full extent of rotation eluded them. Rodrigues and Hamilton were the pioneers of an understanding of 3d rotation. Hermann was not. However what he was was the instigator of a method that could build models of any kind of spatial process that had the properties of three types of group or ring products and product sums.
It is instructive to see how he characterises the 1844 Asdehnungslehre as the analytical phase of his work, and the 1862 as the Synthetical phase of his work. Thus he shows now as previously that Quaternions are a combination of products in his algebra, particularly the 2 main products: the inner and outer products.
We lose sight of the spaciometric analysis as Grassmann has chosen a more formal format : that of the Eclidean or as23 call it nowadays, the Axiomatic format or presentation of Ring or Grouo theory on the n dimensional unit sphere.
However, because it is the unit phere it is all about Ritation, and cyclical Ritation is Grassmanns key tool or apprehending and finding his way about in this lineal segment space!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #4 on: May 27, 2014, 12:02:25 PM » |
|
What is abstract thought?
I claim that it is a misnomer for Analogous thinking. My understanding of analogous thinking starts with the Babylonian cuneiform tablets. This is the oldest script that we can decipher that represents human thought clearly making analogies. However it is my suspicion that the Harsppan and Dravidian, Indus valley civilisations represent an even older civilisation capable of analogous thought.
So the sphere , the cone, pyramids a and cubes are analogous to what exactly? These often are considered as pure abstractions of thought . I am convinced that they are perfected analogues of structures found all around us, where perfect here means constructed by rigid adherence to an integrated process by a human mechanism that itself is rigid or constrained.
As a process which is found in our environment, sequential actions and behaviours are exhibited in our subjective processes, but these occur recursively at all scales. The result of this self similarity is almost self similarity at all scales! Where we " perfect" this relation is precisely where we are incapable of distinguishing any difference. Thus our standards of comparison, contrast and distinction, the do called by me Logos Analogos response is based on the principle of exhaustion! I can apprehend no smaller difference, nor any difference at all in that which I call identical or perfect in fit!
However, in reaching that determination by some recursive , that is iterative analytical process, what do I call all the nearly or almost similar forms if not Analogues?
So it is that Grassmann great contribution to human mathematical and Scientific thought is to raise the level of analogous thinking to that of a fundamental cohesive form of analysis that generates inspirational comparisons and contrasts in a consistent procedural manner. In doing so he draws on some of the most general thinking of his times which later develops into Ring, Group and Homotopy theiry.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #5 on: May 27, 2014, 08:45:02 PM » |
|
The quintessential example of analogous thought is in my opinion expressed by Eudoxus in books 5 and 6 of Euclids Stoikeia. The thought is clearly carried over into book 7 the folio on the Arithmoi and the definition of Monas the .concept of unit Metron.
It is of significance that every term used in the fundamentals of group or ring theory derive their meaning from Euclids Stoikia and these 2 books in particular. Analogos is defined or exemplified at the outset as is homologous and Ido Morpheus etc. thes concepts have their origin in Pythagorean philosophy of which the Stiikeia is merely an introductory or undergraduate course!
The notion if measurement by counting a Metron is established in a kind of dance in which a Metron is laid down in a contiguous pattern. This concept of a Metron is sharpened to the concept of a Monas, which is a standard Metron unit. It is then that the process of factorisation is formalised by the so called Euclidean Algorithm and the Arithmoi are identified, defined and distinguished. This is in book 7 where the notions of artios ( perfect fit) and perisos( approximate fit) are carried forward from the concepts in books 5 and 6. Into the Namespace from which the various types of Arithmoi are named.
The proto Arithmoi deserve particular mention in that each one represents a type of product, the progenitor of a multiple form that cannot be achieved by any other means.thus the name prot which usually means first . These are the first or initial forms of a whole series of multiple forms. It is the algorithm that exposes these multiple forms and which drives the naming of them.
But the concept of multiple form derives from the previous work of Eudoxus in Books 5 andv 6 which in turn is his deep meditation on the mosaics in the Pythagorean Mousaion or temples of the Muses.
So while unit is not defined in books 5 and 6 it prepares the ground for its conception. In a sense books 5 and 6 are a more general discussion and introduction to the principals of comparison, and thus a more " algebraic" introduction. However algebra is an Arabic word and Eudoxus treatment is rhetorical , conceptual and reasonably direct. The things he refers to as magnitudes are symbolised by a line segment or a form. In this sense it is symbolic as Algrbra is symbolic , that is it uses symbols to rhetorically discuss its subject matter.
Because symbols are used we may justifiably ask to what they refer and the answer would be twofold: a quality called magnitude in its many and various forms; a quantity of a specific magnitude. But when pressed to explain quantity and how it differs from magnitude it becomes necessary to define the concept of unit so as to be specific.
In general however, we do not wish to know specifics of quantity but rather how quantity behaves vis a vis another quantity against which it is compared. It suffices to know that one is a multiple form " of" the other either directly by being of the same qualitative magnitude, or indirectly by occupying the same quantitative space as an identical form which may be of any other quality.
In fact, the behavioural dance is the same regardless of the quality of the Metron if it remains true to the form of the Metron that is appropriate to the quality of that being" measured".
Rather than labour the point suffice it to say that the Pythagoreans would use any appropriated form in their mosaics of whatever material or roughly similar size. And yet each form would be counted " as one". Counting as one is by no means implying that the form is a unit! Our behaviour in counting in this way is not to measure but to perhaps remember or encode, if not for the pure pleasure of recounting to others some conception of multiple form.
The introduction of the Monas therefore signifies the introduction of the standard unit. But we will find in higher Pythagorean philosophy that this unit represents all that is! In this regard the Monas as the Uni-verse is equivalent to Shunya as the fulfilment of all or as everything. This it is a thing to note how Shunya becomes 0 or nothing and yet it's equivalent Monas becomes 1!there is a history behind this, that as usual involves human frailties!
Yet it is also tru that the Indians used Ek to mean the initial count just as the Greeks used en, so we must distinguish the cultural iterative name from the overarching concept they are related to.
It is therefore important to note, that Grassmann as a young man and articulately as an admirer of Hegelian logic or rather dialectic process has these concerns infusing his mind at most levels. The rise of the more philosophical treatment and debate about the ultimate rationality of human thought being expressed in the works of the Mathematikoi, as Plato owned, and the church fathers hardly contested because they could not , also fuelled the lifelong efforts of some to establish their opinion.
Roughly Kant put it tht human rationality was discoursive, that is given by divine intervention and revelation, and the sublime nature of Mathematics, principally the Principia of Newton, established his contention.
On the other hand Ficht and others contended that mathematics was the work of mans heart and mind, constructed by applying the mind in rigours of logic and deduction based on propositions expositions which relied on very few " axioms".
Such Axioms may be of divine origin but the rest was the " handiwork" of human ingenuity and genius. The implication was that the claim that rational thought derived from god and his " logos" was either over stated or entirely false! If false it left an entranceway for men of science and engineering to claim they built and added value to the world in which they lived. Further their towering intellect was equal to the task of taming nature!
That being said Kant sought in mathematics evidence of Transcendence, that which was beyond human capabilities, while Ficht in particular sought to demonstrate that all of mathematics to that date could be constructed.
For the general person it hardly mattered, because arithmetic was not questioned, but rather used as a model of human constructed calculus. But for Many intellectuals it was troublesome as to where to locate the source of this construction. Abel for example demonstrated a deep axiomatic group structure on the ordinary counting process., which suggested a psychological base to our conting and mathematical concepts.
Justus Grassmann took this further constructing a logical or a ground in logic for the synthesis of Mathematics. It is in this family tradition that Grassmann pursued his fleeting analogy between displacements and the arithmetical sum of 2 summands. This is how he started his analogous thinking, with reference to a product and to a sum.
What I find in his writings is not the initiation of yet a new innovation, but rather the working out and working through of the idea glimpsed so simply. It took him years of effort and Analydis to check if his IDE was "right" or rather consistent. This work of reprocessing all of the then known mathematicians to see if his idea still worked meant that he read extremely widely and persistently. He deconstructed eveything and reconstructed it according to his new principles sndr ideals. As he did so he naturally absorbed the mathematical thought and conventions of his day.
What I now find in this piece is a full acceptance and use of common mathemrucal notation, which is then deconstructed and analysed and reconstructed either as is or in a new more efficient way. Atthe heart of this resynthesis is a derived notion of the unit . This unit is a Monacical system or Einheit. These quantities in a Einheit are line segments usually and instructively set to 1 or unity. This unity then is fed into unit lengths, unit values. Allied to them are coefficients and these conceptually are Tallies or counts of how many unis.
But then , along with his contemporaries he can change these coefficients into something called a number, and this can be real or imaginary. He does not criticise these " numbers" but simply takes them on board.after analysing them as Euler did, but concluding they had an analogous and consistent geometric interpretation.
Wht I see then is his careful and extensive use of verified analogy , adjusted analogy to make the notation work mnemonically, and recursive analogy. Once he has analysed any analogy and seen how it works he then constructs a detailed working model which represents spatial interaction. In the process of doing do he often sees where a mistake or a misapprehension has occurred in some conventional theory and corrects it.
So it is with Quaternions . His method deconstructs all spatial interactions into 3 main product groups. From these he can instruct the details of any kind of product.. Finding an author who brings to the tabs the Quaternion principles and products, Grassmann is immediately abe to show that these products, far from being " new" to hom were in fact discussed at length in ome pares dealing with general products in his Ausdehnunglehre.
The upshot of this is he can deconstruct the quaternion Algrbra into its fundmental lineal algebras in an hithertoo unheard of analytical tour de force! Not only that, but he can point out misuses of the Quaternions, and show the correct or best algebra to use in those circumstances.. Not that he is boasting because he cites those who have given the better treatment of a problem using the style of Algrbra he advocates.
He shows an ability to derive the form of algebra suited to the nature of the problem , all of which he demonstrates in detail making reference to the analogous thinking method he utilises to get his result or formula..
I have yet to finish reading the last third of the article, but already he suggests that Quaternions best role is in Sperical Gometry and trigonometry. I know for a fact Hamilton applied it irst their to great effect!. Thus it is becoming clear that the mastery of his style of thinking is of great advantage to a more fundamental pprehension of how I, and geometers and astrologers in general might better interact with space when it omes to applying Metrons and counting!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #6 on: May 27, 2014, 09:48:34 PM » |
|
<a href="https://www.youtube.com/v/saWxZs2Xo24&rel=1&fs=1&hd=1" target="_blank">https://www.youtube.com/v/saWxZs2Xo24&rel=1&fs=1&hd=1</a>
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #7 on: May 30, 2014, 03:31:41 AM » |
|
Hermann now concentrates his mind on the spherical trigonometry of the unit sphere.
He starts generally showing how to construct a set of line segments that represent any polygon on the surface and hw to construct Polarecken. From these he is able to apply some combinatorial rules referenced in the 1844 and 1862 Ausdehnungskehre which in effect label all the possible relationships. Thus I perceived that without specifying the details he had handles for every possible configuration of the system.
The rocess then was simply to assign details to every handle and this appeared to be done in long chains of proportionalities. .
Several substitutions allowed him to generalise certain corner angles and thus deal with spheres that were not units.
Applying the fundamental or Msin products allowed him to identify groups of orthonormalisation radii which then allowed him to create a quaternion easily.
Further he goes on to derive special cases for polygons of any number of sides.
In his treatment it is quite clear, although notationlly intricate, that Quaternions are most easily understood in terms of spherical trigonometry where no complex numbers are necessary.
In every sense this is the conclusion I came to in the fractal inundation thread, that numbers are underpinned by a more dynamic magnitude, the trigonometric ratios.
This understanding really means to me that numbers as such are not entities in themselves, but rather symbols for a set of relationships between line segments in space. But the curious thing is these relationships exist within the sphere, and when yo unravelled the sphere by Eulers - Cotes formula and radians or Chords, you can construct curves of any frequency that sum to any form or surface by combination. This is the deep relation of the Fourier transform as it applies to bound forms of any quantitative size.
In passing I again make reference to the principle of exhaustion . Commensurable algorithms are done to the best of our ability, and that in an exacting standard is until we drop from exhaustion. In Latin or Italian Finito means finished or completed. Infinitum means not completed and ad infinitum means to the uncompleted end! Thus ad infinitum, usually translated as an infinite process means only an exhaustive pricess which ends incomplete.
The binomial series expansions are thus incomplete expansions. Euler's expansions are incomplete expansions. To assume otherwise removes us from Archimedian and mechanical principles into the realm of fantasy.
Cantors infinities are thus fantasies. The difference in pricess he experienced is merely the difference in magnitude we all accommodate between a formal line and a formal plane and a formal volume. To call these all different infinities adds little to the realisation that they are different magnitudes!
Our most useful conception of number is to be found within the trigonometric and related logarithmic tables, which ski ground our basic notion of function. Looking at it that way enables the spaciometric mosaics , the Arithmoi of whatever form to assert their fundamental place in our interaction with pace, and our systematic proportioning. Our calculus then can be understood as the analyss and synthesis that it is and not as some arcane symbolic device.
It becomes increasingly clear that in Hermanns time Euler, Lagrange, Aplace,Gayss,and Fourier were looking for generalPrinciples of application of the mind to engineering and philosophical issues.It so happened that in Mathematical symbols they could encode such processes and demonstrate their efficacy. So it is not out of time that Hermann hold propose his method of Anslys and synthesis.. What is striking is that his nonsensical method should in fact be the way to handle this specific approach to spatial interaction.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #8 on: May 30, 2014, 11:15:46 AM » |
|
An aside: this video game person ( http://www.terathon.com/lengyel/) has a fair number of talks/papers using the works of Clifford and Grassmann. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #9 on: May 31, 2014, 11:44:29 AM » |
|
Thanks Roquen! And welcome to the thread.
What may seem an aside to you is in fact an on point response. I find that reading Grassmann in any of his articles or works generates such flashes of insight and connection that his name is now almost a meditative Mantra!
My labour is to clear a way for everyone to see the most useful mathematical method ever constructed, but also to make it clear that it was not constructed by some incredible genius, but rather a young man, struggling with a kind of autism, and various health problems whose father was too busy to devote the time needed to care for him. Thus he was brought up by his uncle, and away from the academic pressures within his own fathers household.
Although they were a close family Hermann was definitely not considered to be the brightest of Justus Children. Nevertheless he was given a gift by God, he believed, an extra insight to compensate for his difficulties, this led him, step by step to shape his education in a particular way that no one else had been able to do. This insight is a childlike view of spatial relationships. Clifford was so struck by how elementary or babyish it was that he remarked How much it was like Alice in wonderland or even Jesus admonition about entering the kingdom like a little child.
To be sure it is rigorous and demanding requiring a flexibility of mind and a broad mathematical education to see the full beauty of it. Even Gauss was put off by the flood of new and innovative ideas expressed in the 1844 text. But the essential idea once seen is so simple that you know it is special and almost universal.
For me Mathematics has been revealed to be a sham subject. It has a place as a subject only in a larger setting which directly is computational science a subset of computer science! Bertrand Russel attempted to embed it in Philoophy, but went about it in a way that AN Whitehead thought would resolve the issues that actually failed to. The point here is Whitehead was a Grasdmann Enthusiast, but he failed to understand Grassmann properly.
The difficulty seems to be the confusion between Platonic dialectic and the more modern Hegelian dialectic that Grassmann fell in love with. The 1844 version was an abortive attempt to present both his idea of a fundamental " algebra" of space and Hegel's fundamental philosophy of all that is including that which is contradictory. Hegel's dialectic forces the mind to work though and resolve contradiction in a new whole, rather thn to ignore or hide oneself away from it.
There is a " truth" that is within and or around all contradictions that resolves the issues at different levels. When this mindset is employed a fractal complexity emerges requiring us to iterate continuously to see or experience all that can be experienced at any level.
None of this would make as much sense if the computational sciences and the computer since and technology had not employed these ideas to wonderful effect in re presenting our sensory experiences to us through the digital media both on screens and on speakers and now in haptic environments.
Grassmanns analytical and fSynthetical model is so apt for the computational sciences that it is no wonder that they have adopted it at the highest philosophical levels of their craft.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #10 on: June 01, 2014, 09:42:19 AM » |
|
I spent some time translating and meditating on the first stanza of the Stoikeioon book 7. This was why I highly doubted the myth or false story about the Pythagoreans being in crisis when they found 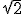 was in commensurable. MonasThe story goes that the Pythagoreans believed there was a fundamental unit from which everything was made. Thus like Leucippus and Democrites they believed there was an atom, that is an indivisible unit of matter from which the material world was constructed. This misrepresents their philosophy grossly. The Pythagoreans defined the concept of Monas. This definition is as general and process oriented as it is possible to be in any language! That it is presented in Book7 of a undergraduate course in Pythagorean Philosophy written by the Euclidean Platonic Academy indicates that it is not a fundamental notion , but rather a constructed notion based on a priori primitives and practices which are more fundamental. Thus the first 6 Stoikeia are fundamental primitives to ANY notion of Monas. Thus it is with great delight to read Grassmanns opening words to this article. The Ausdehnungslehre makes the Monas ( properly grammatically it would be Monad in this position in a sentence) an arbitrary Assumption! The concept of a unit is completely arbitrary! In the method of the Ausdehnungslehre! At a deeper or more primitive level that means that the unit sphere is an arbitrary concept. |
|
|
|
« Last Edit: June 01, 2014, 09:52:17 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #11 on: June 02, 2014, 01:06:43 PM » |
|
It is clear, from this standpoint, that the Arithmoi on which the concepts of number are ultimately grounded in the west , are an arbitrary concept, in line with the Monas, the unit identified as one , that is its counting name is " one" ; in line with it being an arbitrary supposition. Thus numbers, far from being real are wholly subjective , and in fact completely formally defined.
There is no necessity for one and one to be two. It is that by definition alone.
Suppose I compare one object with another. How is it that I identify any object as one? It is by a process of physically separating out and placing the object protos or before all other objects. The placing down or kata of the object is that action that initiates the counting name "one".
As I repeat or iterate this process I must iterate the name in the Namespace. It is the sequence in the name space that has to be memorised to make sense of the whole of this iterative or recursive behaviour. The memorising of a cultural iteration is thus not arbitrary, but that to which it is subsequently applied is arbitrary beyond all arbitrariness!
This arbitrariness naturally means each form or object is unique, or can be named one. But each object by virtue of being unique differs in some way from every other.
Thus a unique object has to be given a unique name. We can replace "name" by " symbol or label or handle" . Later it will become clear that by substituting in this way we derive a symbolic model that can be applied in an arbitrary non sequenced way that has to be defined at every little nuanced change. This becomes the basis for symbolic ratioing, proportioning, reasoning , aggregation and factoring. It becomes a succinct way of identifying subjrctive processes of memory and recall , and allowing substantial focused manipulation of internal and external process actions.
In this way we address our existential interaction with our internal and external experience of the space within and the space without and all that populates them. These experiences I have called the set FS. It is a finite set, but it grows continually.
The set notFS is one that "ad infinitum" applies to, one we cannot finish counting ever, one which subsumed and consumes us all, whoever or whatever, in total annihilating exhaustion. But the hope is that recursion and iteration are fundamental to all things in that set, that is all things recycle in indescribably complex ways: that the possibilities are truly infinite!
|
|
|
|
« Last Edit: June 03, 2014, 02:57:14 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #12 on: June 03, 2014, 10:46:22 AM » |
|
As you know I do not accept that their is any process that I fo thst is totally objective nor for that matter is there anything I do that is totally subjective.
This interplay between inner and outer experiences I describe as a continuum. Thus there are no absolute poles but rather a Yin and Yang complementarity or conjugacy. In a bald sense a dynamic circularity or sphericity exists and I oscillate between the two in different frequencies for different states.
Thus when Monas was defined by the Pythagireans , the arbitrariness plas upon this cognitive dynamic deliberately. It is not meant to be confusing, but accepting of our real internal and external processes. Languages that have self reference or Tautology reflect this insight very well, even if modern thought has forgotten the role of self reflexive grammar or tautological grammatical construction. English, and English Grammarians thus put modern thinkers st a disadvantage.
Monas is any arbitrarily defined unit( Einheit), but as such it has no name. It has a purpose that gives it a name, Katametresee , from whence I fancy Metron is derived. Whether it is so or the other way round is not important here.,the measure or bowl or the act of doling out or placing down constitute an active process that defines reflexively a Metron and thus a Monas. A Monas is a standard unit, but it was not standard by consensus( which it now is) but standard by har-monia. This idea is a dynamic flowing of rhea into a singular (mono) form. These are parts that fit perfectly together to be a harmony a flowing together into one.
Thus the standard is what we call tessellation. A Monas must tessellate in multiple forms factorised by them..
These Monas/Metron multiple forms must be perceived by a process of factorisation to be defined as Arithmos! Thus Ruclids Algorithm in book seven is the beginning, the heart and the end of that entire book. Without it the concept of Arithmos cannot be understood.
But the book moves in a different orbit. It seeks to define and clarify not Arithmos, but Arithmoi!
Thus we find very many classifications of Arithmoi by their use, their origin and their purpose. The perception of multiple form arrived at by factorisation is the key message. Thus in every sense Division and aggregation are the 2 opposing fundamental starting points of all development of the Arithmoi.
To these Arithmoi we apply the cultural counting iteration. By this means we can sequence not just monads to form Arithmoi , but at every level we can sequence Arithmoi to form mega Arithmoi, say, and we can iterate again to sequence mega Arithmoi to form plassos mega Arithmoi, and by reiteration, plassos mega Arithmoi can be sequenced into bathos plassos mega Arithmoi and so on and so forth!
Arithmos are therefore the basis of recursion or iteration using the cultural counting iteration +1, or as Norman defines it, the successor function).
In this scheme it becomes clear that 1 as a name becomes useless. We have to say 1 whatever the form is..
However the cultural iteration itself is based on the fundamental spatial experience we call order. The words sequence and order define the same spatial experience and / or action or activity. We rec ignite this by defining different word called ordinal. The cultural iteration defines for us not only the name of an arrangement or a gathering, but also a sequence order. .
The two names ordinal and cardinal are fundamental activity distinguishes, but one is procedurally prior. We must order or sequence in order to name. Thus sequencing and ordering are fundamental processes in al we do , think or say or believe, or perceive.
The concept of protos or first therefore has a prime significance. I have described how by iteration we start with many firsts of different kinds of Arithmos. And these Arithmoi also have greater aggregations of which they may be protos or first.. Thus the Pythagoreans start with a Monas / Metron , that is they make that the first in order. Because it is first it's cardinal name can be 1.
However they can also start with any Arithmos and call that cardinally 1 . When that is done it becomes clear that there is a difference in these protoi Arithmoi. Not all of them are commensurable!. Simply put some protos Arithmos cannot be used as a factor of a larger Arithmos, because it is perisos, that is approximate in fitting that larger form!
The reason becomes clear, because even if the Arithmos and the protos Arithmos are set out in their monads they differ usually by a few monads. This few is always less than the protos Arithmos.
Book 7 deals extensively with ths system and hw it is to be used, but please do not be misled by the odd and even nomenclature or the use of multiplication instead of factorisation.
You will understand why prime is the Latin word used for these Arithmoi, because it is an ordinal notion meaning the first of any group of things.
In this case, Grassmanns concept of Einheiten models this analysis of the Protoi Arithmoi, and how they fill and encapsulate space.
The really interesting question is how foes the sphere fulfill this role, when it cannot tessellate? The answer, discussed by Apollonius reemphasises the iterative sequencing at different scales and why reality will ever exhaust and consume us!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #13 on: June 18, 2014, 08:04:50 AM » |
|
I have been busy of late and to a certain extent disenchanted.
As a young man I had fire in my belly, dragons to slay , causes to support and the world to put to rights. But now I see from the perspective of experience: youthful vigour is spent chasing paper tigers! The world like the earth rounds in huge cycles and what is curved cannot be straightened!
Nevertheless it is better to be wise than ignorant, because the wise one can find the right spot to effect a change that centuries of effort cannot. Kairos, the opportune time is always at hand , but a wise one is not.
It is instructive to read Hermann across his works. Youthful hope and idealism, replaced by hopeful endurance of rejection, and a willingness to learn from the school of knocks, to his emergence as an establishment figure mouthing those same words that at one time greeted his pubescent efforts! How what goes round comes round!
This is a rather technical paper which I will translate, slowly. The maturity of his thought in it reflects the times in which he lived. I am struck by how much that impacts on his terminology, his notational proclivities, his choice of symbols and phrases.
I remember reading how he successfully defended his primacy against St. Vainant, without ever realising the international scope of the bodies that he appealed to! Indeed the trans continental reach of these organisations was only jus being extended as electricity enabled telegraph communications to pass from the Americas to Europe and across Europe. This curious mixture of old practices and new thrusting modern conveniences was contingent on the intellectual societies of the day. Everywhere societies and guilds were springing up to pass on the new " wisdom" and practice in one form or another. Philosophical societiesn guilds of engineers and architects, Masonic and RosaeCrucian and other medieval "secret" societies or mystery schools all formed a network of " public" and private education from which some of the next generation of pioneers, inventors, and Scientists would come.
In short ignorance was no excuse, for any willing applicant as a supplicant to any of these societies , a willing postulant could be apprenticed to a master who would oversee and support the costs of their education, providing their benefactor saw grounds for doing so. Usually this was not philanthropy, although some were philanthropic. The real motivation was the gaining of some advantage, whether financial or social or both.
These " old ot" networks still exist even today and are an essential part of many social events one way or another.
Grassmann had access to the international journals of many philosophical societies, but he did not lays have time to read, keep upto date or contribute. Later in his life this changed and much of his later work is to be found in the collections of various journals and in several languages! However the main exposition of his ideas, what he wanted to promote most ardently are found in Ausdehnungslehre 1 and 2 as he refers to them.
Hamilton in his work set out new names for old long established ideas. This gave his presentations a new feel, but cut off centuries of established ' fact" forcing the reader to learn a whole new set of terms. This made old ideas seem to be newly discovered and gave cudos to the author(s), which might attract a benefactor to sponsor further " research" . Grassmann cuts through all this spin doctoring to provide the interested reader with " the Keys to modern Thought, especially mathmatical" . To paraphrase St. Vainant.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #14 on: June 20, 2014, 09:15:20 AM » |
|
I awoke this morning, my bed pointing along the north south magnetic Ley lines, due to a rearrangement of my sons room orchestrated by my wife, expecting some new insights and Natural Energy to spark interest. Considering again Grassmanns assertion of 3 equation groups as constraints on multiplication as a concept , using the monadic system denoted using the labels es and my current understanding of the commutative biproduct or bilineal product, the cyclical interchange product with product squares all interchangeably equated and finally all product squares summing to zero, I wanted to understand my interpretation of ordinary line segments and trig line segments.. Especially, since Grassmann derived his concept under the inspiration of the great trigonometrists of his time. It seemed that my translation of " zur Seite" might be misleading me from a simple Newtonian resolution of a line segment into orthogonal line segments! That is to say that projecting vertically or Senkrecht was the process of dropping perpendiculars onto a pair of line segments orthogonal to each other but joined through one point of the originating line segment. In physics this is called resolving a line segment into its orthogonal components! However we should perhaps more simply point out the application of Pythagoras theorem and trigonometric metrication. The reverse of this process of vertical projection onto orthogonal lines was called by Hooke and understood by Newton as, "compounding" the orthogonal line segments. Thus compounding was the process of finding the diagonal of a rectangular form. In this regard Grassmanns general product sum
AB + BC = AC
Represents a generalisation of that process of compounding!
However the process like the compound interest method on which it was based, at least methodologically, required the repeated iteration of the procedure of compounding line segments to achieve the desired orbit locus. Thus the compound line segment picked out the next position at which to repeat the procedure. This required drawing in the radial line and the tangent at that new point and finding the new compound line segment or diagonal. However Newton took the process into the next stage by also using rhombus or rhomboid forms to compound, especially when compounding for circular orbits. The concept of an outer product as a result of line segments stepping apart in a rotational manner and contrariwise an inner product as these same lines step closer together, relies on this vertically projected line segment I called a trig line segment. Grassmann makes some comments about it himself in which he clearly used the cosine and sine ratios And their relation to the Eulerian -Cotes radian arc measure. He also by analogy or rather logos analogos thinking connect this to the concept of the cosh and the sinh functions. I also note that the sum of these monads/ Metron units when squared coming to 0 is a related property to the Cotes DeMoivre theorems on roots of unity. I am reconsidering some concepts I developed of a prior or older spherical and circular geometry in which the fundamental symmetry of the circle/ spheres underpins the fundamental notion of Similar forms, the creation of parallel planes and lines , and the fundamental theorems of Thales from which Pythagoras theorem could be derived as an obvious consequence.of empirical pragmatic practice! Our notion of proof or demonstration skews our understanding of basic mechanical and constructional insights. What is empirically found to be the case, and thus inductively always expected to be the case is different from a formal system in which a statement is deductively demonstrated to be the case. The first is pragmatic and real, the second is ideal and formal. As a young mind it was hard to know what the words "real" and "formal" could mean, but now after much study it is clear that one is pragmatic and mechanical while the other draws on this, idealises it and removes it from any natural variation to a fixed static form. It is the Fractal , iterative Dyanmics of applying the formal to the real that enables us to apprehend that we are alive! Cogito,Sum! Returning again to the 1877 reprint of the 1844 Seminal Ausdehnungslehre I sense how Grassmann had come to the opinion that he had perfected the flaws of the 1844 version in the 1862 version. In particular he was confirmed in this opinion by the interest and application of his ideas by other prominent thinkers in his time. I have to be wary of jumping to tht conclusion just yet! Grassmann tried to keep the Ausdehnungslehre relevant and fresh to the developing mathematical and scientific Philosophy of his day. The New Geometries, that is projective and non Euclidean were shown by him to be best expressed by his concept of products. Others felt his ideas and methods provided a good ground for simplifying empirical research, and Schlegel,and Clebsch wrote extensive volumes on concepts that drew heavily on Grassmanns notation and style. The concept of groups and rings Grassmann saw as the New algebra and he wrote essays highlighting the relevance of the Ausdehnungslehre to this new thrusting war zone in mathematics. He developed ideas on the 3 dimensional space, and he analysed Hamiltons Quaternions in terms of the fundamental ideas of products in the Ausdehnungslehre. In everyway Grasmann promoted and advanced his concepts as keys to the modern philosophical developments, and their advancement. And still there were kernels of ideas in his works that required greater development! We can see much of this development in our mathematics and physics today, but what is also true is much of that has been erroneously developed!. This is not to say Grassmann is the pope infallible in the Ausdehnunglehre, as Klein invidiously implied, but rather that academicians ruthlessly baudlerised his wok and his ideas to promote themselves. Gibbs is a case in point. The section I am revisiting is..Vorrede p viii. I have retranslated it and really come to the same kinds of conclusions. At this stage Hermann is concerned only with the fundamental product notion: two adjacent " jostling" line segments form a parallelogram. Projection here is of both , one onto the other. The arithmetic product is solely the cosine , and the product is thus multiplied by a factor of cos 2ø the angle measure between them not being here specified but just identified. The later extension of projection comes from using the work of Laplace Lagrange etc as teeth cutting exercises in the development of his method. Ot is of interest to note that this continuous development and modification led to the " perfection" of 1862. However his Vorrede there is one of the mst pessimistic that he ever wrote, and betrays anxiety about whether he had made the right choices. He refers to the impetus of his brother as the Mathematician as if ready to blame him for any failure. Thus in 1872 when in fact he received favourable responses he shows a remarkable assured ness of the unassalability of his work. I also note a nationalist pride being portrayed in his comments on the work of Hamilton. It is not that he dismisses Hamilton, but rather he appeals to the Prussian pride in their own works and productions. Why he asks promote an international author when homegrown authors not only tackle the subject but tackle it better! Klein relates how in this tumultuous time of wars and revolution , when the whole geopolitical scene was delicately balance that rioters were seen in the streets shouting Grassmanns name against those shouting Hamiltons! It was perhaps diplomacy that made him and academia marginalise these excesses. Indeed most learning was from the French Ecole , but most hated Napoleonic France vehemently. This was not a good time to agitate against a French imperial power! |
|
|
|
« Last Edit: June 26, 2014, 11:25:48 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










