|
jehovajah
|
 |
« Reply #345 on: April 07, 2015, 04:34:07 AM » |
|
The cyclus group has winkled out another flaw in my understanding. The design of the Middler product was completed by adjusting the result of an Assocative product., the everyway unioning of 3 line segment factors. The goal was to make such a factor arrangement the result of a subjugating knitting applied on the right (RHS) abc =a(bc). This is a limited associativity, and we cannot assume the Middler product is established for subjugation from the left(LHS) abc=(ab)cBecause of this, the cyclus group controls the "rotation" of the outwardly completing process! The design or artifice in this construction occurs under the noses of Mathematicians hungry for a multiplication process but not aware that they are ignorant of the referrent of that word. Hermann has been redefining words and reassigning meanings from the outset. The induction is the in-depth core of that mind learning process. So now under the guise of mathematical language he can design a mental process that models rotation. The outward completing entity is simply a tour around the line segmnts. This is why the cyclus group is restricted as a permutation group, and split or co factored as a permutation group into a clockwise rotation and an anti clockwise rotation. On the clock face 1,2,3 is clockwise , 1,3,2 is anticlockwise. The Ergänzung process is an assigning process. It assigns a pair to a third completing entity. It does so by utilising the status sequences of the cyclus group. 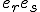 is assigned to 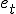 strictly in the cyclus status order. When we step back from this mind conducting process we see that we have " mapped" 2 to 1 . This mapping is comparable with a factor mapping common in multiplication tables or number bonds. Because of this similarity we are conducted to utilise this relationship as a product. However the result of this "product" is to be interpreted as a (RHS) subjugation by the intervening line segment rotating one line segment into the position of the Third. Consequently, as I pointed out, the spreading out product is transformed into this outward completing format. Whatever the spreading out product was assigned to in any other use , here in the Middler product it is assigned to this rotating of line segments role concording with the cyclus group constraints. When you design construct and programme a processor, you know you are prescribing exactly how it works. Yet you probably still think you are copying some objective truth " out there". There is no doubt Hermann and Hegel held this opinion. But unlike their contemporaries they felt this Geist or mind was embedded in everything, and they were merely giving the clearest expression of it. We can take it another way without harming that sentiment: we pragmatically have to set out ways to " mimic" observed, expected or desired or inspired visions of behaviours. Whatever you care to believe the truth is we have to find ways of implementing behaviours, and that from the outset is Hermanns Goal. Justus hoped that this unblinking rigorous manufacturing of behaviours with the caveat of the Simpest or most Natural expression of doing so was expressing elemental truths of the Geist, beyond question or artifice! I question that assumption, but hasten to add that many fine and impressive structures of the mind have been built on this sentiment. Yet questioning it may very well develop new and better expertises. Indeed, but first I would understand the full range of their conception , these Grassmanns. |
|
|
|
« Last Edit: May 15, 2015, 12:09:54 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #346 on: April 07, 2015, 10:16:37 PM » |
|
Commentary on page 378 The main goal here is to show how the Middler product works. By using the associative rule Hermann shows that the set up works as a " imaginary" magnitude. Thus zany 2 line segments product as constrained by the Middler product. In addition, the elemental line segment appear to product on the right like i the imaginary magnitude, and also like i,j,k. If the line segments are parallel, only the colliding in product is used to give the numeral 1, the 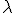 makes it -1. Thus 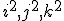 take this value. If the line segments are perpendicular only the outwardly completing " product" is used. Thus the quaternion products are reproduced. The Middler product takes line segments and makes them behave like imaginary magnitudes! So what are we witnessing here? The demystification of the imaginary magnitudes? Not really. But we are seeing that imaginary magnitudes are not necessarily special " divine" entities. They can be constructed from familiar entities and behaviours. The real demystification of imaginary magnitudes is the work Hermann did on the swinging line segment. The other point to be addresses is the product design pricess itself. Iday we have virtually fixed designs for the colliding in nd spreading out products, but here Hermann makes clear they are labels for different knitting processes and have to be designed to suit. Each realised design, thn is just one instance of many other possibilities that fulfill the criteria. This is important as we go o higher stages: the design has to be consistent with the constraints at that step level. The products at each step level will therefore necessarily be different to those that come before, but should retain some design link through the design constraints. Finally if like me you wondered what on earth a vector multiplication could be or how it could make sense, I hope you realise that the concept of multiplication was the problem: it has never been understood as an imposed design for some imaginary entities called " numbers", and never allowed to reveal itself as such, controlling our thinking despotically, and for the purposes that others may dictate rather than the solution of the problem we may be seeking to resolve, |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #347 on: April 22, 2015, 02:04:02 AM » |
|
As I work through page 379 I appreciate the simple genius of Hermanns style.
I cannot say I have ever apprehended quarter ions as geometrically intuitively as this, nor with such facility for extension and application,
The role of theodorus spiral is crucial for the extension Into higher dimensions or stages beyond n=3
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #348 on: April 25, 2015, 10:44:58 AM » |
|
The Place of Hamiltons Quaternions in the Doctrine of Extending/ Extensive Magnitude By H. Grassmann. In Stettin -------------------------------- Page 379  is a quaternion, thus 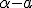 one besigns knowingly as the quaternion conjugate to that one, From more fundamental assigning the rule is : "if
( )( )(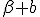 ) = ) = 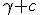 exists, exists,
thusly exists also
(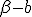 )( )(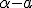 ) = ) = 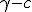 " "
In practice the colliding in part of the first product is ![\alpha\beta-[a|b]](/cgi-bin/mimetex.cgi?\alpha\beta-[a|b]) therefore this 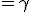 But ![\alpha\beta-[a|b]](/cgi-bin/mimetex.cgi?\alpha\beta-[a|b]) is also the closing in part of the second product . Far off against, the spreading out part of the first product is ![\alpha b+\beta a+|[ab]=c](/cgi-bin/mimetex.cgi?\alpha b+\beta a+|[ab]=c) the spreading out part of the second is ![-\alpha b-\beta a+|[ba]](/cgi-bin/mimetex.cgi?-\alpha b-\beta a+|[ba]) , that brands , there ![[ba]=-[ab]](/cgi-bin/mimetex.cgi?[ba]=-[ab]) exists, Like  Therefore the second product 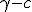 It is immediately clear that this lets itself extend onto whimsically many factors, Therefore (11) Whimsically, The Product of many Quaternions is conjugated to the "turned-around ordered" product of the conjugated quaternions
It represents , this proposition, the formula (14) by considering Dillner, out of which formula his formula (13) goes henceforward, If the colliding in parts ( 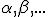 ) one sets null. If the line segment  exists thusly becomes [ 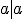 ], what I the short way have besigned  , like 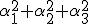 and represents the Quadrature (Quadrance) of the Length of that line segment. According to this Analogy I name , if  exists ) That brands, =\sqrt(\alpha^2 - a^2)) the length of the Quaternion 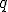 ( concording to Hamilton the Tensor) Now one Multiplies the first formula in (11) by the second, so one holds out (  )( 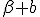 )( 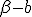 )( 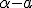 ) = ( 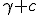 )( 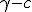 ) That brands (  )( 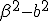 )( 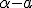 )=  There 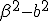 = 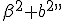 is a tally mark, thusly its positioning is like valued, therefore we can the factors 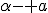 and 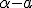 back up together and hold out ( 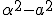 )( 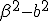 )=  Or (111). ) ) = ) . There, that brands, (this lets itself extend onto many Factors ) (111). the Length of a product of quaternions is the product out of the Length of the factors It arrives next, therefore only upon a multiplication of the quaternion monads, that brands, the quaternions to which length 1 exists. Now Let 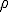 be the length of a quaternion 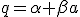 , where  is a line segment of the length 1 Thusly 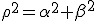 . Now let 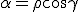 Thusly 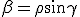 exists Therefore  ) |
|
|
|
« Last Edit: May 14, 2015, 10:14:48 AM by jehovajah, Reason: Subtle mark spotted that changes the notation! »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #349 on: April 25, 2015, 12:31:21 PM » |
|
Commentary on page 379 The underlying processes described, Hermann is now able to use the rules laid down and decried exquisitly simply. The Ansatz or keynoted rules rhetorically explained after a symbolic presentation, are careful not to express subjugate product rules. The issue about the length or tensor of a quaternion is argued analogically. . However, the colliding in product is clearly identified as the length of the Quaternion. Because this is not a length inncartesianmcoordinates, Hamilton named it the Tensor, again meaning stretch or Ausdehnung, but Hermann argues it is a length, and indeed it is a length found in Theodorus spiral. . The choice of shorthand notation for the length of a quaternion highlights the issue of labels. The root label is not an operator, butbanlabel drawing attention to a complex process. Thus the ) is not an operational label but a marker drawing attention to a complex process. This is precisely why producting ) does not follow the arithmetical rules. The sign draws attention to new rules that have to be applied. In this context the colliding in product of both the quaternion with itself and its conjugate with itself have the same out put value, and this is what the likening of the labels for the length of the factors draws attention to. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #350 on: April 25, 2015, 05:02:57 PM » |
|
Commentary on page 379 I make thousands of typos. Some can be disastrous to the sense of a passage. Hermann has made typos and thee he addresses in errata appendices or corrective essays. Unfortunately this article was one of his latest just before he died and so I do not think he had much time to deal with errata. I found one erratum in expounding on the colliding product output results which wasa misplaced Ergänzung sign. However the issue I am looking at is the definition of Quadrarure or Quadrance. It is not hard to see the preeminence of Quadrature over Iengthj, and it is this that caught my attention. The quadrance is a modern term, coined by Norman Wiidberger, for quadrature. Hermann defines it as the colliding in product for a line segment multiplied by itself. Similarly he defines the quadrance for a quaternion 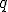 as the product with its conjugate 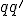 . This is not clearly stated literally and so an important identity is conflated, probably by a typo . 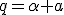 Thusly ![q^2=(\alpha+a)^2=\alpha^2+a^2+2\alpha a=\alpha^2-[a|a] + 2\alpha a](/cgi-bin/mimetex.cgi?q^2=(\alpha+a)^2=\alpha^2+a^2+2\alpha a=\alpha^2-[a|a] + 2\alpha a) Now 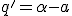 the conjugate Thusly ![q'^2=(\alpha-a)^2=\alpha^2+a^2 -2\alpha a=\alpha^2-[a|a] -2\alpha a](/cgi-bin/mimetex.cgi?q'^2=(\alpha-a)^2=\alpha^2+a^2 -2\alpha a=\alpha^2-[a|a] -2\alpha a) Thus we can see that the Quadrances are indeed both like, as the colliding in part of a squared quaternion. Using the conjugate removes the spreading out part leaving just the quadrance. The typo i think is in the Dillner reference where the length is given by two square roots That are not clear. The first is but the second appears as wishful thinking or a typo. I have since come to understand better Hermanns presentation. By defining the quadrance of a line segment product as ![[a|a]](/cgi-bin/mimetex.cgi?[a|a]) , or rather the quadrature and then using 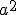 to represent that he subtly uses synaesthesia of labels to connect this instance to the general Middler product. Thus we have 2 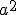 's here, the first is the set up for the Middler product, the second is the output result. Because the output result switches sign the queer looking quadrance likening is in fact accurate. What Dillner was stating I do not as yet understand. |
|
|
|
« Last Edit: April 25, 2015, 08:41:48 PM by jehovajah, Reason: Misunderstanding Hermanns argument. »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #351 on: April 25, 2015, 09:16:17 PM » |
|
I have read and retread this page (379) and find the clever use of labels unsettling. One gets the feeling that black is being turned into white before your eyes!
The use of the same symbol in different contexts to mean nearly the same thing is tautology. It is also recursion. It flips the meaning of a symbol between 2 states both of which are decideable by the other! So the conjugate product is different to the quaternion product but both relying on and have their meaning in one another!. You cannot have one without the other!
The use of symbol as Ansatz or set up explanation andvthenmas output result with only a sign change indicating the change between the 2 states requires some careful and intense observation.bbut it is similar in ilk to Hermanns assertion that 2 dynamics are occurring at the same time in the seemingly docile line segment!
I read it again and noted that I had put :
"That brands".
Thus it would seem Hermann was branding the quadrature analogy . Branding is a way of defining to what a thing belongs. Thus his little spiel about an analogy deals with the analogy, and the likening deals with a necessary term change to confirm it to the Middler product.
I think I would have used a different label say A, to signify the output from the Middler product, but the general rule is not specific
14/5/15 just spotted a subtle mark that corrects the issue, effectively using A as I said. Hermanns subtle markings I have edited into the translation
|
|
|
|
« Last Edit: May 14, 2015, 10:21:26 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #352 on: April 27, 2015, 10:17:38 AM » |
|
Normals pizza topping is relevant here.
<a href="http://www.youtube.com/v/LFpWk5G8DOY&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/LFpWk5G8DOY&rel=1&fs=1&hd=1</a>
<a href="http://www.youtube.com/v/LFpWk5G8DOY&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/LFpWk5G8DOY&rel=1&fs=1&hd=1</a>
Norman is well constrained and trained in his Grassmann style, but by placing Numbers at the foundation of his development he ensures commutativity or rather gleichgültig vereinigung of any elementary factors is embedded in his basis.
However commutativity, by now I realise is a welcome casualty of the greater Freedom Hermann gives to our thought patterns, because if we do not include it in the basis we do not expect it to be fundamental constraint.
What Norman is calling a metric structure Hermann has been generally calling the product design.
In addition, while I am sympathetic to. Normans rant ob infinite processes etc I do not apply it to Newtonian and Pre cantor set theoretical presentations of the trig ratios, or series expansions.
Ad infinitum has one meaning: toward no finite assignment . This is and was governed by the principle of exhaustion. This principle naturally allows a truncation of an ad finitum process through exhaustion. Thus the old school geometers were thoroughly Archimedian: they did not countenance infinite processes as sensible!
Therefore the trig expansions are not necessarily to be taken as infinite processes, at least we do not have to accept this version of it . In adoptingbthisbpoint of view we necessarily reject the infinite Real number line concepts and adopt the ad infinitum rational measuring lie concept . Which is precisely Normans point.
Hermanns point is already well made: his style, using line segments as continuous extending magnitudes, and concommitantly as symbols of Intensive point- like magnitudes provides a simple consistency in our thought patterns that is extremely fundamentally useful! You ca see Hermann gets to all of this very directly and understandably by his general set up, and that is for quaternions!, not jus complex numbers!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
|
|
jehovajah
|
 |
« Reply #354 on: May 15, 2015, 12:07:43 PM » |
|
The Place of Hamiltons Quaternions in the Doctrine of Extending/ Extensive Magnitude By H. Grassmann. In Stettin -------------------------------- Page 380 It brands  the Mass/Measure and 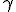 the corner angle of the quaternion, while  concording to the above entity is the Quatern monad quality. The product like measured Quatern monad qualities conducts to very simply performed results . In the performance let it be  the Mass of 2 Quatern monad qualities and  and  their corner angles, thusly one finds ( 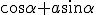 )(  )= +\cos\alpha\cos\beta-\sin\alpha\sin\beta) There 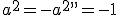 exists Therefore = + a\sin(\alpha+\beta)) That brands, " like measured Quatern monad qualities one multiplies, in which entity one adds their corner angles" Herein lies shut within That one a Quatern monad quality with a completely positive Tallymark exponentiates, in which entity one multiplies its "corner angle" with this Tallymark . Also for the exponentiating with a fractional and negative Tallymark we can the same concording idea firmly hold, but with the restricting That the corner angle which associates to exponentialed quaternion remains in inner part of the boundaries of a completed unrolling, to the considering game, Between 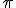 and – 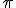 lies (everyway liken to my Arithmetic Stettin 1860 Nr.426–433 A definition for these knittings is necessary, and plainly thus the above given to you restricting, because one one sonst to go the logical ruling everyway pushed' That one the same matter allows not upon two differing artforms to define, specifically if both the definitions themselves contradict. But last thing would become to be by considering the exponentialing with fractional exponents of the case , if one that restricting lets not to step in. Thusly to the considering game, exists + a\sin(0)) = + a\sin(2\pi)) Both might be exponentialled with 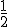 , if one firmly set, the Quatern monad quality with 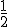 to , naming(hiesse) ito multiply ts corner angle with 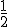 , differing entities to deliver Because first bracket would become thereconcording 1 to deliver. But last bracket + a\sin(\pi)) that brands –1 Above definition firmly set, one outwardly holds If  between 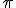 and – 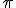 lies and 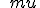 real is + a\sin(\alpha)^\mu) = + a\sin(\alpha\mu)) That brands " A Quatern monad quality, the corner angle of which between 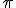 and – and –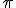 lies, one exponentiates with a real Tallymark, in which entity one its corner angle with this Tallymark multiplies. lies, one exponentiates with a real Tallymark, in which entity one its corner angle with this Tallymark multiplies. Here is the Dillner presentation ( Nr.30) unsatisfying. Plainly thus I everyway miss by considering the Division (Nr.12) the demonstration of the one-assigned quality of the Quotients. This may be here outwardly completed. If 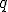 is a quaternion differing from Null, thusly empowers as Definition from 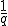 the likening 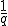 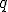 = 1 If now  is a whimsical line segment from the lengths 1, thusly 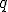 lets itself present in the thought pattern 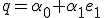 Now let be 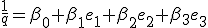 , where 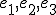 build a representation of a Normal unioning Then one outwardly holds to the concording from  the likening |
|
|
|
« Last Edit: May 15, 2015, 12:54:43 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #355 on: May 15, 2015, 01:16:16 PM » |
|
Commentary on page 380
It is quite clear, in fact extremely so, how easy this method makes the teaching and understanding of quaternions. In addition it provides a ready geometrical interpretation : the sphere enclosing all right cones about a given line segment with beginning element at an arbitrarily chosen origin.
Not even Norman has exposited quaternions so naturally. Certainly Dillner is taken to task!
The cones themselves are surfaces around the line segment that form a Winkel in this case a solid corner angle or apex to the cone. Evenso it is not a specified by a line segment but by a calculation based on dropping a perpendicular of the required quantum( bounded magnitude) to Give the numerical value for the sine of the ( half) corner angle of the apex.
This is the construction based on the notion of a quaternions length.
The Cotes DeMoivre theorem is used to explain Exponentiation, and without an exponential function in sight he derives all the exponential function result: but note not just for the so called complex valued functions, but for the quaternion valued ones!
Study this page carefully! I do have some small corrections to make, but it is a real gem!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #356 on: May 15, 2015, 02:34:09 PM » |
|
The translation of Justus Verbindungslehre in the V9 thread is so crucial to understanding Hermanns work that I urge the reader to read that thread alongside any other thread re the Ausdehnungslehre.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #357 on: May 16, 2015, 07:29:56 AM » |
|
Just a note to warn the reader: do not allow yourself to be fooled anymore by imaginary or complex numbers or complex variables.
Hermann has demonstrated how we construct these concepts from quite understandable processes and construction behaviours. In addition he has firmly dispelled the gauche" oh it acts like a rotation" response because it was constructed from a cyclical interchange deliberately and carefully.
Of more interest here is the use of the " reel" tally mark.
It is to be noticed that he uses a german expression not a Latin one, indicating it is a German derived notion. Indeed it was a notion contemporarily derived by Dedekind. Norman critiques these ideas and the Modern useage of them, but here Hermann uses it deliberately in a geometrical construction, and thus in a geometrical sense.
The insistence on reel numbers being notationlly narc curate is clearly a joke. We use letters because we know we cannot conceive of these quantities by integer or rational means, apart from ratios of "prime" quantities. So we are left with the geometrical constructions of these quantities and the general geometrical manipulation of them, or indeed rational,approximations.
Reel numbers conveniently allows Hermann to describe one rule for all concrete cases , no matter how accurate we need to be.
In particularvSir William Rowan Hamilton, derives the real numbers in his progression towards the complex labelling of notion of imaginary values! His derivation of the real Cardinal numbers is firmly based in a geometrical analogy of Time in continuous progression. These reel representations are always letter variables because we cannot pin the concept down to a unique ratio of whole units . So they are not real numerals, but labelled variables and this is how Hamilton and Herman understood the adjective real/ reel.
There are no real numbers as such just continuously extending variables.
The use of these continuous variables is heavily proscribed, and they do not deserve to be called numerals!
We may conceive of then as variables that are geometrical in nature and which may take on any specified geometrical magnitude that has been cut off . Sometimes that magnitude cannot be written as combinations of geometrical Metrons. in this case it represents a truly transcendental quantity. '
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #358 on: April 02, 2017, 11:25:02 AM » |
|
It is now 2 years since I posted in this thread. But the personal problems which have kept me at bay have not dampened my interest in the Grassmanns or in the effort to meditative lay tranlate some ( if not all) of Hermanns work.
It occurs to me , after some time that the reverence for mathematics I inculcated has been a mixed blessing. I have had to see the material with clean eyes, and I thank, in articular NJWildberger for taking the scale from my eyes while maintaining that enthusiasm for what really matters in this expertise of thought patterns in identifying, defining analogous processes of aggregating counts and designing complex processes of counting. , of which the multiplication processes are the most complex.
But I thank the pythagoreans for setting out an introductory course in philosophy of measuring by counting metrons, and how these methods may be applied to constructing forms sketched out by hand in the ground or thought in the minds eye, and how these metrons may be compared in a study or logos of their relationships during dynamic developments.
It is this philosophical set of principles and expertise of measurement and counting that lead to the pythagoreans study of both static and dynamic phenomena in our experience of this cosmos.
And the Grassmanns were able to bring out to the primary school level methods and processes that gave students essential and key insights into this expertise.
I say primary level because they were primary level teachers although Hermann aspired to be at he top of his academic profession .
The Ausdehnungslehre 1844 was therefore written for aspiring primary school teachers to prepare Prussian children for the new revolutionary nd industrial era that was upon them. It was essential or Prussia established itself as. Power to be reckoned with, and this Bimarck and others throughout this great land were determined to do as urgently as possible.
The eclectic nature of the Susdehnungslehre 1844 was so inspiring that day, despite it's lack of recognition at the time it is now the fundamental basis of all higher learning in the sciences.
Why I was inspired to write was because one of the fundamental products that Hermann identified was the um of squares summing to a suare. . The other product used extensively by him was the closing together product, which became the dot product for vectors or rather line segments. Both these products come from the use of the right triangle as a fundamental planar Metron , applied in orthogonal planes in space for 3 dimensions, but in n intersecting planes in pace for n- dimensions
The interchange of 2 line segments entirely within a plane, that is the interchange is constrained to the plane, requires rotation in the plane, and it is this constraint that introduces the switching of signs along with the interchange.but who would be rigorous or anal enough o insist on that? The Grassmanns, and particularly Hermann. These constraints made a symbolic arithmetic of lines( Arithmoi) precise and less ambiguous. .
From these definite constraints both Normn J Wildberger and Hermann Grassmann , Hestense and others have shown a rich powerful clculative method can be developed
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #359 on: April 25, 2017, 03:50:10 PM » |
|
Der Ort der Hamilton schen Quaternionen in der Ausdehnungslehre Von H. GRAssMANN in Stettin, Da die Ausdehnungslehre nur die eine willkührliche Annahme macht, dass es nämlich Grössen gebe, die sich aus mehr als einer Einheit numerisch ableiten lassen, und sie von da aus in ganz objectiver Weise fortschreitet, so müssen alle Ausdrücke, die aus einer Anzahl unabhängiger Einheiten numerisch ableitbar sind, und also auch die Hamilton's chen Quaternionen, in der Ausdehnungslehre ihren bestimm ten Ort haben und erst in ihr ihre wissenschaftliche Grundlage finden. Dies ist bisher nicht erkannt und Göran Dill ner in seiner lehr reichen Abhandlung über die Quaternionen (Annalen XI, 168 ff.) thut der Ausdehnungslehre nicht einmal Erwähnung, obgleich er eine ganze Reihe von Sätzen aus der Theorie der Quaternionen ableitet, welche schon in meiner Ausdehnungslehre von 1844 (&1), und ebenso in der späteren Bearbeitung von 1862 (&2) ihre viel einfachere und aus der Natur der Sache entspringende Begründung gefunden haben. Auch ist es verwerflich und der Lehre von den Quaternionen wenig förderlich gewesen, dass man nach Hamilton's Vorgang einfache und längst bekannte Begriffe mit neuen, oft recht unpassenden Namen bezeichnet hat, wie "Vector" statt "Strecke" Tensor statt "Länge " oder "numerischer Werth (&2 414), u. s. w.
Die Hamilton's chen Quaternionen entspringen aus einer der Multi- plicationen, welche ich (in meiner Abhandlung "Sur les diflérents genres de multiplication ", in Crelle's Journal Bd. 49 S. 130 ff.) dargestellt und an die 3 Gleichungsgruppen (1) eres
=eser,
(2) eres + eser
=0, e1^2=...en^2
(3) e1^2+...+en^2=0
geknüpft habe, wo e1, e2,... en die von einander unabhängigen Ein- heiten und er und es, zwei beliebige von einander verschiedene dieser Einheiten bezeichnen, und zwar knüpfen sich die Quaternionen für den Fall, dass n =3 ist, an die Multiplication, deren Bedingungsgleichungen
The place of the Hamiltonian quaternions in the theory of extension of H. GRASSMANN in Stettin, since the theory of extension makes only one assumption, namely, that there are magnitudes which can be derived numerically from more than one unit, and from there on in whole Objectively, all the expressions which can be derived numerically from a number of independent units, and thus also the Hamiltonian quaternions, must have their definite place in the theory of expansion and only find their scientific basis in it. This is not yet known, and Göran Dillner in his instructive treatise on the Quaternions (Annals XI, 168 ff.) Does not even mention the theory of the expansion, although he deduces a whole series of propositions from the theory of quaternions, (& 1), and also in the later edition of 1862 (& 2), have found their much simpler reason, which springs from the nature of the matter. It is also objectionable and of little help to the doctrine of the quaternions that, according to Hamilton's method, simple and long-known terms have been designated with new, often quite unsuitable names, such as "vector" instead of "distance" Werth (& 2 414), etc
The Hamilton quaternions arise from one of the multiplications which I have presented (in my essay "Sur les diflérents genres de multiplication", in Crelle's Journal, Vol. 49, p. 130 ff.), And to the three equations (1)
= Eser,
(2) eres + eser
= 0, e1 ^ 2 = ... en ^ 2
(3) e1 ^ 2 + ... + en ^ 2 = 0
Where e1, e2, ... en denote the independent units, and he and it, two arbitrarily different ones of these units, and the quaternions in the case where n = 3 The multiplication, its conditional equations
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










