|
jehovajah
|
 |
« Reply #30 on: July 12, 2014, 11:30:40 AM » |
|
Interestingly, the addendums to the 1844 version contain additional insights Hermann had just before he died. But of interest to me is addendum III , because he summarises all the main results there and gives some exercises with answers!
There is also a guide to where the artwork or figures he added in the pullout at the back should be directed!.
Originally I started on the 1862 version, but was frustrated by Hermanns constant reference back to the 1844 version. The new imprint (1877) of the 1844 version is indeed a good collection to research from.however if you just want to get the gist and use the formulae the 1862 version would be a better start.
For me, the research has proved invaluable in pointing out several errors introduced by later developers, or if you like several modifications they have made. I use the word error advisedly particularly about Gibbs version. Gibbs admitted that he really did not have a clue what Hermann was talking about in terms of his MULTI algebras. Thus the Gibbs version that underpins modern vector analysis may contain significant flaws.
The geometrical Algebra and Geometrical Cakculus approach is more consistent with the Grassmann tradition, but I would not claim that it ihas been clearly presented or taught until very recently. I am more confident now that Hermanns ideas can be quickly distinguished from those which have been added or modified by other later developers
As Hermann himself poited out, this is a work in progress , and refinements and modifications are to be expected, but it is comforting to know that we are not having the wool pulled over our eyes by Mathmagicins, and this is a genuine system that reworks everything!
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #31 on: July 15, 2014, 06:24:16 AM » |
|
So I have given a lot of thought th what " die Beziehung zur Addition " might refer to and why it is the multiplikative Beziehung that has to apply.
Today mathematicians talk about the rules or. axioms of a group and thy specify the " operation" that essentially defines the group in terms of how combinations or associations are defined. If a group has 2 operations defined on it then it is on the way to being classed as a ring.
The interaction of those 2 operations is their Beziehung or relationship. When I was being taught arithmetic with natural numbers I was taught an " operator" precedence or a convention of operation order .BODMAS. This Mnemonic describes the relationship between all the operations in a complex calculation. In this scheme Multiplication is done before Addition , and that before Subtraction, unless a Bracket intervenes.
This is the multiplicative relationship .
How it relates to addition requires us to bracket addition, which essentially instructs us to reverse the operator precedence. In another sense it means that the final act is multiplicative. However we also perform an operation called expanding the bracket. This is called distribution of multiplication over addition.. What that means is we multiply the parts being added first and thn add the products.
This whole set of conventions is what I think this phrase is referring to .
Grassmann has a specific model
AB + BC = AC .
This is a sum but he came to regard it as a sum of products. In this case it is a product of points.
(A +C)B = AC
This simple observation reveals an analogous form at all levels . Thus for line segment a,b,c,d where
ac is a product and c =b+d
So ac= ab + ad
This law is crucial to constructing any algebraic ring , and for evaluating line segment products, and essentially it allows transformations to be equated under strict constraints.
There is another distributiyity rule and that is multiplication over multiplication. Strictly speaking it is multiplication over associativity. Buried within this rule is a property called commutativity. Because of its algebraic derivation commutativity does not reflect Grassmanns geometrically derived vertauschen und umkehren concepts, which are purely cyclical. This is a point I cannot emphasise enough.
Hamilton and Boole are often cited as chief instruments in the liberation of Algebra from Arithmetic. However Grassmann took the opposing direction. He sought to establish the derivation of arithmetic from general and sound geometrical principles and relationships. Thus he starts with ordering in space , and from this ordering he can develop sequencing rules that are countable. Within that framework he can develop sequences of points, line segments, plane segments etc. then the inter relationships between these elements in each sequenc can be linked to " higher" ordered sequences. Thus a sequence of 3 points can be linked to a triangle form in a plane or, more importantly a circle form in a plane. A sequence of 4 points can be linked similarly to a spherical or rectilineal form in 3d space, and so on.
From these relationships and constraints the principles of the geometries of these forms can then be derived.
In this way Hermann constructs a mathematic that fully accords with our conscious interaction with space, and so becomes an apt model by which we might describe spatial forms analogously.
|
|
|
|
« Last Edit: July 16, 2014, 09:59:04 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #32 on: July 16, 2014, 10:22:11 AM » |
|
There are some interesting consequences of the point product concept, but these refer to the Barycentric Calculus. Because Möbius did not include a point product in his calculus he was overtaken by Hermanns ideas in the Lineal Algebra.
AB + BC = ( A + C)B= 2PB = AC
For this to work the triangle midpoint theorem has to be applied to determine P. PB then becomes a line segment parallel and in the direction of AC . The scalar 2 which weights the point P is applied to PB only if coincident points are acknowledged. This means that there are 2 collineal line segments ending on B. if both were summed by projecting one by the other we would get a line segment parallel to AC with the length of AC .
Returning to the single line segment case A+C=2P means the two points sum to a point which is 2 coincident points P. this point is a heavy point! We cannot locate it unles we can show AC = 2AP
Essentially this is what Grassmann defines in his point Algebra. We can locate it by bisecting the product AC and that can be done by using a pair of compasses
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #33 on: July 22, 2014, 01:08:50 PM » |
|
I thought it best to keep this reference handy to this thread. http://books.google.co.uk/books?id=lSoJ2tJKfIEC&pg=PA250&lpg=PA250&dq=the+moment+of+a+rectangle+newton&source=bl&ots=PxkxmARNIi&sig=OfWOgOTdKZlDsV6NP7LusAehiJ0&hl=en&sa=X&ei=FInMU8qGBun07AbX4oHYDQ&ved=0CCgQ6AEwBA#v=onepage&q=the%20moment%20of%20a%20rectangle%20newton&f=falseThe concept of a product being the sum of products has far reaching applications, but the essential geometry of it as rectangles and parallelograms I doubt if but a few know. Certainly Newton and latterly Grassman grasped it . The uses to which the put geometrical invariants , identities etc are perhaps best described in the Work of. Norman Eildberger as he researches these geometrical thinkers in depth. For my purposes here it is the rectangular product which is relevant. The argument I have set that in fact this is the " inhere" product has many ramifications, not the least being that the inner product is the metric evaluation principle for the general outer produc ( sic, if the outer product is ab then this is evaluated by the inner product ABsinø, or indeed any other formulation that gives the area of a rectangle pertinent to the parallelogram form) The use of the rectangle by Newton shows liberality of thought in modelling terms. The proposition in book 2 ( proposition  on which his argument or case is based needs first rejigging for the general rectangle, which is not too difficult to derive. Having done this the diagram must needs be seen as momentarily static in a flux inorder to derive Newtons flux moment for a rectangle. The relevance here is that it now becomes an inner product in Grassmanns scheme whereby he may evaluate the flux moment of a general parallelogram. In any case the method as defined by Newton carries over exactly into his handling of polynomial expressions. Indeed he requires that any such expression of dynamic quantities be in that form. You will notice that Normans treatment of differential calculus , ascribed to LaGrange follows this method precisely. This should be of little surprise as LaGrange was the chief promoter of Newtonian ideas in France and Europe. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #34 on: July 27, 2014, 11:15:27 AM » |
|
I find myself still wondering about the inner product, but I have now determined that this is due to a subconscious interaction with the English concept( geometrical) " inner". Grassmanns explanation for the worde " innere" is Annäherung. Thus this product should be expressed as the Closing in product and the exterior product as the Spreading out product.
The Spreading out product is defined in terms of the bounding line segments for the parallelogram form. The Closing in product is defined in terms of the dropped perpendicular from one of the bounding line segments onto the other AND that other. The constraints or rules of cyclic interchange differ because the closing in product is designed to evaluate the Soreading out product.
It is clear that sometimes the perpendicular will fall beyond the line segment. However this is catered for by Extending the line segment( ie using a multiple of the line segment)
If the bounding line segments cyclically interchange then the sign of the product " switches" also. This means that the Closing in product also has a sign change, but interchanging the perpendicular and the appropriate line segment cyclically is not allowed to change the sign. That is it is a design constraint on the system of synthesis and evaluation that the closing in product does not change the sign on cyclic interchange.
The parallelogram presents 2 "rules" in one form. Summation of line segments is defined by AB + BC = AC
And product of line segments is defined by AB.AD= ABCD on cyclic interchange AD becomes –æAB because it now points in the negative direction to the positive direction established in AB initially. This is the principal orientation and the principal direction in that orientation was set by AB similarly AB becomes šBC because the principal direction was set in BC// to AD in that relative orientation. Instead Grassmann writes AD.AB = –AB .AD to denote these rules.
|
|
|
|
« Last Edit: July 27, 2014, 09:17:14 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #35 on: July 27, 2014, 09:37:22 PM » |
|
The evaluation of the Spreading out product fails when the bounding line segments are parallel. In that case that product should be a null parallelogram. However in that case a line can be constructed by projections However the Closing in product is arithmetically 0, so one can say the Spreading out product takes the value of the closing in product.
At the rectangle form the spreading out product is evaluated by the line segments. The Closing in product is not defined as no line segment can drop a line segment vertically onto the other, at least it is indistinguishable from the bounding line segments. Here the Closing product should also be null, but it can take the value of the spreading out product.
There are other products created by this perpendicular projection. The Shadow product for example is 0 at the same moment as the Cloing in product becomes null or void. In fact the Shaddow product is often confused with the closing in product, of which it is a part
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #36 on: July 28, 2014, 10:46:24 AM » |
|
I'll toss in some rambling. I've never read Grassmann and only have an overview-like understanding of Clifford so it might even be pointless rambling. Start with complex numbers: you have a scalar plus a (2D) bivector which acts as a pseudo-scalar and requires one component. Extend to Quaternions: you still have a scalar plus a bivector but it's now a 3D bivector so it acts a pseudo-vector and requires 3 components. This is the source of all historical confusion and the why the 3D complex number equivalent requires 4 values instead the expected 3. Gibbs and Heavyside jump in an and are only interested in the bivector part of the quaternion product. Given two bivectors A and B then their product (in quaternion-speak) is 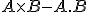 . The minus sign of the dot product portion seemed pointless so they drop it and change the signature of that of (what's now) a vector. The source of the minus sign is that the product effectively adds angular information and they were interested in relative (angle subtraction). So they really wanted 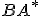 and not 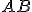 . Since there are more than one inner/outer product pairs definable for Quaternions, which are you referring to (I probably could have deduced by context but I'm too lazy). |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #37 on: July 28, 2014, 12:22:20 PM » |
|
As I suspected , Hermann and Robert develop the closing in product in the 1862 Redaction and completion of the 1844 work, if it could ever be called complete.
Perusing the Index to necessary or needed " art expressions" and their full explanations I notice that Strecke now makes a late entrance into the system, replaced by Stüfe and Grôße as fundamental building blocks in the system..
There are a number of products and multiplication processes of which the Aussere and the Innere are the main concepts . The mixed product also is introduced.
While this redaction undoubtedly saved the work from obscurity, it's main fault being its obvious incoherence in 1844, nevertheless it represents a substantial concession by Hermann to Robert who was a classically trained mathematics teacher and a rising star in the district.
It is perhaps well to remember how Hermann came to his Förderung via Strecken rather than through Number or Zahl. Hermann links directly to book2 of the Stoikeia.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #38 on: July 28, 2014, 03:00:36 PM » |
|
Thanks Roquen. All contributions to the thread are welcome.
As I recall Hamilton was a chief advocate for a sub field of Mathematics called Algebra or symbolic logic and symbolic arithmetic. Algebra was developing through the higher arithmetics dealing with polynomials , power series inductive logic and much more. His impetus besides Aristotle, Newton and a relentless uncle was a friend who was humiliated for exploring the imaginary logarithms as they were then called. So in 1831 he published a paper on conjugate couples or the Science of Pure Time.
This landmark paper was a vehicle for the mathesis or mathematical doctrine of the imaginaries. Using a set of abstract moments in time he developed the ordinal arithmetic of a single moment, then a couple or a beginning and ending moment. His main sounding board against whom he measured himself was LaGrange and he cleverly develops a mathematics supposedly not based on length! However despite its brilliance that proposition fails in that he has to resort to a notion he freely calls a step which is an analogy for a time step .
So, in some quite wonderful mathematical prise he develops arithmetic up to the level of higher arithmetics and logarithms and trigonometric ratios. He does so in a single lineal progression on the assumption that time progresses one way, but our minds conduct us in either direction in time! He uses a ellipsis to go from ordinal " numbers" to cardinal numbers, and similarly he uses a complex conjugate differential relationship, in which he slips the orthogonal axes without justification to develop the rules of the imaginary functions, which after he reduces to "numbers".
At the end of this tour de Force he was able to justify his friends assertions re imaginary logarithms, and along with Boole to raise the status of Algebra as a subject. He thus managed to annoy many establishment Mathematicians who went gunning for him. When he eventually revealed his concept of the Quaternions he was riding high socially and internationally, but Kelvin and Lewis Carrol waged a campaign against his" nonsense" mathematics.
Grassmann on the other hand was struggling to find time to put his ideas and insights into a coherent whole! Eventually in 1844 he published what he had in the midst of great doubt and indecision about whether he had done a good enough job. It was not good enough and was rejected by the mathematical and philosophical establishment in Prussia. However it gained a small and influential Audience internationally and sparked off a revolutionary subculture with surprising consequences.
By1862 he had refined the ideas and presentation enough to gain growing respect in Prussia, but puzzlement in Britain and America. However Bill Clifford got it, as did Hamilton years before him. Gibbs however did not. He could not understand the multiple Algebras but made notes any way, which combined Hamilton and Grassmann ideas and notations, but avoided the imaginaries.
As a Protogé of Kelvin, his notes became a chief weapon in diminishing the influence and acceptance of Hamoltons Quatsrnion vector concept in American universities. Kelvin also forced Maxwell to abandon his acceptance and promotion of Quaternions. Thus Hamilton was marginalised by his peers for daring to go against the establishment.
This historic battle has lead to many confusions at the basis of the modern notation you are now using. It is these fundamental confusions I am investigating so carefully.
|
|
|
|
« Last Edit: July 29, 2014, 07:27:35 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #39 on: July 29, 2014, 08:13:18 AM » |
|
It never ceases to amaze me how naive my assumptions are initially, but that is a good thing.
When looking into fundmental issues it is best to start as a little child. So for example I recall Gauss publishing his ruminations on the imaginary quantities in 1830 in haste, after finding a forgotten 1817 paper by Wessel in which he set out his theory of Directed Numbers. At the time Cauchy, Argand and others had been working on applying these strange adjugate quantities in France, but everyone was edgy about their metaphysical credibility , and Gauss was no exception.
Soaring above these workers were the ideas of Newton, Sir Roger Cotes and DeMoivre and of course ! I will add Euler to this list of Sublimes because they fully worked out the major conceptual base of the mathesis of the imaginaries.
Historically then we have a divided corpus of philosophers and practitioners. The sublimes saw what had to obtain, but try as they might they knew their contemporaries would find it hard to understand. Then the followers on like Gauss and LaGrange attempted to grasp the " reality" of these concepts rather than the sublimity or unreality of them. That these were formal constructs of the mind was not sufficient!
Eventually Wessel showed a solid , grounded practical use of them that Gauss could understand and he then published his ruminations, and his school claimed preeminence over French concepts, and indeed another claim. They even tried to browbeat Hamilton into conceding Gauss as prior to his 4 component Algebra, but Hamilton was not bullied, and his claim upheld..
The mathematical societies were divided. In Europe there was a willingness to explore these imaginary quantities, but in. Britain and America it was considered crazy Talk! In fact the negative numbers were still an issue at elementary levels! still !!
In 1844 Grassmann barely had time to pick his nose let alone research Gauss and Hamiltons work. However Robert did have time and opportunity to research thses things, and By 1862 Gauss concepts, Rienanns concepts are referred to drectly in the text, although preeminence is ascribed dubiously.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
Roquen
Iterator

Posts: 180
|
 |
« Reply #40 on: July 29, 2014, 10:44:56 AM » |
|
Some historical notes (from memory so don't read too much into it. Probably some of this is in http://www.lrcphysics.com/storage/documents/Hamilton%20Rodrigues%20and%20Quaternion%20Scandle.pdf). The situation is pretty understandable. Prior to Hamilton and Grassmann there were only integers, reals and complex number for algebras. All of which behaved in a similar fashion. Then all of a sudden there are constructs that behaved completely differently and had unexpected structure and the "why" was missing. Hamilton's notation was pretty awful and then Gibbs and Heaviside came along with vectors which had clean notation (taken from Clifford). As an aside I just re-read Coxeter's 1946 "Quaternions and Reflections" which someone twittered an he's still using Hamilton's notation. Now Gibbs (physicist) and Heaviside (engineer) totally focused on practical applications of vector analysis/calculus whereas Hamilton's camp mostly focused on the pure mathematics side. Hamilton even resisted some practical application, as an example Cayley almost immediately formulated a generalized 3D rotation (p' = qpq *) and for years Hamilton only talked about his broken version (I'd have to look the form up). Soon thereafter linear algebra pops up and between vectors and LA applied mathematics had tools they could work with. Applied mathematics always gets the lion's share of attention. The flamewar started between the two camps and Hamilton's group came off looking like crackpots. On Lord Kelvin it should be interesting to note that he was very close to Peter Tait and they wrote "Treatise on Natural Philosophy" together. Tait was in the hotspot of the flamewar, so personal feelings probably have alot to do with Lord Kelvin's dislike of Quaternions. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #41 on: July 29, 2014, 12:17:07 PM » |
|
It is clear, at least to me that the difference in the coherence of the 1862 work to that of the 1844 work represents a maturation of thought, collaboration and confidence in the format for presentation. In that regard I can see the hand of both Robert and Hermann.
As a successful publisher Robert had a clear editorial view.mit is his critique of the 1844 version which lead to Hermann bndoning his stated plans for the 2 volume versions and melding the ideas together into a new single volume presentation that was coherent. It was Robert who stated the 1844 version contained a difficulty which mathematicians could not overcome, and thus the work was more for the classically prepared scholar of Philosophy who had studied the Latin versions of philosophy! Ordinary mathematicians just were not going to get it, in addition to their dread of philosophy.
Robert also had another agenda of his own. He was highly critical of the non scientific basis of Philosophy in general, and his aim was to reveal that basis as flawed and to replace it with a scientific one that his father Justus, and others and he was developing. This was to be his master work and he needed Hermanns work to be well accepted so as to promote his own similar philosophical ideas.
Since Pythagoras it has been known that there are 2 descriptions of the world of conscious experience. One is as a collection of forms in space, the other is as a huge universal mosaic of monads. Plato and Socrates playfully added another important element to the experience: is it real or is it a shadow? This is the Platonic theory of Forms/ Ideas.
These distinctions have characterised philosophical debate and exposition ever since. For example Dedekind starts with the notion of ideas in developing his concept of Number in his famous Essay explaining the Dedekind cut. Hertz in his treatise on mechanics starts with a distinction between images and what is sensed, and how we must choose those experiences whose sensory image is invariant as our notion of reality.
Thus any simplistic interpretation of the word or action of geometry is completely misleading. I intuitively recognised this and coined the conceptual word Spaciometry to free my mind. Hermann considered with Robert calling the ideas they discussed Formenlehre, the study or theory of form. However he decided against that because it seemed not to capture the broad range of processes involved in mechanics and mathematics. Certainly geometry would not do as a title since even in Hermanns day Geometry had slipped into a position of low esteem, unjustifiably!
They decided to study the behaviour of extensive magnitudes(Ausdehnung Größen), a philosophical concept perhaps highlighted by Descartes, but debated by Leubniz and Spinoza vociferously. At the time Kant had managed to broker a kind of peace between the warring philosophical schools who saw in his defense of pure reason a solution to their issues. Reason at the time meant belief in the Divine reason from God, not our scientific rationality or Logical positivism of today, which classes that Reason as irrationality!
The extensive magnitudes are experiences, but how do we determine real from shadow? Hermanns Hegelian dialectic solution was that we keep both distinctions and work them together and see what comes out as a product! This is the Hegelian dialectic process, which is a version of the Platonic dialectic process. However Hegel's dialectic is notably different and extremely logically rigorous in a geometrical / spaciometric way. It make full use of the Euclidean philosophy of the Stoikeia to describe our experiences whether real or Formal. Formal here means having an idea/ form in the platonic sense, while real represents a decision outside of the rules of the Socratic/Platonic game.
In one sense today we acknowledge the impact of more than one sense on our experience. The Socratic game is essentially visual. Thus we can define real as the other sensory modalities of a form experience. Hermann defines it in behavioural outcome terms. Something is real if you can't step over it! Similarly something is formal if no matter how you try you can't bury the concept or make it disappear!
We can go back to Apollonius to get a clear picture of formal Spaciometry. It is in his studies that multiple geometries are revealed each dependent on the form analysed. It was also his method of studying these geometrical forms that is "geo" on the ground "metry" measuring and counting and ordering , that lead to coordinate geometry . But the genius of Descartes in promoting this idea as a paramount method is all we ever hear! In fact it was Wallis who established the coordinate frame we know and love to hate!
From this coordinate geometry / Spaciometry Leibniz glimpsed the possibility of an intuitive algebraic language that would remove the reams of coordinate pairs required to describe a firm and return us to the rhetoric of points lines planes and circles. At a time of geopolitical turmoil no geometers were interested and Legendre seemed to have closed the book on geometrical education anyway.
Despite Gauss concerns about the state of geometrical research, foolishly attempting to prove the parallel postulate, it was not surprising that elementary grade school teachers should explore the difficulties and come up with the solutions. The Grassmanns were in that unique position at that unique time when the Humboldt reforms meant that academia was in turmoil in Prussia and all levels of the educational system were imperially commanded to prepare Prussia for the modern scientific age!
Spaciometry of extensive Quantities , that is bounded Magnitudes, is what resulted from the research of Grassmann and others. That Spaciometry included the study not only of extension but also rotation. It also included a third concept, that of Projection. These 3 form the fundamental transformations of Spaciometry. Klein introduced a term called translation which applies to a form, but it is fundamentally a construct of the three fundamentals: extension, rotation and projection.
Hermanns contribution is his insight into how to notate orientation , and which form to use as a fundamental basis for addition and multiplication analogues for line segment quantities, in fact any quantities of form! The answer was in Book 2 of the Stoikeia of Euclid.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #42 on: July 29, 2014, 02:36:51 PM » |
|
Thanks Roquen. You mentioned Hamiltons broken version. I would like to know a bit more of that if it is at all different to the generally unrecognised action of doubling the angle if Ritation common to all algebraic methods. As far as I know Rodrugues is the only version that recognised the importance of half angles in 3d rotation in the 1840's paper that went completely ignored. However I have not got that far yet in my perusal of Grassmanns analysis. For me the Eulerian definition of the semi circular radian measure as 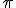 has this unfortunate consequence. Essentially it is a constant error and easily addressed. Hamiltons Quaternions are a brute force version, and there are many quaternion and quaternion 8 groups which are commutative. I devised the Newtonian triples after researching the quaternion 8 groups, and they are commutative and not a quaternion group. They also model 3d rotation but with a twist. In the cubic they seem to give a spaghetti double form . I have not investigated them further as of yet. Complex numbers were and are ever a puzzle. Complex magnitudes how ever have a vibrant Geometrucal analogue, and this is one of the clear statements of Hermann. Later Robert ascribes this insight to Gauss, which is in my mind dubious to say the least. His combinatorial form is a specific example of Hermanns more general philosophical description, which admittedly is incoherently put together, but nevertheless contains brilliantly clear insights. |
|
|
|
« Last Edit: July 29, 2014, 07:01:55 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #43 on: July 29, 2014, 07:11:31 PM » |
|
Roquen thanks for the link which has given me more documented information to correct my statements of historical developments. In particular the later Hamilton who was a troubled man I knew, but his public personae is graphically drawn in the link although just a sketch.
The gloss on Gibbs and Heavyside is a different matter. Much more has to be said about how vectors became dominant through the work of Gibbs and Heaviside as they reworked Grassmanns ideas in relation to Hertz , LaGrange, Ampère and Clifford and Hamilton.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #44 on: July 31, 2014, 11:06:51 AM » |
|
The Stoikeia of the Euclid school is an introductory Pythagorean philodophy course at undergraduate( below Mathematikos) level. Over the years since its first draft it has been used in the Euclidean Platonic Academy by many great teachers but apparently Apollonius is the main critical redactor of the course that we have documentary evidence of. Only a part of his philosophical treatises have come down to us, but it seems clear that his work on Conics substantially improves on that of Euclids own. Conics would be an advanced course perhaps requiring the qualification of Mathematikos, I am not sure. There are several other treatises of the Euclidean Platonic Academy that may also have been required to obtain that qualification including Optics and Data, to specify but two . It would appear that Apollonius felt that students or discoursers were ill equipped to properly understand Conics because the philosophy of the circle and sphere was so obscure in the Stoikeia. His recommendations infuse a greater emphasis on the properties of the sphere and circle into the Stoikeia and probably our extant versions contain these redactions of his. In Book 2 of the Stoikeia we are introduced to the Gnomon. Without elaboration the gnomon is approached in terms of quadrilateral rectilinear forms which are constructed by rotating line segments. Thus the gnomon consist of the rectilinear form and a necessary curved form that is associated to the rectilinear one. I called this the curved Gnomon. In fact it is usually called a sector, and all rectilinear quadrilaterals have an associated sector used to construct them. As a consequence there is a parallel development of metrication( counting multiple forms) between rectangles and sectors, and many basic formulae have the same format. Given a line segment AC cut internally at a point B the rectangle AB BC is constructed by rotating one of the internal segments by a quarter turn. As that segment turns it scrapes out a quarter disc . That shape and the segment not turned forms a curved gnomon. The rectangle half perimeter could be considered as a limit Gnomon, but in practice the gnomon consists in the thick form that results from rotating a carpenters ruler. The rectangular gnomon defines proportional relationships between all parallrogramic forms, but the basis of this is the proportional relationships between the circles that share the diameter of an enclosing circle that is tangential to them. Kissing circles if you will. Thus the gnomon proportions are stated in terms of the diameter of the parallelogram, the longest diagonal. These proportions hold for the shortest diagonal, but then the circles do not enclose the rectilinear form also. In passing I must note that even the notion of rectilinear is defined by dual ( iso) points obtained by intersecting arcs . I frequently rehearse how this is done from 2 arbitrary points in space whose displacement remains fixed by our decree or relativistic observation. The gnomon resurfaces in the concepts of Grassmann as the parallelogram product. But it is the summation form that is the real innovation. The summation form is based on the translation by a lineal projection of a parallelogram. This translation forms the basis of tessellation of a space. It requires parallel line translations , or extensions.. We call these parallel projections today. Grassmann did not recognise this until he was working on the geometric products in the plane. In the one form he noticed both his concept of a product and his concept of a summation. Later it is noticeable how he mixes this notion of a construction product with the notion of arithmetic multiplication. This is not an obscuration, but a revelation. However the concept of numbers does obscure this process, as currently taught. The curved gnomon is clearly not presented in these early Grassmann notes. In fact the curved gnomon is a development that Euler promotes as his radian measure. I could go back to Cotes, but the clearest presentation , and systematic development is given by Euler. The consequence of the curved gnomon for Euler was the exponential functional relationship with the imaginary quantities. Both Grassmann and Cotes Realised that this was geometrically analogous to the arc. This related the arc to the swing of a line segment . The swing of a line segment carves out a sector. That sector is the curved gnomon. However Grassmann encapsulates this in a rhomboidal form, and so brings it right back to a rectilineal parallelogram! The curved Gnomon is within the Lineal Algebra, which in itself demonstrates that the formulae will be analogous. However, the curved gnomon is a more advanced philosophy as Apollonius demonstrated. The nearest we get to it today is in Spherical geometry and spherical trigonometry. Norman Wildbergers universal hyperbolic geometry is the best course I can recommend in this area. It will be noted that notions of perpendicularity has to be generalised to make consistent headway. It is this important Pythagorean principal that is key to the curved gnomon, and the advanced conceptual difficulties encountered . Despite Eulers clear exposition,the full understanding of the curved gnomon lies in the Newton, DeMoivre, Cotes work and theorems on the roots of unity, and ) . Euler, Hamilton, Gauss and Grassmann in short order have to grapple with these concepts so clearly delineated by Newton Cotes and DeMoivre. Grassman however has a notational technology that cuts through the confusion of concepts to help express these basic notions of trigonometry more directly and simply than any other. |
|
|
|
« Last Edit: August 01, 2014, 06:21:40 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










