|
jehovajah
|
 |
« Reply #30 on: January 30, 2011, 11:29:52 AM » |
|
The sine and cosine and tangent have a suitably well established flip algorithm supported by the Bombelli operator. This observation actually allows me to rewrite the Bombelli operator in terms of conditions based on π/2 and its multiples. However there is one new relation i would like to explore ^2 ) +sin^2(\frac\pi2-\theta) =(^r\pi 1)^2 <br />) |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #31 on: January 31, 2011, 03:22:08 AM » |
|
"Imagine that 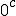 and  are orientations. as are 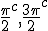 Then sin 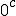 =sin  =0 and sin 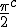 =sin 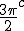 =1 This is because i do not use + or - for sign i use orientation. Each case is clearly distinguished by the orientation! Isn't it? What can i say about sine and unity? I say sine is a 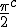 unit for scalar plethoration. Any sine scalar i can denote with a prefix 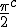 and any opposite sin scalar with a prefix 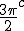 thus i naturally write 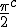 sin sin for trigonometric sine scalars where  is an angle magnitude not an orientation." To clarify among the jumble: i am imagining that sin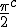 is the magnitude of the unit scalar in that direction. Thus for any direction there is a natural unit magnitude using the sine ratio. is the magnitude of the unit scalar in that direction. Thus for any direction there is a natural unit magnitude using the sine ratio.Now a similar examination of the cosine behaviour gives Then cos 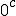 =cos  =1 and cos 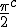 =cos 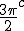 =0 Each case is again clearly distinguished by the orientation isn't it? I can now say about cosine and unity that it is a 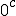 unit for scalar plethoration. Any cosine scalar i can denote with a prefix 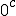 and any opposite cosine scalar with a prefix  thus i naturally write 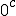 cosin cosin " Again to clarify among the jumble: i am imagining that cos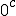 is the magnitude of the unit scalar in that direction. Thus for any direction there is a natural unit magnitude using the cos ratio. is the magnitude of the unit scalar in that direction. Thus for any direction there is a natural unit magnitude using the cos ratio.Thus combining the two gives a combined unit cos 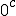 + sin 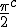 which may or may not have its uses for orientations between 0 and 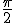 I know this is unfamiliar ground because it is unfamiliar to me, but the flip algorithm helps to specify the process. The flip algorithm governs a procedure of assigning orientations of a measuring instrument and the conditions of the flip to the different orientations of measurement. Allied to the flip algorithm is an aggregation operator, like the Bombelli operator, like the Kujonai operator, Like the Fracmonk operator that controls the aggregation structure ans the aggregation mod() gates,determining when orientations can be flipped to other orientations to enable summation, or the orientation a product or a reciprocal type product flips to . So the flip algorithm is involved in measurment and calculation and it is an if-then procedural algorithm, a conditional statement of operation. Thus i have suggested an orientation notation, now we need to determine a Bombelli operator in teerms of that notation. the addition operator flips are straight forward +mod() 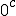 becomes -mod() 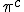 -mod() 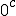 becomes +mod() 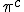 as they say "vice versa". The multiplication ones are also straight forward for integer magnitudes 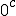 * 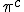 gives 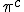 = 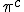 * 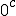 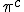 * 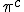 gives 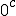 = 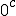 * 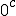 It is immediately clearer how the Bombelli operator is in fact orientating and one may now ask how come? The answer is Brahmagupta when he wrote 1-1=0, and the indian and the greek use of the unit circle in trigonometry. Otherwise using the chinese colour distinction would have meant any distinction could be used to represent annihilating magnitudes, and the +mod() gates indicate a structured arrangement of unit standards, thus mod (1) cannot sum with mod(2) type magnitudes. Multiplication is purely about logical assignment of orientation, but it turns out that the unit circle and the trig ratios provide a geometric construction of the logic which applies it consistently to orientation. This application of the circle to measurement has a very long history starting with the sumero Akkadians and the Dravidians, and for a time was a universal mystical, magical symbol competing with the mystifcal magical spiral. Myth has always been associated with the two forms. However the circle and its divisions into 360 sectors was an early Akkadian Achievement for astronomical measurement. Whatever else the circle as the ultimate foundation for measurement has proven itself throughout the millenia, but it is the spiral that has proved itself as the foundational technological form. Now we know that the circle and spiral are indivisibly linked at a fundamental group structure level. so sin 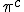 *sin 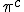 =sin 2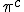 =1-cos 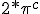 /2=1-cos 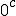 /2 So under the trig multiplication identities we get a similarity in behaviour of the associated angle magnitudes, and this subtlety is enough to signal the fundamental symmetries involved in this type of attribution. This is a case of prosthphaeresis and links directly to logarithmic and clock arithmetic behaviour of the trig functions. Modular arithmetics and congruence relations,symmetry and relativity, self similarity and logarithms all arise naturally out of the trigonometry of the unit spherical surface, and hyper geometries lie just beneath its surface. To my mind Cotes saw this and made it his aim to study it fully. I have explored this by way of exercise, as i much prefer the radial r and circumference c notation. I hope that the structure of the flip algorithm in it 2 parts is clear and the ease in which it may be used is clear. I hope also that it is easily seen how the Bombelli operator is adapted to this notation, and why the trig relations are a model of the rules, and indeed how this may be generalsed to both Kujonai's operator and to Fracmonks. If i get time i will do the exercise for Kujonai's operator to show how i got the images posted in the gallery under his name. |
|
|
|
« Last Edit: January 31, 2011, 12:02:52 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #32 on: January 31, 2011, 09:29:38 AM » |
|
http://upload.wikimedia.org/wikipedia/commons/4/4c/Unit_circle_angles_color.svg " This is space ,Jim...but not as we know it!..." " This is space ,Jim...but not as we know it!..."Thanks jim If you remember CAST you will know the old fashioned flip algorithm related to the positive sign All in the first quadrant Sine in the second quadrant Tangent in the third quadrant and Cosine in the fourth quadrant. The inherent and powerful symmetry lies before your eyes! Imagine now a dynamic version of this using a colouring algorithm. Realise that De Moivre hit upon the unique power of this space, the unit circle wraps all the reciprocals of its oriented magnitudes within itself. They are not within the disk or outside the disk, but precisely in the circumference of the circle. Thus this impossible space is an infinite infinitesimal dynamic system which is unstable and unpredictable and able to implode or explode, through the slightest variance. So in the sphere's surface we have that infinite possibility surface which dynamically generates all fractals from the Cosmos to the tiniest wormhole, and beneath its surface is Hyperspace! "This is space ,Jim, but not as we know it" is based on a quote from Startrekkin across the universe.
<a href="http://www.youtube.com/v/OrYbkbWRA2I&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/OrYbkbWRA2I&rel=1&fs=1&hd=1</a>
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #33 on: February 02, 2011, 06:55:26 AM » |
|
The basis of the Bombelli operator is found here on page 18. It is rendered amazingly simple by this treatment to give a trig meaning to √-1 and to found the complex numbers securely on these trig relations. I might also add that of course i have discovered nothing new, just cleared away the mountain of confusion covering these simple observations! One fancy i have is that Newton absolutely based his 3 laws on these trigonometric relations particularly those of spherical trig, and that the first law states conditions of dynamic and static equilibrium, not in terms of straight lines but in terms of tangents to a curved motion! In other words he had in mind the trigonometric relations of the tangent to the unit circle underpinned by the sine and cosine ratios. His third law details the nature of static Equilibrium, and his second law details the nature of Dynamic Equilibrium, in which force or pressure arises only as a means of maintaning equilibrium in a dynamic state. Having achieved Equilibrium forces disappear but motion continues forever! Thus Newton describes the laws of a Dynamic Motion field in which constant motion everywhere is immediately assumed. Action at a distance therefore is not a mysterious force, but a relative point of view in a dynamic motion field. Newton understood that, but wanted to find out the true state from God's point of view. This he found impossible to conceive and so declared all a mystery. We accept the conundrum as a fundamental outfall of relativity, which was only possible because Einstein had no qualms in placing God inside the reference framework. Thus God had the same undecidability conundrum as a human observer, and the problem goes away! Of course that has consequences for a theory of God, but that is for theologians to sort, not scientists! |
|
|
|
« Last Edit: February 02, 2011, 07:35:05 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #34 on: February 02, 2011, 10:47:45 AM » |
|
Using these products we can define√-1*√-1 as √(cos π*sin3π/2) |
|
|
|
« Last Edit: February 04, 2011, 12:18:42 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #35 on: February 03, 2011, 10:42:03 AM » |
|
I am actually a bit annoyed at mathematicians over last the 5 centuries! The simple and obvious conclusion on investigation of complex numbers is that they represent the algebraisation of Spherical and Plane trigonometry, the calculation part of Geometry. Any mathematician, and particularly geometer who has not used or referred to the use of complex numbers in the proof of certain geometrical theorems or facts, has not advanced very far in his subject. But what is particularly galling is that having noticed this use i have not heard anyone explain that the formal equivalence of the two needs to be expounded from the very outset of education in trigonometry! There are of course historical reasons, the main being the rivalry and secrecy between Cardan et al, ".....It is unclear exactly how Bombelli learnt of the leading mathematical works of the day, but of course he lived in the right part of Italy to be involved in the major events surrounding the solution of cubic and quartic equations. Scipione del Ferro, the first to solve the cubic equation was the professor at Bologna, Bombelli's home town, but del Ferro died the year that Bombelli was born. The contest between Fior and Tartaglia (see Tartaglia's biography) took place in 1535 when Bombelli was nine years old, and Cardan's major work on the topic Ars Magna was published in 1545. Clearly Bombelli had studied Cardan's work and he also followed closely the very public arguments between Cardan, Ferrari and Tartaglia which culminated in the contest between Ferrari and Tartaglia in Milan in 1548 (see Ferrari's biography for details)....." http://www-history.mcs.st-andrews.ac.uk/Biographies/Bombelli.html Bombelli himself was not open unil he had published, but then again he was not a mathematician but an engineer and probably felt intimidated. Bombelli is so crucial to this whole subject because he publicly announced that he used the Greek methods to solve the problems. I was unaware of the history of Spherical trig until i explored this topic, but now i am aware i am annoyed! I did introduction to trigonometry when at primary school! Admittedly analytical trig was too advanced for a 10 or 11 year old in general, but ratios are not, neither are scalars or navigation etc. I believe the mystical and the mythical plays its part in all sciences and that includes mathematics! The mythical √-1 has generated an alternative mathesis - methodology- of dealing with trigonometry namely the complex numbers, and in addition: vectors, a derivation from complex numbers right at the start. This may not have happened as it did if this "mystery" √-1 was not promoted to mythical proportions! However there is no longer any need to be ignorant of the simple truth that trigonometry and trigonometric concerns underly, underpin, and found the notions of complex magnitudes and vectors. This leads to a direct relevance of Pythogorean concerns about unity; an inestimable disproportionate impact of Eudoxus' proportional theory; the importance of distinguishing arithmoi from unity; the plethorate nature of measurement as aggregations of unity; and the Shaping effect on all of mathematics of Euclid and Plato! Though one is eager to admit all sorts of sources to mathematics, Indian and Chinese in particular, it cannot be avoided that by conquering "all the world", Alexander the great lead a dominant and impressive cultural campaign called Hellenization, that influenced scholars in India and China and reflects back echoes in mathematics to us today. Chief among these influences and collaborations was and is spherical trigonometry and its application to astronomy, astrology, and the building of great monuments and temples and all artistic endeavours. Somehow the introduction of Brahmagupta's "negative" numbers confused the plot, and got lost in translation by Arabic intermediaries. We end up with Bombelli who rhetorically introduces notation ±√- and mathematicians lose the plot! Descartes grumpily calls them imaginary, while others scratch their heads in bewilderment. Nobody connects geometry with geometry, nor later, trigonometry with trigonometry! Geometrically "meno" was associated with the rotation through π anticlockwise, thus with the circle theorems of Euclid and the Trig of Euclid. No one thought to give π/2 rotation a sign other than the perpendicular sign of geometry, and that is where the connection fails! If Bombelli had gone that one step further in his madness and put | or even 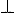 we would have had no difficulty in drawing on the insights of trigonometry much sooner. √- √1, or √-√a for the general case is what we have been looking at all this time. meno di meno and piu di meno are the whole sign. We do not do square roots of "negative" numbers we do square roots of Directed numbers! The signs give us the directions and +√- is the perpendicular direction 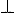 anticlockwise, but also the clockwise 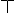 is -√- . Everything else is trigonometry as well! |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #36 on: February 06, 2011, 02:01:59 AM » |
|
I have been able to demonstrate the trigonometric basis of the complex "numbers". First we need a spherical trig grapherSecondly we need to make clear some conventions. Angles are measured anticlockwise. The minus sign will be used in the normal sense, but will not be used to alter aggregation, nor in a Bombelli type vector or operator, it will be rarely used and means opposite direction of "motion" rather than orientation. The The radials move away from the origin of the sphere in a positive direction . Moving in a negative direction is moving toward the centre and out nto the radial in the π radian "positive" orientation on the other side of the centre. The square root of a magnituse includes a dynamic reorientation of the radial of the magnitude by π/2 radians. The complex "numbers" are therefore representative of aggregations of the form of spherical polar coordinates, namely 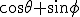 , where  and 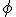 have the condition that they must always be measured orthogonal to each other. Now, of course , the app uses the negative sign through and through, however the calls the formula makes do not involve calls to complex arithmetic , and the formula at least can be written to remove reference to even negative signs, so that only addition and subtraction aggregation are referenced. In addition i have to set phi to run from -1*π to 0 radians so that the app is drawing anticlockwise angles through and through. The iteration(4 stages) (0.4*(0.5*(0.12*(1.07*(cos(s)+sin(t))^2+cos(1.05*pi*s/s)+sin(0.5*pi*t/t))^2+cos(1.05*pi*s/s)+sin(0.0*pi*t/t))^2+cos(1.05*pi*s/s)+sin(0.5*pi*t/t))^2+cos(1.05*pi*s/s)+sin(0.5*pi*t/t))^2+cos(1.05*pi*s/s)+sin(0.5*pi*t/t) is based on 1.07*(cos(s)+sin(t))^2+cos(0.0*pi*s/s)+sin(0*pi*t/t) = (1.07*( 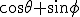 ,)^2+c) Which is a spherical surface(1.07*(cos(s)+sin(t))^2) + some variation with a constant translation(cos(0.0*pi*s/s)+sin(0*pi*t/t)) along a specific radial. The surface is just outside the unit sphere surface. Non of these scalars make much difference to the surface drawn, but they do affect closure of the surface. It is recursion/ convolution that makes the difference. This literally means the relational properties of the surface are altered not by scalar but by convolution. We naturally count the end product of each convolution as an iteration. I suppose the most accessible analogy is that of the specific marque of a specific form of a car take the Ford fiesta, or the Volkswagen Beetle. Each vehicle is convoluted, much recursion goes into producing each iteration. And of course, recursion is about bringing together things into a relatonship that is detailed and complex. We take for granted the convolutional power of a modern graphics system, able to compute the position of each of millions of points/pixels directly or relationally. You will notice that at each iteration i have reduced the radial of the surface that is being convoluted. This has been done by trial and error, which is how i discovered the required ratios. You should play with them and with increasing the number of iterations. Directed dynamic magnitudes therefore have dynamic trigonometric ratios of the most complex convolutional relations, and we can now draw these relational convoluted surfaces, that is tensors, with utmost ease nowadays. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #37 on: February 09, 2011, 12:31:32 AM » |
|
The plane trig basis for the complex numbers is equally demonstrable First the plane grapher is set to polar coordinates. Then the following relation is iterated: (1*cos(pi/2+4*t)+1*sin(1*t)) (1*cos(pi/2+4*t)+1*sin(1*t))^2+cos(pi/3)+sin(pi/2+pi/3) is ^2 +c) (0.2*(2.9*(0.081*(1*cos(pi/2+4*t)+1*sin(1*t))^2+cos(pi/3)+sin(pi/2+pi/3))^2+cos(pi/3)+sin(pi/2+pi/3))^2+cos(pi/3)+sin(pi/2+pi/3))^2+cos(pi/3)+sin(pi/2+pi/3). There are so many things to vary with different outcomes that these truely deserve the name complex. I have a issue with the term "number", and much prefer the term scalar. The indians were the first to develop the sine ratio! before them the ancients and the Greeks used the Chord. For me the chord is more intuitive and suggestive of navigation measurement and orientation. However logarithms and prosthaphaeresis may not have been so obvious from the chord. The other thought that occurred to me is that Brahmagupta may not just have been stating the obvious when he wrote 1-1=0 He may very well have been thinking co-sin(π/2+π/2)- sin π/2= 0, before the cosine was seperately figured. The cosine was undoubtedly used as the sine(chord) at right angles to the direction of initial measurement of the sine(chord). |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #38 on: February 19, 2011, 02:50:06 AM » |
|
It seems a moot point, but since these things are so clear in Euclid and Ptolemy it is hard not to think that Brahmagupta, and Bombelli, both saw the behaviour of the trig ratios and derived the dehaviour of directed numbers from them. The unique insight of shunaya allied with the greek insight on unity seems to be evident in Brahamagupta's collected work. and Bomelli certainly accurately described the rules for multiplying by √-1. There is a further directional element to addition and subtraction the aggregation/ disaggregation proceses: Aggregation tends to be a gathering to a central location. That is aggregated objects move in the opposite direction to the positive direction of the ray of orientation. The Bombeeli operator covers over to directed motions: translation and rotation, both accessed by the "multiply" command.So these notions of directed motions in the actual operator definition are to be explored. Bombelli's use of the word "via" for multiplication needs to be referenced against the gnomon. So very much in keeping with the practical nature of greek geometry the gnomon would be used to "establish, hold, support, represent, define" a rectangular "area". The 2 sides of the gnomon would be designated "via" which is of course " road, way, direction, route"and as a preposition "by way of, or by; but not as in 'near' ". Thus an area was "calculated" by a gnomon. Literally it was measured by the "via", ordered and arrayed by the "via", and the "calculii" (latin) the stones of "reckoning" counted. Thus geometrically multiplication was an ordered rhythmical iteration described by the 2 via of a gnomon. Physically the iteration would result in a tiling or stacking, and the tiling would proceed in a "via", each "row" beinc thought of as a single unit. Thus one of the via becomes a row the other may be termed a via. Similarly, one of the via may be termed a column and the other a via. Bombelli's operator shows that intuitively he thought of these via as having a direction, which he called "less" or "more". He intuitively as did the greeks associated dynamic magnitude with a direction or if static , an orientation. So how do we describe the second notion of motion in via? Somehow, both Brahmagupta and Bombelli could intuit a curved via, a circular one. I do not mean to egg the pudding, as for thousands of years astronomers and scientists had been relating the curved via of the heavens to geometrical observations, but what Brahmagupta did in the first instance, under i think greek influence as in the case of Hipparchus or Ptolemy, along with some chinese notions, was to relate direction to the circular via in a multiplicative way. The only way this makes sense is with a notion of 0 (shunaya) and a notion of Ptolemy's chord relations. It becomes even clearer (as mud gets clearer!  ) when you drop to the 1/2 chord ratio we call sine, but the indians who first did this called "limb"(?). From spherical geometry and trig it became clear that "multiplying" these ratios, that is swinging around the centre via the circumference usisng the radius as a "row" gave a calculable result. Thus rotation of the radius was a via as well but was subtly different. Only Brahmagupta went on to explore this difference philosophically as Shunaya. sin(x−y)=sinxcosy−cosxsiny sin(x+y)=sinxcosy+cosxsiny 2sin2x=1−cos2x Were all derived by Ptolemy in chord form. Thus π/2 forms a natural and ubiquitous distinction in the theory of circles and the multiplication via a curve. |
|
|
|
« Last Edit: February 19, 2011, 08:51:43 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #39 on: February 19, 2011, 09:45:35 AM » |
|
The notion of "multiplying" via a gnomon leads to the measurement of "area". By this i mean that we are measuring area not as it seems "multiplying lengths". This "operation" of multiplying is an abstraction from measuring a rectangular area. It seems odd to point this out as multiplication is usually taught as "giving" an area or a volume etc. However as an immediate geometer, i have no qualms with dispensing with the abstraction in favour of what is actually happening in front of my very eyes and self. In this way geometry is very empirical and natural and does not need to be thought of as complicated at all. Now how i explain what is happening or what i do to get a result may be very complicated and complex, but that does not make the geometry essentially complicated or complex, only my procedural basis for measurement, and my"method of discourse" . These if anything are what turn childs play into a horrible agonia called mathematics! So a gnomon is used to measure an area, so what does a circular gnomon measure? tha area of a circle which by inspection out to be the circumference via the radius or the radius via the circumference. in boh cases this will be too big when transferred to a gnomon. and as it turns out it is precisely half the measurement of the circumference via the radius. Thus Circle area = 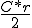 Dynamically the geometry suggests this as correct as whichever "via "you use, triangular variation occurs. Triangles are therefore obviously fundamental in a dynamic geometry, and we get the full set of Euclidean arithmoi as being triangles rectilinear forms reducible to quadrilaterals and circles and of course there solid counterparts the tetrahedra, pyramids, parallelepipeds, polyhedra and the sphere . We have later revisionists and redactors Like Plato et al to blame for any confusion in the basic simplicity of Euclids conception. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #40 on: February 19, 2011, 06:19:45 PM » |
|
Negative Negative numbers, and the equivalent word for negative were introduce by Brahmagupta, a Hindu mathematician around 600 AD. The Latin root of today's word is negare, to deny. The negative numbers, in this sense, denying or invalidating an equivalent positive quantity. The negative numbers were themselves denied for a long part of mathematical history, and only slowly came to be accepted. The first record of the operational rules for what we today call positive and negative numbers came from the pen of Diophantus (around 250 AD) who referred to them as "forthcomings" and "wantings". His work may have been drawn from proposition five in Euclid's Book II of the Elements in which Euclid demonstrates with geometric figures what we would write in modern algebra as (a+b)(a-b)+b2 = a2. This, of course, is easily recast as the more common identity (a+b)(a-b)= a2 - b2. Diophantus would accept negatives only as a way of diminishing a greater quantity, but did not accept them as independent quantities and would not accept a solution that was negative. Al-Khwarizmi (850 AD), whose writings brought Arabic numerals to the west, used a similar approach with negatives allowed in-process but not as a final result. Descartes, around 1636, used the French fausse, false, for negative solutions. Thomas Harriot had described negative roots as the solution to an alternate form of the equation with the signs of the odd powers changed. Today his idea would be expressed by saying that the appearance of -c as a root of f(x) was only to be understood to mean that c is a root of f(-x). In Mathematics: The Loss of Certainty, by Morris Kline includes the following argument against negative numbers by Antoine Arnauld (1612-1694), mathematician, theologian, and friend of Blaise Pascal; "Arnauld questioned that -1:1 = 1:-1 because, he said, -1 is less than +1; hence, how could a smaller be to a greater as a greater is to a smaller?" Franz Lemmermeyer wrote in a posting to the Historia-Matematica newsgroup that Gleanings from the History of the Negative Number by PGJ Vrendenduin suggests that a number line with both positive and negative numbers could be found in the work of Wallis (1657)[This is certainly true as seen here]. Another posting to the same list quoted Kline's "Mathematical Thought from Ancient to Modern Times": "Though Wallis was advanced for his times and accepted negative numbers, he thought they were larger than infinity but not less than zero. In his 'Arithmetica Infinitorum' (1665), he argued that since the ratio a/0, when a is positive, is infinite, then, when the denominator is changed to a negative number, as in a/b with b negative, the ratio must be greater than infinity." Even as late as 1831, De Morgan would still write that one "must recollect that the signs + and - are not quantities, but directions to add and subtract." [ Albrecht Heeffer refutes this position, held by Kline and many others, in a post to the math-history list. ] In a recent book by Gert Schubring see clips here he also supports a view that Wallis' understanding of negatives was much broader than generally credited. According to a post from Laura Laurencich, the Incas had a method of indicating both positive and negative numbers on their quipus as documented by the Jesuit Priest Blas Valeria in 1618." And Bombelli was of course very inspired by Diophantus as was Fermat. But it is clear that Wallis was inspired by Brahmagupta.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #41 on: February 19, 2011, 07:52:05 PM » |
|
It is a surprisingly simple misdirection, but one which bears revealing. There seems to be little evidence that the greeks ever sought the "square root" of much at all. Their concerns were different to those of the Arab Al Khwarzim the patron of algebra and the Algorithm. In fact the word square is a late gloss on Exquadrataeia which explains why so "quadrature" is so heavily used in early writingIf anything the greek had a love affair with the right triangle and developed all rectilinear forms, (arithmoi) in respect of that fundamental. Greeks were no stranger to bits of string stretched tight or knotted in certain ways, Gnomon from which they referenced gonia- a kind of gnomon based on various crossed lines not "Kathetus" that is perpendicular. The circle and the inscribed right triangle or cyclic quadrilateral seems to have been their ultimate analytical device from which they derived their form of complex magnitudes namely trigonometric ratios, especially on the theory of Eudoxus and Ptolemy. They of course conquered all before them both physically and geometrically and had theorie of the conics and spirals and decimal aggregation structures long before others even thought of them. Unfortunately Al Kwharzim, appears to have been more impressed by indian than greek presentation, and it is indeed beautiful, but his presentation obscured the everydayness of greek exposition with the mystical subtlety of the subhasutras. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #42 on: February 20, 2011, 01:45:38 AM » |
|
Even though i have come this far with the notion that somehow √-1 means a rotation by π/2, i am not afraid to ask if the whole idea of rotation is spurious with regard to the complex numbers C.
I can justify rotation around the unit circle as arc lengths on the great circles of a unit circle and the consequent trig relations reflect that but the √-1 seems a bit arch.
From the point of view of gnomon values i can justify the square root as being a geometrical mean of the rectilinear form expressed as a rectangular form. Apart from direction of the row of the gnomon there is essentially no difference in the construction to find the geometric mean of a negative area. In gnomon terms the roots are a pair+1 and +1 or +1 and -1 and the question of the (√-1)2 does not arise as the geometric mean is the same. But there seems to be a unique arrangement of the geometric means so that multiplying them out gives me Bombellis operator, and this requires rotation by π/2 of the geometric mean!
Now if i use curve or trig ratio values values the chord of positive length one occurs at arc π/3 and the chord of negative length one occurs at 5π/3. can i find a root of the chords that necessitates rotation?
|
|
|
|
« Last Edit: March 19, 2011, 05:26:35 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #43 on: February 20, 2011, 08:49:39 AM » |
|
At last I have come to the place where the shaping of trigonometry was done. It is an amalgam of all knowledge skilfully blended but not faithfully transmitted to the west due to religious intolerance and book burning. Therefore westerners have developed many erroneous ideas including the notion of false or imaginary magnitudes. In addition Arabic predilection dictated the mix of information style and method in trigonometry for a long time, but despite looking Indian trigonometry is essentially Ptolemaic. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #44 on: February 21, 2011, 06:48:49 AM » |
|
This is something so simple that it at first seems silly. The geometric mean of the 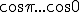 line is the  ...sin(\frac{3\pi}2)) line. Thus 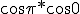 = ) or ) or *sin(\frac{3\pi}2)) Now that makes the quadrature of the directed lines [-1,0), and (0,] have a curious link with trigonometry and in particular the area -1*+1= -1 have some strange "roots". This type of development shows how historical changes can have a confusing effect on later generations of mathematicians/scientists/artisans. We can write 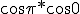 = ) which would be correct except for signage. This thus represents a comparison and an "Aequalis"of magnitude. Similarly for ) Thus the correct relation is 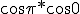 = *sin(\frac{3\pi}2)) Howeve this does not notationally allow us to "square root" but is the correct geometric mean of the line[-1,+1] Geometrically, by Euclid we have to choose ) or ) While this appears a difficulty over signage to us it represents the exact meaning of the calculation/construction. Thus i can conclude that the problem is our modern angst over notation rather than meaning. It is quite clear and fundamental that the signs are not there for their own purposes, but to represent direction. The symbolic choice of + and - for both direction and aggregation was destined to confuse and does confuse. Apparently even Euler was confused by it, And Descartes contextualised the operations and constructions so geometrically that he never got confused by it, thus his term False numbers for negatives and imaginary for roots of negative values. He avoided the confusion not the utillty. Wallis, Newton, De Moivre and Cotes and possibly De Fermat all followed Descartes in this. They were strong and gifted geometers! Al Kwharzimi was the one who introduced the term root or radix into the algebra he created, and he applied it to binomial equations. Thus he maintained a solid link with the geometrical solutions for finding the geometric mean. However later scientists pushe on to cubic and quartic polynomials, but retained the use of the word root and its geometrical association. It was Bombeelii, and then Descartes who publicly showed the use of the geometrical constructions as relevant to solving the roots of many equations, But nobody liked or understood the signage especially the "evil" negative numbers! What we have been left with is the revulsion of past mathematicians, scientists and artisans over the changes to their beloved and familiar "numbers", and their total disbelief in the negative numbers, despite their utility. This was indeed like Alchemy, Magycke, and Divination, the work of the devil and the Moor, and fit for what? To be Burned! No wonder the arabic empire saw Europe as a dark and Backward place, full of superstitious nonsense, and unenlightened by the wisdom of Allah! Fortunately for us a few brave souls struggled on to disseminate the knowledge of the Arabic empire to those who would and could listen, Watch and learn. We are our Father's children, but someday we must grow up! The basis of our dynamic magnitude system is Arabic Indian Greek trigonometry. |
|
|
|
« Last Edit: February 21, 2011, 08:10:42 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










