|
jehovajah
|
 |
« Reply #15 on: January 20, 2011, 12:07:28 PM » |
|
I am now fascinated by the interplay and relationship of Roger Cotes, Abraham DeMoivre and Newton and John Napier. These four are the Britsh Scientists that shaped the Face and heart of Mathematical Science as we know it today. Had Cotes lived we would have learned a thing or two! I believe Cotes was working on a foundational revolutionary Theory of measurement. In every way he reminds me of Albrecht Duerer who combined the Measurement theory of his day into his major work, and spotted the importance of the cardioud curve for natural description. Cotes spotted the importance of the logarithmic spiral for natural description, and his only major work was on Logarithms. But the four of them laid the foundation for vector theory probability theory, Mensuration theory,Complex field theory, computation theory, Tensor theory, Analytical theory. the list goes on and on... The death of Cotes took away a driving force for De Moivre , who had survival concerns of his own, and Newton at this time in his life could not be bothered to explore new realms, So thheir groundbreaking work was shelved, and only parts of it remembered until Caspar Wessel "rediscovered" the obvious and natural and centuries old geometric link which inspired Argand and Gauss and Euler. Wessel deserves his late accolade because he knew from his work with trig and surveying that the Bombelli operator was all about direction "On the Analytical Representation of Direction"
And guess what? He also inspired Sophus Lie. So in short, the work is done. Replacing + and - by orientation markers which directly reflect Cotes innovative radian measure is not only possible it is historically demanded! Cotes Harnonium Mensuram reflects a theory of measurement that goes backto Albrecht Duerer an the 16th century Italian Mathematicians, who are heirs of the Greek Arabic Indian Chinese Axis or network of influence.The simple devising of the radian measure harmonised Spherical and circular trigonometry through the arc. |
|
|
|
« Last Edit: May 08, 2013, 05:03:10 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #16 on: January 20, 2011, 01:41:25 PM » |
|
Some crazy relationships that Cotes an de Moivre noticed i am sure ,as this is par for the course for spherical trigomometry. Sin 0 * sin  = sin 0 But sin  * sin 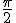 =sin  and sin 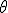 *sin  * sin 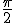 = 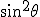 = sin 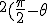 ) - sin( 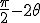 ) in other words multiplying sin by itself tracks the observer around the unit clrcle circumference proportionally like a clock ticking! But this is exactly the process Napier used to calculate his logarithms! What do we have? Crazy! clock arithmetic is related directly to logarithmic arithmetic! And measurements in the 0 orientation have no effect on each other when multiplied through or with sin but measurements in any other directions or orientations rotate each other when multiplied with or through sine! Therefore sine is going to be one of my fundamental actions for orientations as a group, and through spherical trig i hope to explore the group properties of 3d orientations. Of course if i use sine i use or imply all the the trig functions, and all the logarithmic functions and all the arithmetic and geometric series that can be linked to sine |
|
|
|
« Last Edit: January 30, 2011, 11:52:12 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #17 on: January 21, 2011, 10:17:12 AM » |
|
What i love about trigonometry is the crazy whorls of relations it gives! From trig i can see Bombelli operators, Kujonai operators, Symmetry relations , flip algorithms , log like relations, cross product and dot product relations and so vector relations and mod arithmetic relations. This is especially neatly organized by the unit circle/ sphere. In every sense the use of + and - as direction signs is confusing. In orde to remove them i must make clear the use of aggregate gate signs +(mod()) and disaggregate gate sign -(mod()). But before i do look at this Imagine that  and  are orientations. as are 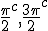 Then sin 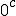 =sin  =0 and sin 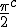 =sin 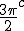 =1 This is because i do not use + or - for sign i use orientation. Each case is clearly distinguished by the orientation! Isn't it? What can i say about sine and unity? I say sine is a 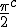 unit for scalar plethoration. Any sine scalar i can denote with a prefix 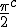 and any opposite sin scalar with a prefix 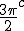 thus i naturally write 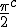 sin sin for trigonometric sine scalars where  is an angle magnitude not an orientation. Now a similar examination of the cosine behaviour gives Then cos 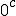 =cos  =1 and cos 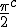 =cos 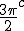 =0 Each case is again clearly distinguished by the orientation isn't it? I can now say about cosine and unity that it is a 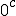 unit for scalar plethoration. Any cosine scalar i can denote with a prefix 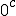 and any opposite cosine scalar with a prefix  thus i naturally write 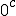 cosin cosin for trigonometric sine scalars where  is an angle magnitude not an orientation. The aggregation structure for these scalars will be as expected Where the +(mod()) gate has not yet been determined but involvrs π/2 in some way, maybe as an angle magnitude. This seems strange , but it is more familiar as cos  + i sin  ! It also highlights the special nature of this aggregation because now it seems simple to inquire after cos  + i sin 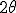 or cos 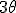 + i sin  etc. I like this draft result because it suggests the way forward. Any one ot any suggestions? |
|
|
|
« Last Edit: January 30, 2011, 11:53:16 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #18 on: January 22, 2011, 10:06:44 AM » |
|
It is good to have imagination, but even better to have premises on which to imagine. Gerardus Mercator has now to be includedin the background story and Newton has to take a pole position! Bombelli and Mercator were contemporaries with Napier. Napier influenced them both including Tycho Brae and Kepler . There are two Mercators so I will clarify later. Napier was inspired by the earlier Mercator and the plight of seafarers in their desire for safe navigation. His method of constructing logarithms applied particularly to the sphere using spherical trig he could formulate calculations for finding position. However the later Mercator was in need of a way to draw flattened maps from a sphere to a plane and needed some way to do this. He eventually discovered the logarithmic series, but not easily. Newton among his early works discovered the logarithmic series, looked at roots of polynomials and welcomed imaginary numbers which means he utilised Bombelli's operator. He extended Descartes rule of signs for finding / calculating the number of root to a polynomial to include imaginary numbers. The ground was set for de Moivre by Newton . De Moivre was able to take Newton's ideas, sketches, geometrical synthetic notions and place them in a new form which would become named analytical. De Moivre did come up with the De Moivre equation before cotes, but that hardly mattered because it had been suggested by Newton before either of them! . Newton's work on the logarithmic series brought crashing together the:- sine, and roots of equations, and series; in the forefront of any student mind influenced by him. De moivre showed how to extract an infinite number of roots, based on Newton's ideas, and continued to apply Newton's ideas in wider fields than Newton had time to plough. Why did De Moivre link cos and sin as he did? Because Newton suggested it by his use of Bombelli's operator. Bombelli's tool or model vector was a set square, a right angled carpenters measure. Napier's tool was a huge Bombelli vector. Newton grasped the utility of the trig ratios in all sorts of measurement requirements, and conveyed that in his work. When Cotes began to converse with him, Newton came to realise he had someone capable of understanding his work. Newton opened up to him and De Moivre as he rarely did to any other. He told and showed them things we are only now becoming aware of in his scrapbook! In any case Cotes once again tackles the general solution for roots of polynomials and the problem of navigating the globe, in both cases he utilises the logarithmic series based on the sine as a starting point. De Moivre was there helping him and explaining how Bombellis vector worked as an analytical tool.  was De Moivres construction of a set square! He did not need to carry one physically, this odd aggregation structure actually did the trick. Meanwhile Cotes was able to demonstrate a neat solution to the latitude problem based on the logarithmic spiral, which he developed from Newton's influence and his own table of logarithms and differential identities based on the methods of fluxions, which as I have pointed out are applied trigonometry of moving objects. So it is hardly surprising that he comes up with  in his Logometrica with De Moivre around, because what this means is: take napiers method of making logarithms and apply it to the sphere and you will find the lines of longitude intersect a loxodromic spiral according to this rule. An equiangular spiral is what results. At the time these "numbers" were thought of as perfectly acceptable magnitudes, if properly distinguished and aggregated correctly. Descartes never understood them, nor did he want to but Bombelli made them "real" magnitudes to be learned and used. Newton did , and he taught De Moivre and Cotes to do the same. The three of them therefore had unusual success because they embraced these magnitudes readily. If De Moivre had not done so I doubt if Cotes would have come up with his logarithmic, loxodromic spiral equation a generation before Euler. Many are told Napier used base e for his logarithms, but he did not. However Cotes calculated his own logs using the logarithmic series Newton showed him, and he did use and calculate e a generation before Euler. Despite sounding complicated and looking long winded logs can be calculated for any number of geometric curved ratios, and it is indeed a marvel that the sine ratios can be put into such a sequence . It is even more amazing that they can be measured by a series! Geometrically though it is very easy to see how and what to do. Consequently Newtons discovery of the binomial series is a first result i think from his growing understanding of sequences and the applicability of logarithmic construction to solving curve compounding from tangents. Newton did not invent curve compounding, he simply saw further than his contemporaries the geometric construction for the compound interest curve and went from there. Many forget that calculus always has been a geometrical tool, and i can safely say that i was surprised to see it used in geometry when i first came upon it, because i was mis-taught its relevance to trigonometry. |
|
|
|
« Last Edit: November 12, 2011, 09:58:44 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #19 on: January 22, 2011, 02:16:43 PM » |
|
Anybody know when "imaginary" numbers became "complex" numbers and why?
I get the feeling that they are still a "dirty little secret" as far as maths goes.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #20 on: January 22, 2011, 09:11:30 PM » |
|
In order to remove them i must make clear the use of aggregate gate signs +(mod()) and disaggregate gate sign -(mod()). <Quoted Image Removed> cosin<Quoted Image Removed> for trigonometric sine scalars where  is an angle magnitude not an orientation. The aggregation structure for these scalars will be as expected Where the +(mod()) gate has not yet been determined but involvrs π/2 in some way, maybe as an angle magnitude. This seems strange , but it is more familiar as cos  + i sin  ! I So orientation does nothing!(Apart from distinguish that is, and that is very important and fundamental). To multiply different orientations is not possible. But to rotate to different orientations, and to multiply " via" different orientations does make sense 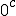 a* 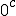 b= 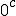 ab 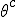 a* 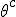 b= 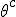 ab 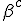 a* 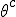 b =?. we could define it as 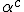 a*b*sin(  -  ) where 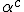 is perpendicular to 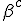 and 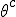 and  <  . The result is an area magnitude.  * 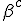 a=( 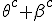 )a is a rotation by  radians anti clockwise along the circumference.  / 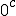 a=( 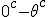 )a is a rotation by  radians clockwise along the circumference. The circumference for all these actions is along a great circle in a unit sphere. now ( 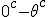 ) = ( 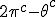 ) so in general  / 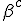 a=( 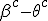 )a is a rotation by  radians clockwise along the circumference, but we have to take into account mod(2π) when writing the final orientation. Now for yoked pairs ( 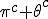 )a + ( 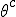 )b+( 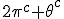 )c+( 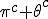 )d =( 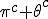 )(a-c)+( 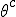 )(b-d) or ( 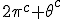 )(c-a)+( 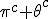 )(d-b) And for yoked triples ( 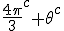 )a + (  )b+( 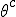 )c+( 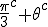 )d + (  )e+( 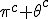 )f =( 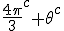 )(a-d)+ (  )(b-e)+ 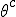 )(c-f) or ( 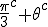 )(d-a)+ (  )(e-b)+ 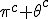 )(f-c) And yoked 4's for comparison ( 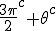 )a+(  )b + ( 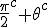 )c+( 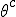 )d+( 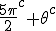 )e +( 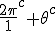 )f + ( 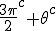 )g+( 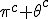 )h =( 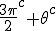 )(a-e)+(  )(b-f) + ( 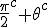 )(c-g)+( 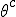 )(d-h) or ( 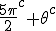 )(e-a) +( 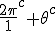 )(f-b) + ( 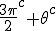 )(g-c)+( 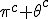 )(h-d) I have to admit, the notation is off putting in my view. Any suggestions? The c is starting to look like a power instead of a distinguisher. Now i would agree to calling these complex magnitudes!  The pattern is now being established for aggregation and the +(mod(rotate π)) or +(mod(2π)) aggregation gate is fundamental and clear. The fractal structure of the different yoked roots is also emerging, as i can further simplify in the roots which are 2 nth roots of unity, thus leading to compactness of notation. The flip algorithm is clearly in action and is fundamentally necessary. The relation to mod() arithmetics is there but not clear yet. And the operation of rotation is only partially explored. The logarithmic connection has not been addressed yet, and the relation to De Moivre's magnitudes only hinted at, and it is not clear yet if these behave like De Moivre magnitudes. So any one care to help? Bib maybe? All jump in whenever you like!  Just thought: relativity demands that I have an orientation measured relative to any surface as well as radially to a sphere. |
|
|
|
« Last Edit: January 26, 2011, 12:32:24 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #21 on: January 24, 2011, 11:52:28 AM » |
|
What do yo think to r for radial c for circumference measure placed before the greek symbol thusly 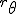 , 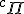 ? The radial is the orientation radial, and the circumference measure is an arc of a great circle on the surface of the unit sphere? |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #22 on: January 25, 2011, 04:03:21 AM » |
|
what would you like to know about roots of unity? the nth roots of unity can expressed as exp(iπj/n) = cos(πj/n) + i sin(πj/n) where 0 <= j < n from bethchen + i*sin(\frac{i*\pi*j}n)) Nice!  |
|
|
|
« Last Edit: January 26, 2011, 12:21:36 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #23 on: January 26, 2011, 12:33:14 AM » |
|
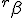 a* 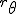 b =?. we could define it as 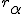 a*b*sin( 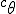 - 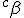 ) where 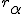 is perpendicular to 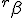 and 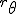 and 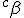 < 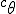 . The result is an area magnitude. 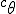 * 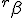 a=( 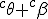 )a is a rotation by 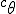 radians anti clockwise along the circumference. 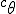 / 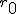 a= r( 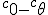 )a is a rotation by  radians clockwise along the circumference. The circumference for all these actions is along a great circle in a unit sphere. now r( 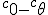 ) = r(  ) so in general 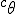 / 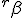 a= r( 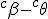 )a is a rotation by  radians clockwise along the circumference, but we have to take into account mod(2π) when writing the final orientation. Now this is getting somewhere. But i have to be very careful because i am using 2 magnitudes now not directions "suggesting" appropriate magnitudes. 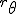 is a unit magnitude direction distinguisher assigned or attributed to only one radial on a unit great circle. is a unit magnitude direction distinguisher assigned or attributed to only one radial on a unit great circle. 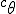 is a magnitude of a part of the unit great circle circumference . Now it is assigned a direction relative to rotating around a perpendicular or orthogonal axis, orthogonal to every one of the radii in the circle. is a magnitude of a part of the unit great circle circumference . Now it is assigned a direction relative to rotating around a perpendicular or orthogonal axis, orthogonal to every one of the radii in the circle.So i also have another constraint on the 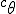 , and that is a great circle rotation direction. I could use 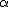 for anticlockwise and c for clockwise rotation. The relations above then become: 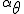 * 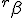 a= r( 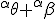 )a is a rotation by  radians anti clockwise along the circumference of a great circle. now r( 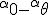 ) = r(  )= r( 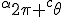 ) and i see here the familiar Bombelli operator --=+, in this case written as disaggregating a clockwise rotation is the same as aggregating an anticlockwise rotation. This is written so formally to convince you that the distinctions i am trying to make have a real sense that is symbolically the same as the traditional Bombelli operator. so in general 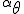 / 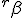 a= r( 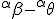 )a is a rotation by  radians clockwise along the circumference, but we have to take into account mod(2π) when writing the final orientation. This is strange, but for now i will just say it is a definition. |
|
|
|
« Last Edit: January 26, 2011, 08:18:02 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #24 on: January 26, 2011, 09:14:45 AM » |
|
I know i am close because i woke with this : }{^r\frac\pi 21(sin(^\alpha\frac \pi2-^\alpha\theta))}^n) Which is complicated to write, especially in latex, but is geometrically straightforward, and it is based on these discussions (so far with myself!- any body out there want to help?) and the method Napier used to construct his logarithms. How can i get to Cotes formula from here? What constraints or definitions do i need to make this work consistently? Here is some blue skying i did earlier which might help. Help, anyone?  |
|
|
|
« Last Edit: January 26, 2011, 07:51:01 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #25 on: January 26, 2011, 08:57:01 PM » |
|
I made a mistake of sorts, but it is very revealing. )^n) means that the result of finding the sin value is oriented to the rπ/2 radial of the great unit circle. However the calculation depends on a right angled triangle, and every line in the triangle has an orientation. The orientation radial of the hypotenuse is required to calculate the magnitude of the opposite side of a right angled triangle, That is what i forgot o=rsinø so this part of the procedure should read 1*sin(^\alpha\frac \pi2-^\alpha\theta))^n) = )^n) These are expressions to be read not rushed. When read steadily they enable one to construct a geometrical figure which represents the action of the procedure. it is becoming apparent that these are algorithms controlling or describing the dynamic transformations of these magnitudesThese dynamic magnitudes have 3 descriptors of dynamism: orientation radial,rotation radian magnitude, and spatial magnitude. These are consequently more complex to deal with, but also more rewarding, as you feel the transformations are occurring before your eyes and at your request. The corrected algorithm is : }{(^r(\frac \pi2-\theta)1*sin(^\alpha\frac \pi2-^\alpha\theta))}^n) This makes perfect sense as a logarithm table, so why is 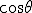 included in DeMoivre and Cotes? |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #26 on: January 26, 2011, 10:39:50 PM » |
|
The answer to my question is going to be found here. Anybody seen this before? In fact the answer is with Newton and Wallis as i once surmised, Wallis himself being the source of so many of Newtons ideas And here it is Newtons spherical trigonometry the same which or a progenitor of which inspired De Moivre and Cotes De Moivre was following Newton in using trig functions to solve quadratic and higher equations. It is clear from my investigation that both Cotes and De Moivre were privy to papers and idead from Newton that others never heard or saw. Newton himself was inspired by Wallisa and schoeten in the acceptance of complex numbers, but i think it was De Moivre who actually combined the trig and complex in the style of Newton to solve equations Newton did not have time to. Similarly Cotes applied Newton's logarithm algebra to solving harmonic means and ventured into spherical trig logarithms, using his own differential identities and logarithmic tables he constructed himself in the style of Newton, It was De moivre who in 1707 came across a version of 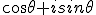 and informed Halley and cotes of solutions he had obtained relevant to their search for a longitude convention to augment the navigational spherical trig, So i need to look more carefully at the properties of these notations to see if i have missed something else in relation to solving polynomial equations of arbitrary degree |
|
|
|
« Last Edit: January 27, 2011, 02:47:53 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #27 on: January 27, 2011, 08:45:59 AM » |
|
The thing i missed is Viete's Law of Cosines.. There is no doubt that Wallis and Newton knew it and employed it in calculating the compounding of the tangents to an orbit. De Moivre Took it to its Ultimate Conclusion. Wallis had already revolutinised Conics, by using a Cartesian approach, and through his formula for the circle, guessed that certain polynomials/multinomials whose equations could be classified as describing points on a circle in the x,y plane would have solutions involving imaginary magnitudes. It lead him to conjecture that imaginary magnitudes had a representation on the plane! He saw that it would apply to all closed conic curves and venttured to explore parabolic and hyperbolic in these terms. He trumpeted the algebraic Geometry over the use of cones and planes, that is over the use of carpenters models created by rotation and slicing. Therefore he trumpeted his algebraic tools over the carpenters tools. He investigated calculus before Newton, but was only able to lay the groundwork for Newton to take it further, as he hoped. Newton of course did so, and immediately applied it to solving equations of the nth degree in cartesian form, and thus discovered polar elliptical and other coordinate systems, a generalised coordinate measure, inspired by Wallis's work, in 1686 onwards while at his family farm. Newton put these notions to one side to concentrate on his fluxions! De Moivre then had a rich background to draw on, including Walis's groundbreaking work in trigonometry both spherical and planar, and a loyal if not tentative tutor in Newton. He also came into tje orbit of the brilliant Cotes who shining like a star next to Newton was in his ascendancy before his sudden death. The two collaborated very closely it would seem, sharing results and notions to each others mutual benefit. Meanwhile, Wallis kept a wary eye on the continental mathematicians in case they stole a march on Newton and his Ideas. It was Newton's tardiness to publish that lead to the controversy with Leibniz, and the man who knows the truth of the collaboration between english and continental mathematicians was Wallis, and he knew how easily continental mathematicians plagiarised others work without acknowledgement! The political times were those of the puritans for whom uprightness of moral character was fundamental. Thus to claim a lesser's work because one was of nobler birth was morally reprehensible to Wallis, and politically fraught with implication. Cromwell had deposed the king for moral Corruption. |
|
|
|
« Last Edit: January 28, 2011, 02:46:28 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #28 on: January 29, 2011, 07:29:29 AM » |
|
Actually the thing i missed is polynomial factorization. It is not surprising really with everyone shouting"roots of unity" I actually have to start with acceptance of i as a "number" which it is not, it is an oriented magnitude with a bombelli operator controlling the orientation and thus the aggregation structure and summation. The orientation is assigned by a flip condition and the intention and construction of the measurer, and only dynamic systems flip or are motile, thus i is part of a dynamic measuring system and concept. So as a "number" i would expect factorsor ratios, and this is where D Moivre started: he wanted to discover the unit of these complex, or imaginary numbers and familiarise himself with the way they added subtracted, multiplied and sivided and formed factors: in short how they behaved as numbers or magnitudes. In De Moivres day number , magnitude, quantity arithmoi all meant the same thing essentially, just in the different languages that were used for scholarly communication. It was virgin territory and his investigations would overturn the concept of number down to this day. However human animates are a sentimental breed and they have clung to the concept number, even defining it so rigorously that they excluded imaginary magnitudes. They were only accepted because there was nothing else they could do, and they enriched the idea of number in odd and curious ways,by deining abstract objects like rings groups and fields,and sets in order to try to cope with the burgeoning and incredible outfall from these" complex "number" calculations and observations. People worked with complex numbers with trepidation, because their natural tendency was toward the infinite sum of infinite series, and infinite sequences of factors! This is what De moivre Noticed from the unit circle work Newton did Therefore De Moivre took 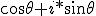 as the first factor of unity and 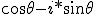 as the second factor It was immediately clear that there were infinitely many factors of unity,but they were yoked in conjugate pairs. These conjugate pairs were always oriented 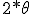 radians to each other . The question then becomes is the 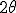 seperation significant, or just a fluke? are all complex factors of unity 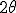 apart indeed factors of unity? Do they need to be 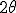 apart? These investigations naturally lead to the roots of unity theorem, and the dynamic flip rotation around the circle. |
|
|
|
« Last Edit: November 12, 2011, 10:25:38 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #29 on: January 29, 2011, 09:38:50 AM » |
|
Number theory.. I have found some papers of the late (very late!  ) Mr. Henry John Stephen smith, Some presented to the london mathematical society in around 1880+ which deal very fully with this topic of complex factors of unity and much else besides, in fact is life's work, with biographical sketch. I dare say that had De Moivre, Euler and Gauss not had the preeminency that these would have obtained a wider fame. Nevertheless they show in great detail the extent of number theory and algebra at the time of William Hamilton, and the use of modular arithmetic notation, as in Kujonai, and the continuing doubt of mathematicians in the usefulness of these considerations even at that time. I think Mr Smith,Krummer, et al have demonstrated that " numbers" are not based on natural counting numbers at all, nor on a Number line concept, but rather firmly and incomprehensibly if you believe in numbers on imaginary or complex numbers of a polynomial form, which exhibit modular behaviour. Now, unless Russel And A.N, Whitehead have stated and proved in symbolic logic the same thing, their work is in need of a slight revision. AS i do not believe in "numbers" so called, that is following Dedekind et al, i have no problem in accepting the trigonometric relations that underlie all or conception of magnitude, to which Wallis, Newton, Cotes, Napier,Bombelli, Brahmagupta have so ably contributed their insights and which Wessel, Euler, Gauss, Bernoulli Leibniz have Given some groundbreaking exposition.
Therefore Mr.Smith's, Krummer's,et al Labours, and Sir William Hamilton's have such eminent predecessors on which to draw, that it is hardly surprising that they made such advances in the complex magnitude basis of our measurement system. This just makes a meal out of some dry bones! Vectors developed under the whip hand of Hamilton, although Moebius and Grassman, and Rodrigues had similar pursuits and concerns. The reason behind this push is that we measure in 3d, and we compare and contrast in 3d, and we distinguish in 3d. A "one or 2 dimensional number system" is not enough! We actually require an n dimensional magnitude measuring system! We have one now, called a tensor system. More obfuscation, and mystifying of what Artists and artisans, Musiscians and Dancers Do everyday! We all measure as an act of existence! "I sense therefore i am", kind of thing. What we do is undoubtedly convoluted and iterative, and therefore to write it down is like unraveling a ball of wool! Better to apprentice a student and show and guide him/her in play mode than to task them to read overmuch! Dirac, when he started Quantum mechanics Made certain he had a good grasp of what we do when we measure, developing what looks like a vector math, but was in fact his measuring tool! It comes down to being real simple: i am a measuring tool: 'man is the measure is the measure of all things". I devise measuring tools and the algorithms that are needed to operate them, thus i choose and decide ad observe and promulgate certain activities. These i iterate, or observe to be iterating by establishing certain flip algorithms, which control my subsequent aggregation of my iteratively produced data. My tool enables me to create data, calculate data and display data in various formats, and verify the accuracy of my calculated outputs by test measurements. What? This souns like a computer? Too right! The universal machine as Turing imagined it was always going to be able to mimic human ability. As such it becomes mans ultimate measurement system. It hard to not see the inevitability of computer systems arising as tools of measurement, but it is nevertheless a startling and stunning achievement which highlights for me a fundamental fractal convolution(truth?): the computation will iterate and produce fractals! "Its all greek to me", " Its all based on 0 and 1"," It is only addition, subtraction and counting" all are aspects of this dynamic magnitude measurement system we are experiencing and playing with, artistically.
|
|
|
|
« Last Edit: January 30, 2011, 11:12:14 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|










