Hi,
In principle, one could adress the accuracy problem by using interval/affine arithmetics methods. one of these metods can be defined as:
[z] = z + dz*t + 1/2 ddz*t² + ... + R*|t
n+1|*E
Where dz is the first derivative of z, ddz the second derivative ...etc.
R*|t
n+1| is a positive real number giving the error in the O(t
n+1) term.
E is the unit disc centered at 0. E = [0,1]*exp(i*]-infinity, +infinity[
In the case of the series approximation we have:
Z
n = z
n + a
1,n*t + a
2,n*t
2 + ... + a
m,n*t
mOne can verify that the a
i,n are equal to d
(i)z
n/i! for all i<m . for i==m it is slightly different.
Let's write Z
n in interval form (for m=3 for simplicity):
[Z
n] = z
n + a
1,n*t + a
2,n*t
2 + a
3,n*t
3 + R
n*|t
4|*E
Or using the notation in the original superfractalting paper:
[Z
n] = z
n + A
n*t + B
n*t
2 + C
n*t
3 + R
n*|t
4|*E
We have
[Z
n+1] = [Z
n]
2 + [Z
0]
(... some algebra manipulation ...)
[Z
n+1] = z
n+1 + A
n+1*t + B
n+1*t
2 + C
n+1*t
3 + R
n+1*|t
4|*E
Where (hopefully):
A
n+1 = 2*z
n*A
n + 1
B
n+1 = 2*z
n*B
n + A
n2C
n+1 = 2*( z
n*C
n + A
n*B
n)
And:
R
n+1 = B
n2 + 2*(|z
n|*R
n + |A
n|*|C
n|) + 2*|tmax|*(|A
n|*R
n + |B
n|*|C
n|) + |tmax
2|*(|C
n|
2 + 2*|B
n|*R
n) + 2*|tmax
3|*|C
n|*R
n + |tmax
4|*R
n2Where |tmax| is the maximal distance between the reference point and the corner points.
I use "reduction" operations to obtain R
n+1. The rules are:
- Replace any complex number by it's absolute value.
- Replace |t
k| by |t
m+1|*|tmax
k-m-1| whenever k>m+1. (in our case m=3)
- Remove any occurence of E in the computation of R
n+1. It is added afterward.
(Remark: Obviously,
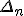
is obtained by removing the z
n and error terms from [Z
n])
Ok! the formula for R
n+1 is lengthy: it requires m+2 terms. Moreover, it also requires absolute values => square roots... but:
- Some of the terms are very small and could be skipped safely.
- Using disk interval (which requires the absolute value) prevents excessive (actually catastrophic) growth of it's size. For example multiplying a disk interval by
)
doesn't change it's size but a sqare interval's size will be multiplied by
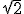
.
- The computations are done once for each reference point. Moreover they can be done in parallel with the computations in full accuracy of z
n.
Another drawback of (all?) interval arithmetic methods is that it is very conservative: at some point the error term grows extremly fast.
We are not finished yet

! The question is how to use it?
Say, we have a function y(x). For some small enougth
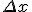
we have:
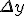
= y' *
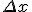
Let us call
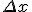
and
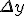
absolute
errors variations. Their absolute values will be called the errors.
The question that we are asking is: What is the maximal allowed error on y that corresponds to some allowed error on x?
In other words :
|
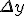
| <= |y'|* |
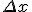
|
Here |
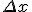
| will be some fraction of the size of the area corresponding to a pixel. It depends on the resolution and the zoom factor.
y will correspond to
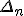
and y' to the derivative of
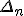
(Wich is: A
n + 2*B
n*t + 3*C
n*t
2)
|
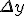
| is simply given by R
nTherefore, the accuracy of the series approximation is sufficient if the following condition is met:
R
n <=
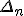
'* |
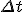
|
___________________________________________________________________________________
For the detection of the glitches caused by the numerical inaccuraces, a similar approach can be used: The question is:
What is the maximal allowed
relative error on y that corresponds to some allowed
absolute error on x?
That is, if:
|
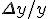
| > |y'/y|* |
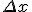
|
is true then the accuracy is insufficient and a glitch occures.
y is replaced by :
 \delta_{n} + \delta_{0})
y' is replaced by :
 \delta_{n}' + 1)
|
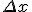
| will be some fraction of the size of the area corresponding to a pixel. It depends on the resolution and the zoom factor (replaced by
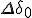
).
|
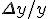
| is replaced by the relative accuracy in the computation of
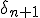
. Ignoring the accumulation of rounding errors and taking into account only the cancellation that may occure in the computation of
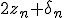
, I get:
|
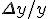
| = max(2|z
n|,|
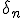
|)/|
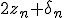
| * 2
-pmaxpmax is the number of bits in the mantissa.
So the glitch condition becomes:
 |\delta_{n+1}|> |2 z_n + \delta_n| |\delta_{n+1}'| |\Delta \delta_{0}| )
I was hoping to obtain something as simple and effective as Pauldelbrot's formula

. Nevertheless, it's in fact quite close... Why?
The formula above tells us that a glitch may occure if: the floating point type used is not accurate enougth, the derivative of
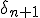
is too small and/or if |
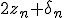
| is also too small w.r.t. |z_n| or
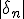
. It also says there will likely be more glitches at higher resolutions.
For deep enough a zoom, adding
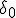
is irrelevant (as Pauldelbrot noticed) and corresponds to a null operation. In this case, the derivative of
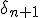
shouldn't include the +1 and becomes
 \delta_{n}')
Ok! This post is becoming too long. I doubt all the above formulas have any practical use at least because they require a lot of computations. In case I didn't do too big mistakes it shows that it is possible to quatify the approximation and accuracy errors.
___________________________________________________________________________________
PS:
The relation between the relative variations
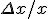
and
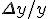
is :
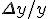
= x*y'/y *
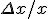
Here
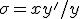
is the
condition "number" of y.


















