quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #195 on: August 12, 2016, 02:12:49 PM » |
|
the code is available, and yes most of it is written in assembly to try to achieve as much performance as possible. though some drawbacks to that are being buggy, unmaintainable, and nonportable.
in any case, i only mentioned it to point out that some of these algorithms may not be as perfect as they maybe could be, and to encourage any intelligent and honest conversation that might be had here with regard to our understanding of them and what further progress might be made.
|
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #196 on: August 12, 2016, 11:38:03 PM » |
|
since nobody else seems interested, i guess i'll try implementing knighty's wall of math and report back with any success stories, though i dont know if i will be able to decipher it. it would be neat if you guys could dumb it down once in a while for us non-math folk.  for instance, i dont know what R 0 should be. i dont know what E is. i dont know what this means: "E = [0,1]*exp(i*]-infinity, +infinity[". and im not sure how all this is supposed to be used either. is this intended for the checking against arbitrary points to determine the number of iterations to then skip for all points in the image, like how people have been doing? or is this R thing supposed to be used during the initialization of each point, where if an error tolerance is exceeded you just try that point again later with another reference point? That would be great! E is an error symbol. "E = [0,1]*exp(i*]-infinity, +infinity[" is just a way to say "E is the unit disc centered at 0". One doesn't need to worry about it when writing the code. The only formula needed is: R n+1 = |B n| 2 + 2*(|z n|*R n + |A n|*|C n|) + 2*|tmax|*(|A n|*R n + |B n|*|C n|) + |tmax 2|*(|C n| 2 + 2*|B n|*R n) + 2*|tmax 3|*|C n|*R n + |tmax 4|*R n2R n+1*|tmax| 4 is the radius of the disc interval. It is the maximal error that we do by neglecting the higher order terms of the series approximation ( truncation error). R 0 = 0. Simply because there is no truncation error. It remaines equal to zero until the third iteration (or so  ) The question that we are asking is: What is the maximal allowed error on y that corresponds to some allowed error on x?
In other words :
|Deltay| <= |y'|* |Deltax|
Here |Deltax| will be some fraction of the size of the area corresponding to a pixel. It depends on the resolution and the zoom factor.
y will correspond to Delta_n and y' to the derivative of Delta_n (Wich is: An + 2*Bn*t + 3*Cn*t2)
|Deltay| is simply given by Rn
Therefore, the accuracy of the series approximation is sufficient if the following condition is met:
Rn <= Delta_n'* |Deltat|
I did some mistakes here. Good news: It should be: R n*|tmax| 4 <= | 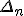 '|* | 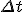 | Because the trucation error is R n*|tmax| 4 not R n. As it is that formula have to be computed for each pixel because 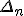 '=A n + 2*B n*t + 3*C n*t 2is function of t. But we are interested in its minimal absolute value among all the values of t spanning the zoomed area. A lower bound can be computed using interval arthmetics. I'll come back tomorrow after doing the compuations and checking them.  PS: For deep enought zooms, the bottelneck is mainly in the computation of the references. It is possible to avoid unnecessary computations by reusing the reference until glitches occure. For example, if the reference is centered on the root of a minibrot, one can still use that same reference when zooming near that minibrot. It is also possible to refine a refrence using perturbation (+ Newton). |
|
|
|
« Last Edit: August 13, 2016, 10:19:02 PM by knighty »
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #197 on: August 13, 2016, 10:37:12 PM » |
|
Ok! The last formula for cheking if the series appriximation is good at iteration n should be: R n*|tmax| 4 <= (|A n| - 2*|B n|*|tmax| - 3*|C n|*|tmax| 2)* | 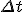 | Where: R n*|tmax| 4 is an upper bound on the truncation error. (|A n| - 2*|B n|*|tmax| - 3*|C n|*|tmax| 2) is a lower bound on the absolute value of the derivative. As it is, it can be negative which means that the derivative could be 0 somewhere so the approximation's quality is likely to be too low. | 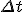 | is related to the "radius" that corresponds to a pixel. |tmax| is the maximal distance between the reference point and any point of the rendered area. |
|
|
|
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #198 on: August 14, 2016, 12:25:20 AM » |
|
cool, thanks for your work on this! i'll [try to] check it out  for extrapolating your formulas to an arbitrary number of terms, i see the pattern here: R n*|tmax| 4 <= (|A n| - 2*|B n|*|tmax| - 3*|C n|*|tmax| 2)* | 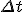 | but this one im not sure: R n+1 = |B n| 2 + 2*(|z n|*R n + |A n|*|C n|) + 2*|tmax|*(|A n|*R n + |B n|*|C n|) + |tmax 2|*(|C n| 2 + 2*|B n|*R n) + 2*|tmax 3|*|C n|*R n + |tmax 4|*R n2maybe i just need to look at it longer |
|
|
|
« Last Edit: August 14, 2016, 05:25:53 AM by quaz0r »
|
 Logged
Logged
|
|
|
|
|
Kalles Fraktaler
|
 |
« Reply #199 on: August 14, 2016, 10:50:31 AM » |
|
A, B and C are 3 terms, but KF, and MM are using arbitrary many terms.
And therefore we can render magnum opus thousands or ten-thousands times faster than FX...
|
|
|
|
|
 Logged
Logged
|
|
|
|
stardust4ever
Fractal Bachius

Posts: 513
|
 |
« Reply #200 on: August 14, 2016, 11:02:59 AM » |
|
A, B and C are 3 terms, but KF, and MM are using arbitrary many terms.
And therefore we can render magnum opus thousands or ten-thousands times faster than FX...
hehe...  |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #201 on: August 14, 2016, 03:01:12 PM » |
|
One can get the formula of R for any number of terms in the series approximation.
The formula is given for a 3-terms only for simplicity and in order to test the idea.
|
|
|
|
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #202 on: August 16, 2016, 03:46:01 AM » |
|
   it works, and it works WELL! it is taking me farther than the old method of checking when the last term grows larger than the others by a certain amount yada yada, and is even skipping a few more than my experiment with using series acceleration error as the check (which itself was better than the other thing)! and everything rendering fine as far as i can tell so far. awesome!   noting though that my program is currently setup to use a minimum of 8 terms, so hopefully it still bails soon enough when using the same number of terms. also i wasnt sure what 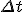 is supposed to be, so i made it the distance between adjacent points.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Pauldelbrot
|
 |
« Reply #203 on: August 16, 2016, 04:20:36 AM » |
|
Do you have (pseudo) code? |
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #204 on: August 16, 2016, 05:11:26 AM » |
|
cool, thanks for your work on this! i'll [try to] check it out  for extrapolating your formulas to an arbitrary number of terms, i see the pattern here: R n*|tmax| 4 <= (|A n| - 2*|B n|*|tmax| - 3*|C n|*|tmax| 2)* |<Quoted Image Removed>| but this one im not sure: R n+1 = |A n| 2 + 2*|z n|*R n + 2*|tmax|*|A n|*R n + |tmax 2| * R n2m = 2R n+1 = 2*|z n|*R n +2*|A n|*|B n| + |tmax|*(2*|A n|*|R n|+|B n| 2) + |tmax 2|*2*|B n|*R n + |tmax 3|*R n2m = 3 (from above quote) R n+1 = |B n| 2 + 2*(|z n|*R n + |A n|*|C n|) + 2*|tmax|*(|A n|*R n + |B n|*|C n|) + |tmax 2|*(|C n| 2 + 2*|B n|*R n) + 2*|tmax 3|*|C n|*R n + |tmax 4|*R n2maybe i just need to look at it longer
trying the same here  mostly on paper doing boring algebra to get a feel for how it works (results above for m=1,2) writing with indices helps, addition of letters is awkward - something like  (omitting the n that occurs everywhere seems to make sense too for this part of the algebra scribbling on paper) cool stuff knighty! UPDATEUsing the notation from my blog post, https://mathr.co.uk/blog/2016-03-06_simpler_series_approximation.htmlRecall the coefficients are   Use 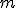 "  " terms, so the coefficient of the truncated part starting  is  (using hat for disc interval), and writing T for tmax, and aliasing  and  , I think it boils down to this: 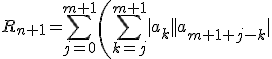 |T|^{j} ) note this includes some terms twice multiplied in opposite orders, could be implemented by multiplying by 2 instead of repeated calculations |
|
|
|
« Last Edit: August 16, 2016, 05:40:41 AM by claude »
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #205 on: August 16, 2016, 05:43:28 AM » |
|
Do you have (pseudo) code? truncError = 0; series approx loop { calculate_series_coefficients(A, B, C); truncError = |B| 2 + 2*(|z|*truncError + |A|*|C|) + 2*|tmax|*(|A|*truncError + |B|*|C|) + |tmax 2|*(|C| 2 + 2*|B|*truncError) + 2*|tmax 3|*|C|*truncError + |tmax 4|*truncError 2; if ((truncError * |tmax| 4) > ((|A| - 2*|B|*|tmax| - 3*|C|*|tmax| 2) * | 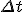 |)) { // this is the iteration i'll initialize all other points at anything_else_you_do_when_you_bail_on_series_approx(); } } i just kinda copy pasted what was already here, maybe that doesnt help much  z is the reference Z ntmax i just set to the sidelength of the image for simplicity 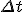 i set to the distance between points im not sure if thats all right but thats what i did just now and it seems to work. update: continued testing the last hour or two with no problems. manual zooming for a while and also tested an ultradeep location. |
|
|
|
« Last Edit: August 16, 2016, 06:42:11 AM by quaz0r »
|
 Logged
Logged
|
|
|
|
|
Pauldelbrot
|
 |
« Reply #206 on: August 16, 2016, 07:18:09 AM » |
|
truncError = 0; series approx loop { calculate_series_coefficients(A, B, C); truncError = |B| 2 + 2*(|z|*truncError + |A|*|C|) + 2*|tmax|*(|A|*truncError + |B|*|C|) + |tmax 2|*(|C| 2 + 2*|B|*truncError) + 2*|tmax 3|*|C|*truncError + |tmax 4|*truncError 2; if ((truncError * |tmax| 4) > ((|A| - 2*|B|*|tmax| - 3*|C|*|tmax| 2) * |<Quoted Image Removed>|)) { // this is the iteration i'll initialize all other points at anything_else_you_do_when_you_bail_on_series_approx(); } } i just kinda copy pasted what was already here, maybe that doesnt help much  z is the reference Z ntmax i just set to the sidelength of the image for simplicity <Quoted Image Removed> i set to the distance between points im not sure if thats all right but thats what i did just now and it seems to work. update: continued testing the last hour or two with no problems. manual zooming for a while and also tested an ultradeep location. Thanks. This looks like it's for just three terms though... |
|
|
|
|
 Logged
Logged
|
|
|
|
quaz0r
Fractal Molossus
 
Posts: 652
|
 |
« Reply #207 on: August 16, 2016, 07:34:33 AM » |
|
This looks like it's for just three terms though indeed, you guys are the mathematicians, i await your brilliance to shed further light on the matter..  it looks like claude may have posted a formula for arbitrary number of terms there, though i have a hard time decoding that math stuff |
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #208 on: August 16, 2016, 11:52:08 AM » |
|
Rn+1 = |Bn|2 + 2*(|zn|*Rn + |An|*|Cn|) + 2*|tmax|*(|An|*Rn + |Bn|*|Cn|) + |tmax2|*(|Cn|2 + 2*|Bn|*Rn) + 2*|tmax3|*|Cn|*Rn + |tmax4|*Rn2
Rn+1*|tmax|4 is the radius of the disc interval. It is the maximal error that we do by neglecting the higher order terms of the series approximation
Hm, with R n depending on |tmax| like that, it makes it harder to cache the series approximation coefficients when zooming around a still-good primary reference... Running some tests with order m=16 now, seems promising so far it skips at most 1 period of the reference? while other skipping methods allow skipping beyond that. (I got rid of the off-by-one bugs elsewhere in the code). Demonstration-quality C++ code attached, note that it detects glitches but doesn't correct them, and location is hard-coded with a zoom sequence. I plan on updating it with glitch correction and exterior distance estimation once I get the truncation error stuff for the derivative's series approximation sorted. Equation scribbling ahoy... |
|
|
« Last Edit: August 16, 2016, 12:22:38 PM by claude, Reason: skipping 1 period only? »
|
 Logged
Logged
|
|
|
|
|
Kalles Fraktaler
|
 |
« Reply #209 on: August 16, 2016, 02:07:31 PM » |
|
truncError = 0; series approx loop { calculate_series_coefficients(A, B, C); truncError = |B| 2 + 2*(|z|*truncError + |A|*|C|) + 2*|tmax|*(|A|*truncError + |B|*|C|) + |tmax 2|*(|C| 2 + 2*|B|*truncError) + 2*|tmax 3|*|C|*truncError + |tmax 4|*truncError 2; if ((truncError * |tmax| 4) > ((|A| - 2*|B|*|tmax| - 3*|C|*|tmax| 2) * |<Quoted Image Removed>|)) { // this is the iteration i'll initialize all other points at anything_else_you_do_when_you_bail_on_series_approx(); } } i just kinda copy pasted what was already here, maybe that doesnt help much  z is the reference Z ntmax i just set to the sidelength of the image for simplicity <Quoted Image Removed> i set to the distance between points im not sure if thats all right but thats what i did just now and it seems to work. update: continued testing the last hour or two with no problems. manual zooming for a while and also tested an ultradeep location. Seems tmax and 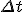 are limited to double precision, unless you are using some other datatype? |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















