END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

The Mandelbox is a year old today  
I hope people don't mind me referencing their work, thanks ...

Inspired by Daniel White's Mandelbulb and later by msltoe's fractals, and using David Makin's UltraFractal code, I started it here:
http://www.fractalforums.com/3d-fractal-generation/amazing-fractal/
Here's the first picture, using scale=3:

We soon realised that scale 2 was less separated, this picture was in Bib's exhibition and made only 3 days after first discovery:

Here's another scale 2:

The scale 2 also became a competition winner with this classic by Jesse, still the top rated:


The first deviation was to try negative scales, this, also by Jesse, really showed what the Mandelbox could do-

DeviantArt got involved too, here's an example of the -1.7 structures, by MarkJayBee:

Buddhi made a movie of a scale -1.7 which now has almost 300,000 views and is so prominent that it is the first movie if you google search '3d fractal'!
<a href="http://www.youtube.com/v/bO9ugnn8DbE&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/bO9ugnn8DbE&rel=1&fs=1&hd=1</a>
Vegetation was also discovered around this time!


The next deviation was negative scales close to -1 with 0 minRadius, e.g. this by Jesse:

We also began to see all the different fractals that these Mandelboxes mimic:
http://www.miqel.com/fractals_math_patterns/mandelbox_3d_fractal.html
https://sites.google.com/site/mandelbox/negative-mandelbox
https://sites.google.com/site/mandelbox/more-negatives

Sometime later Trafassel had the ingenious idea of looking at these -ve scale mandelboxes from the inside. So solid becomes space and space becomes solid:
http://www.fractalforums.com/3d-fractal-generation/inner-view-of-the-mandelbox/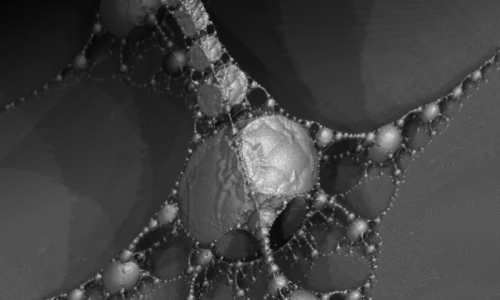


Shortly after it was discovered that applying a small rotation in the iteration turned the mandelbox images into something even more organic,
e.g. this by Mandelwerk:


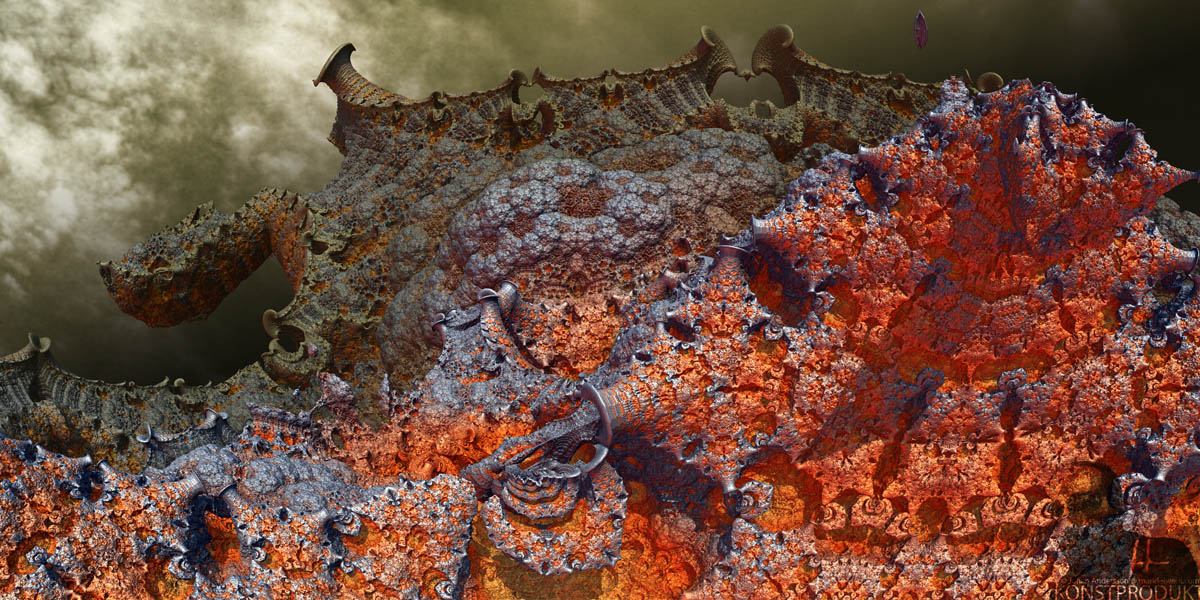
The deviations have magnified since then, there are flips and sines and int power things that I don't even know how they work, but they are producing amazing images
Like this by fractal00:

And this by pixelcomposer:

The list of great images goes on...

and on...


So thanks to Jesse and Buddhi and David for making the software that lets us explore, and all the artists for their inspiring work, here's to a year of 3d fractal wonder!  

I'll finish with a partial attempt at explaining why the Mandelbox mimics so many other fractals...
Most fractals are generated by repeated translation, rotation and scale. This is why the kaleidoscopics cover such a wide range of different fractal shapes, they can be sierpinski pyramids, menger sponges, trees and almost any simple fractal in between.
The Mandelbox only uses one formula per image, but the sphere invert is crucial. A fold around one of the box sides followed by the sphere inversion is, for any small shape, equivalent to a rotation + scale, since two reflections give a rotation. This means that at different locations in space the Mandelbox folds result in different rotations, and different scalings (a point near 0,0,0 will give a bigger scaling than a farther point). The +C part of the formula ensures different translations. So the Mandelbox is acting like a different kaleidoscopic at each point in space, e.g. when it acts like the manger sponge kaleidoscopic, that part of the image will look like a menger sponge.

Yea - Happy Birthday to the Box !

I'm determined to eventually make time to put together full escape-time RIFS (and procedural trees etc.), 'bulbs, 'boxes and KIFS and anything else I can think of in such a way that they're as controllable as (or more controllable than) 3D+ L-Systems.
Plus re-code things where possible so that individual sections of the fractal objects can be "broken off" from the whole to be treated as separate objects - in a reasonably controllable manner of course e.g. from within a given blast radius

Happy birthday to our beloved box

Iterated thanks to you Tom for the formula of the year 2010, and I'm sure far beyond...

And thanks for showcasing one of my early images, you are "the Genius" on the small list of people that were on the critical path to the success of my exhibition, like Dave (the Guru), Christian (the Boss), Jesse (the Master), Jos (the Advisor), Tim (the mad blogger), of course Daniel and Paul (the Prophets), plus all my parisian contacts in the "real" world of course who made it physically possible.



Isn't that simply a julia of the local area?

well well, happy birthaday as well from me,
the box is for sure the most amazing find last year, and the fact that nowadays fractal renderer easily combine existing formulas is a beauty!
without the mandelbulb there wherent such raycasting renderers to easily check out new formulas
 

All amazement is down to the fantastic artists here and on deviantArt.
Bib, you should be "the artist", since having a real exhibition gives you that title.
 

Happy birthday to the mbox!

Tglad, wonderful images in this thread, some I hadn't seen before. Congrats all round.

I'd love to do an article and story about the Mandelbox sometime, but that would be one heck of a task because of the incredible variety, and obviously, there are still new surprises cropping up to today.

I've started work on a new raytracer (with GUI this time), and I can't wait to explore the Mandelbox and other objects with it.