Earlier this year I was exploring inversive geometry and implementing some new ideas as "variations" for IFS in JWildfire. I ended up writing a paper summarizing some of that work/play:
Inversive Diversions and Diversive Inversions. And I'm giving a talk on it at the Bridges Math/Art conference later this week!
Now I'm experimenting with applying similar ideas to escape-time fractals. Which led me to implementing Mandelbox modifications in Fragmentarium. Well actually I've started with a 2D version of the Mandelbox, as I wanted to start simple.
The images and code below are my first attempt at modifying the circle inversions in the 2D Mandelbox to use a more generalized shape inversion. The idea is that the geometry to calculate inversion only requires determining two distances:
d(
OP), the distance from the origin
O of the inversion to the point
P being inverted (transformed to
P' d(
OS), the distance from
O to the unique point
S on the boundary of inversion that lies on the line segment
OPInversion is then:
P' =
P * [d(
OS)]^2 / [d(
OP)]^2
In the case of a circle, d(
OS) is a constant: the radius of the circle of inversion. But the same equation can be applied to non-circular shapes as long as there is a way to determine d(
OS), given
O and
P. Shapes that have a polar coordinate parameterization are good candidates to use for 2D shape inversion, as finding d(
OS) can be done by calculating the polar angle of
P relative to origin
O, then plugging this back into the polar parametric equation to get the radial distance of the parameterized shape at the given angle, which is d(
OS). The same reasoning applies to generalizing sphere inversion to 3D shape inversion. And shapes that have a spherical coordinate parameterization are good candidates to use for 3D shape inversion via a similar strategy. For more details and examples see the
paper mentioned above. And for much more detail check out the references my paper cites -- I'm largely building off the more rigorous work of others, and maybe adding a few novel twists.
I think this may be a new technique to add to the Mandelboxen toolkit. But it's also possible that I've been exploring ground that's been covered before. I've only been deep diving into the Mandelbox for the last few months, so I've been playing catchup on many years of great brainstorming sessions on the forum! And looking at lots of Fragmentarium fragments and MB3D formulas for similar ideas. And there
is a set of formulas, probably best represented by MB3D's ABoxVaryShapes, that on first glance may seem similar. However, as best I can tell these all modify the calculated distance from the origin of inversion to the iterated point --
what I've labelled above as d(
OP). Whereas the shape inversion that I'm implementing modifies the distance from the origin of inversion (and following the ray
OP) to the boundary of the inversion -- d(
OS). Does anyone know of similar techniques applied to the Mandelbox?
Okay time for pictures! Here's a few from my recent experiments in Fragmentarium. To highlight how shape inversions change a 2D Mandelbox all images have the same parameters except for different shape inversions. And I hacked in an overlay to show the boundary of the shape inversions.The first image uses a standard circle inversion. The second uses an ellipse inversion. The third uses a square inversion.
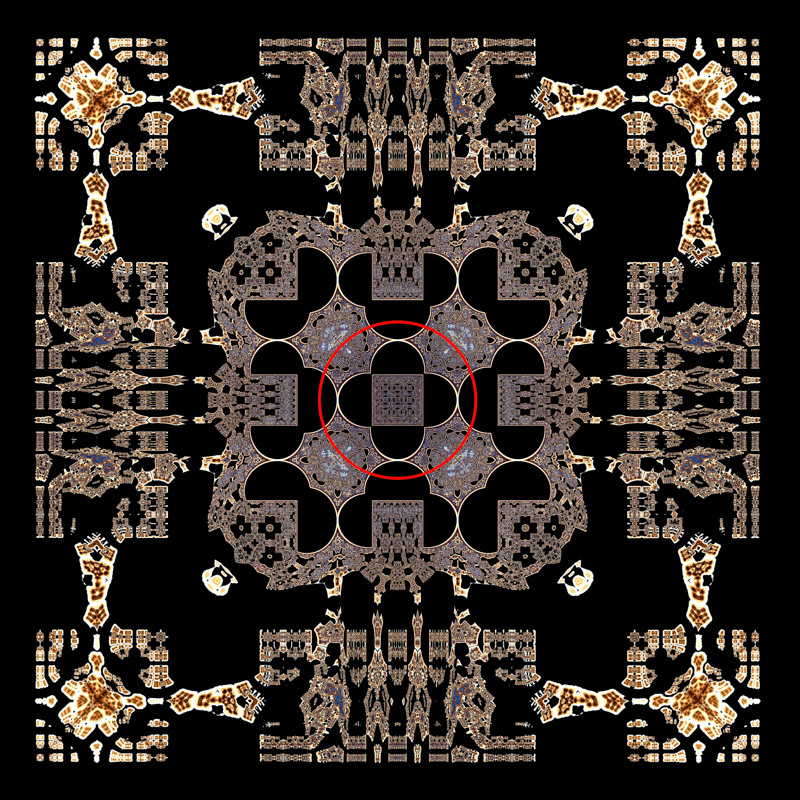


Fragmentarium frag files are in attachment. There are presets included for the images above and several more shapes.
Next step: moving to 3D shape inversions!


















