Hi
I tried to derive formula for Distance Estimator for Hypercomplex Mandendelbrot 3D and I have some conclusions.
At start I found some general theory about Distance Estimator in Wikipedia:
http://en.wikipedia.org/wiki/Mandelbrot_set. Basing at this the main problem is how to calculate derivative of hypercomplex numer. There is some strange formula:
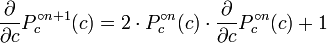
(taken from Wikipedia)
It looks terrible like some differential equation but this is only chain rule for the derivative. I used this to derive formula for iterations and I obtained following:
f'
n+1(c) = 2*f
n(c)*f'
n(c)+1 =
= 2(x + iy + jz + kw)*(dx * idy * jdz * kdw) =
re:= 2*(x*dx - y*dy - z*dz - w*dw) + 1
i:= 2*(y*dx + x*dy + w*dz + z*dw)
j:= 2*(z*dx + w*dy + x*dz + y*dw)
k:=2*(w*dx + z*dy + y*dz * x*dw)
where:
f(c) = f(x+yi+jz+kw)
f'(c) = f'(dx+idy+jdz+kdw)
first iteration should start from 1+i0+j0+k0
It looks very easy but... IT NOT WORKS PROPERLY

I made some renders and it looks very strange.
Why? The answer is very staright: we can't calculate derivative of hypercomplex numbers in that way because this numbers are not differentiable (in my opinion)
OK. Hypyercomplex - NO IDEA - but I tried with standard quaternions and it works PERFECT. In this case using the same method I obtained following formula:
re:= x*dx - y*dy - z*dz - w*dw
i:= y*dx + x*dy - w*dz + z*dw
j:= z*dx + w*dy + x*dz - y*dw
k:=w*dx - z*dy + y*dz * x*dw
first iteration also should start from 1+i0+j0+k0
I tested this and it looks on renders of slices like real Distance Estimator in every dimension.
Unfortunately I still don;t have idea how to calculate Distance Estimator for hypercomples numers.
Here's another render of the "True 3D" Mandy, rendered using my improved WIP formula for Julibrots/Quats/Hypercomplex etc. with solid based on directional distance estimation (using deltas rather than the derivative) (time 45mins @3840*2880 on a 3GHz P4HT in single-threaded mode) - max. iterations allowed was 60.
If interested you can check out how much better it is than using my older formula which was basically just solid based on iteration:
http://makinmagic.deviantart.com/art/quot-True-3D-quot-Mandelbrot-125190781David, some time ago you wrote some about using deltas instead derivatives. Could you describe what you mean? Maybe only way is use some numeric method for calculate this.
Best regards for all fractal maniacs


















