END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

Hi, i d like to propose a simple ideas to help in the way to obtain genuine 3d mandelbroot.

In short, to work with a analogue of complex number,but for a 3-signed arithmetic ,too it use 3  unities, 3 dimensions ( six real dimensions), it use a 3-signed arithmetic instead of the usual 2-signed arithmetic, and the 3 unities work in mod 9 instead of mod 4.The 3-signed arithmetic is like the einsenstein integers ( http://en.wikipedia.org/wiki/Eisenstein_integer) but with a important change of views. Well, here is my paper (in spanish):

- http://vixra.org/pdf/0911.0034v1.pdf  **pag 75

If there is interest i ll explain in simple way.

Regards

well, we begin, the n-signed arithmetics work with mods instead of signs. in mod 2, or 2 signs, it s  the 2-signed arithmetic, where if it s congruent to 1(mod 2) is negative, and if congruent to 0 (mod 2) if positive. The numbers with the same sign-values (or values of the mod ) are aditioned. In the substraction, the number with the same sign-value is aditioned, and later it is subtract to all the piles the minor number between the piles:

we abreviate   a mod b like [a¬b], but in the case of mod 2, we ll omit the 2

..1+(-5)+2+(-1)=3+(-6)=(-3)

equal to:

..[0]1+[1]5+[0]2+[1]1=[0]3+[1]6=[0](3-3)+[1](6-3)=[1]3

i forgot, in [a¬b] , a is the sign-value and b is the quantity of signs

Like you can see, it more easy with signs, but before, we extend it to 3-signs.

-In the adition: they are aditioned in piles the numbers with same sign-value and in the substraction , all the numbers with same sign-value are aditioned in piles, and after, the minor number between the piles is substract to all piles

example:

again we omit in [a¬3], but now for the 3

where  ..[0]=+ , [1]=$ , [2]=#
...

ps: kram, in the case of 3-signed arithmetic is a plane, with triangular tillings, where, every sign, is a cubic root of 1 (in the complex) , but the 3-signed algebra and generalized, n-signed algebra, it dont go by the way like extension( in the real dimension sense exactly).... too is a isomorphism of complex numbers,i ll try explain to my way..

then, now we can to advance to the tool can be posible create a kind of mandelbrot 3d:

the 3-signed arithmetic too it has posible analogs to the complex, but with 3 basis, where every number can be represented in a plane, then result a total of 6 real dimensions, with a,b,c  belong to 3-signed arithmetic:

L=a+bq+cp     where:  p^1=p         p^2=#q       p^3=#1
                                      p^4=#p      p^5=$q        p^6=$1
                                      p^7=$p       p^8=q          p^9=1

con   pq=qp=1

from notable product analog    (a+b+c) (a+#b+$c) (a+$b+#c) = a^3+b^3+c^3-3abc
we obtain the norma of this algebra     r^3= a^3+#b^3+$c^3-3abc

I wait this algebra can be a posibility to generate some kind of 3d mandelbrot.
some question, critique, failure or advise,??

regards

Kujonal, this is not a multi signed arithmetic this is an operator arithmetic with some newly defined operators. Try to be a bit more explicit about the map from the arithmetic to the 2d and 3d representation. eg how does the 2d mandelbrot formula look?

A diagram would help here. I have quickly glanced through tour pdf and it is most interestingand along the lines i thought.

my brief summary is that inthe set of transforms there are unary operators and binary operators , in general algorithms. These algorithms are procedures for iteration processes in general. The binary operators are culturally determined iterations and represent developments of the counting iteration which i refer to as "+1". +1 is the procedure or operation or algorithm. The iteration is a repeated binary: region to be transformed +1 object gives transformed region which becomes region to be transformed.

Graphically, which means also geometrically and symbolically i can reduce the above algorithm to

0 + 1=> 0^t=0

Now 0^t is normally valued in 2 main ways graphically  by a shape say @ or | or phonemically by a name say Uno, Wahed , etc. There are other ways to value it but culturally we choose or associate names from a namespace or marks from a numeralspace.

By this iteration we culturally construct the natural or counting numbers so called.  I will use to refer to those.

Now later mathematicians agreed a construction  of the integers using a unary operator called sign and a new numeral 0. Again Geometrical thinking was used to make sense of this unary operator as well as to give an intuitive feel for its effects. Sign allowed the number line and axes and vectors to develop naturally and laid the ground for the union of geomtry and algebra through the coordinate system. However as i have already pointed out geometrical thinking lay behind the construction of the integers from . The unary operation sign takes a natural numeral and transforms it to ±that natural numeral,

graphically/symbolically  

n  sign=> ±n.

We then us e these to construct by seperating all the + and counting them, and all the - and counting them. Next we place 0 in the centre of the two piles/ strands/ groups etc and rule that if we subtract from the + strand we must pass through 0 to get to the - strand. The number line follows naturally from this by iteration.

The next so called advance in number was the operator i. This is a unary operator and it act on the natural numbers to do what? Again geometrical thinking made sense of it , but for the same reason to call it an extension to the number systems and thus a number lead to many problems and generated a rich vein of marhematical invention.

The operator i is a unary operator that transforms geometrically on the plane by rotating it  anticlockwise .

the ooperator sign is a unary operator that transforms geometrically on the plane by rotating it anticlocwise .

So there are a whole class of unary operators that transform geometrically on the plane by fractions of  .

I believe that what you are describing using mod arithmetic as a set definer are these other unary operators. Using them you have to define binary operators and algorithms for transforming them to our established frameworks. However you should be able to write a programme to do this in principle.

Now the big question? How useful are they for the topics you have explored? Are they more useful than matrices or in matrices? Do they form a Lie group and thus have a use in string theory? In fact do they form a ring or group or field in combination with their binary operators?

Thinking about whether axes are fundamental to unary operators. I do not think so. I think axes are fundamental to geometry and even though euclid did not particularly mention them they are implicit in what he was describing. Their implicit nature in geometry was made explicit by algebra. This is because algebra is about the syntax and syntax forms of any ARITHMETIC and the syntax of the outcome of any manipulation / transform of that arithmetic. Because of algebra we can communicate alternative arithmetics and introduce and define new transforms as well as describe in revealing ways old arithmetic schemes.

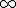
So mod(0)  define as {0,1,2,3,....} : addition and subtraction (multiple addition and multiple subtraction methods) as in everyday early centuries arithmetic.

mod(1)   define as {0} : addition and subtraction etc as in modern definition of nullity

mod(2)    define as {0,1} : addition and subtraction as in binary arithmetics and boolean algebras and modifications.

mod(3)    define as {0,1,2} : http://en.wikipedia.org/wiki/Modular_arithmetic

mod(4)    define as {0,1,2,3}

mod(5)    define as {0,1,2,3,4}                       Just in passing these sets may be useful for describing truncated iterations.

mod(6)    define as {0,1,2,3,4,5}

mod(n)    define as {0,1,2,3,.......,n-1}

All of these are algebraic definitions from which the arithmetics are prescribed for integers.

Of course we can extend this to the real numbers and then we would have formal partitioning of the reals into equivalence sets. This may be useful in describing fractal relationships at different levels, and may be what Musean numbers are attempting to describe.
Now the term number can be seen as a hangover from the historic arithmetic connection, but when these structures are aplied outside of a quantitative scheme the term number becomes misleading. So i generalise it to numeral.  

I also generalise the notion of sign to signal. IT IS EXACTLY THE SAME AS  using superscription subscription index tilde etc to distinguish a different but related denotation/ definition. In kujonai method he uses the mod set numerals as signals placing them in [], amongst other notations.

So in the case of mod(2)

define addition   0 + 0 = 0                             define multiplication      0 * 0 = 0
                       0 + 1 = 1                                                              0 * 1 = 0
                       1 + 0 = 1                                                              1 * 0 = 0  These used for logic applications.
                       1 + 1 = 0                                                              1 * 1 = 1

I will use the add definition for the signal manipulation.

write u₂, v₂ 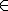   {0,1} for the general unary operator from mod(2).

 u₂ therefore has the numeral values 0 or 1.

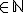
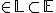
Now for any a,b  the natural numbers    or a,b   lines in  Euclidean space, a || b, a units and b units in length.
 
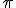
define u₂a = 0]a or 1]a                  geometrically    u₂a = a or a rotated about a point O
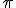
and     u₂0]a =1]a or 0]a                                      u₂a = a rotated or a
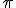
and     u₂1]a =0]a  or 1]a...                                  u₂a rotated = a or a rotated

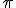
specifically

if u₂a = 0]a then u₂0]a =(u₂ + u₂)a =(0 + 0)]a

if u₂a = 1]a then u₂0]a =(u₂ + v₂)a =(1 + 0)]a

if u₂a = 0]a then u₂1]a =(u₂ + v₂)a =(0 + 1)]a

if u₂a = 1]a then u₂1]a =(u₂ + u₂)a =(1 + 1)]a
Define a binary operation for addition as follows

u₂a + v₂b                                            u₂a + v₂b = length a followed by length b

if u₂ = v₂ then = u₂(a + b)                     lengths added in direction a or in a rotated
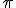
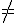
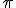
if u₂ v₂ then = u₂a + v₂b                   lengths added in opposite directions by moving in direction a followed by a rotated or vice versa

There is a procedure that collects like things together which applies in algebraic manipulation which allows the first type of addition to be applied to collections of the same types reducing any form of addition to the second type .

Kujonai now adds another rule

pick the smallest of {a,b} call it s
 Perform a binary subtraction on the numerals a,b to give a value to u₂a + v₂b

u₂a + v₂b  = u₂(a-s) + v₂(b-s)
                     = either  u₂(a-s) or v₂(b-s)

Define multiplication as follows

u₂a * v₂b  = u₂+ v₂]ab

if u₂ = v₂ then = 0]ab

if u₂ 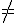v₂ then = 1]ab,

There is a logarithmic relationship to unary operators acting on each other in that apparent products have indices that are added mod(n).

So the algebraic description does not rely on axes, and so has a wider application. The signals could be tones or radio signals for example.

So why the minimum rule for subtraction in mod(3)?  And why stop when one pile is zeroed?  Why relate this to the plane as eisenstein numbers are so called complex plane coordinates not natural numerals as per your illustration?

The unary operator mod(3) would rotate an axes through so the signal is different and subtracting or adding to different piles is not the same as in mod(2) , eg 1]3 + 0]5  = 1]3-1]3 + 0]5 + 1]3 = 0]5 + 0]-3 where - is a binary operation.